LeetCode刷题——剑指offer二叉树题目汇总

系列文章目录

---

---

剑指 Offer 07. 重建二叉树(中等)

题目
输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

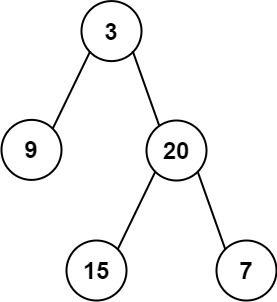
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] Output:
[3,9,20,null,null,15,7]

示例 2:

Input: preorder = [-1], inorder = [-1] Output: [-1]

限制：

0 <= 节点个数 <= 5000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof
分析
通过题目中的条件：“先序遍历”、“中序遍历”、“重建”我们可以看出来这是数据结构中经常遇到的还原树的问题。首先建立树一般使用递归的方式，我们需要考虑如何将问题转化成子问题，这个过程我们需要利用先序遍历和中序遍历的特征来进行。首先先序遍历下，第一个结点一定是根结点，右侧的所有结点都是子树结点；中序遍历在确定根结点后左侧的所有结点一定是左子树结点，右侧的结点一定是右子树节点，利用这一性质我们就可以将问题转换成子问题。

以示例1为例

先序	3（根结点）	9	20	15	7
后序	9	3（根结点）	15	20	7

后序遍历中3之前的结点为左子树结点，那么获取左子树的结点的子问题为

先序	9（根结点）
后序	9（根结点

后序遍历中3之后的结点为右子树结点，获取右子树的结点的子问题为

线序	20（根结点）	15	7
后序	15	20（根结点）	7

以此类推即可建立符合要求的树
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* buildNode(vector<int>& p, vector<int>& in, int pstart, int pend, int instart, int inend){
        TreeNode* node;
        node = new TreeNode;
        node->val = p[pstart];
        int cur;
        for(cur=instart; in[cur] != p[pstart] && cur<= inend; cur++);
        pend = pstart+1 + cur-1-instart;
        if(cur==instart){
            node->left = NULL;
        }else{
            node->left = buildNode(p, in, pstart+1, pend, instart, cur-1);
        }
        if(cur+1 > inend){
            node->right = NULL;
        }else{
            node->right = buildNode(p, in, pend+1, pend+1+inend - cur - 1, cur+1, inend);
        }
        return node;
    }
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size()==0 || inorder.size()==0){
            return NULL;
        }
        return buildNode(preorder, inorder, 0, preorder.size()-1, 0, inorder.size()-1);
    }
};

剑指 Offer 26. 树的子结构（中等）

题目
输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:
给定的树 A:

     3
    / \
   4   5
  / \
 1   2

给定的树 B：

   4 
  /
 1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false
示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true
限制：

0 <= 节点个数 <= 10000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/shu-de-zi-jie-gou-lcof

分析
这道题虽然标的是中等，但其实很简单，简单可以分为遍历A树和遍历B树的过程。遍历A树的过程是寻找A子树的根结点和B的根结点相等的结点，A遍历到A子树的根结点与B的根结点相等的点之后进行按B树遍历（search函数），按照B树的结点遍历，并逐一对比每个结点是否与A子树的结点是否相同
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool search(TreeNode* A, TreeNode* B){
        if(A==NULL || (A->val != B->val)){
            return false;
        }
        TreeNode* h1, * h2;
        h1 = B;
        h2 = A;
        bool flag = true;
        if(B->left!=NULL){
            flag = flag & search(A->left, B->left);
        }
        if(B->right!=NULL){
            flag = flag & search(A->right, B->right);
        }
        return flag;
    }
    bool isSubStructure(TreeNode* A, TreeNode* B) {
        if(B==NULL){
            return false;
        }
        if(A==NULL && B!=NULL){
            return false;
        }
        if(A->val == B->val && search(A, B)){
            return true;
        }
        return isSubStructure(A->left, B) || isSubStructure(A->right, B);
    }
};

剑指 Offer 27. 二叉树的镜像（简单）

题目
请完成一个函数，输入一个二叉树，该函数输出它的镜像。

例如输入：

     4
   /   \
  2     7
 / \   / \
1   3 6   9

镜像输出：

     4
   /   \
  7     2
 / \   / \
9   6 3   1

示例 1：

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

限制：

0 <= 节点个数 <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof
分析
镜像的实质是将左右子树互换，那么我们可以首先生成一个新的根节点，其左子树等于右子树的镜像，右子树等于左子树的镜像。这样我们就把整棵树的镜像变成了分别求左右子树的镜像的子问题，可以使用递归解答
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */


struct TreeNode* mirrorTree(struct TreeNode* root){
    struct TreeNode* newroot, *tmp;
    if(!root){
        return NULL;
    }else{
        newroot = root;
        tmp = newroot->left;
        newroot->left = mirrorTree(newroot->right);
        newroot->right = mirrorTree(tmp);
        return newroot;
    }
}

剑指 Offer 28. 对称的二叉树（简单）

题目
请实现一个函数，用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样，那么它是对称的。

例如，二叉树 [1,2,2,3,4,4,3] 是对称的。

    1
   / \
  2   2
 / \ / \
3  4 4  3

但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的:

    1
   / \
  2   2
   \   \
   3    3

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true
示例 2：

输入：root = [1,2,2,null,3,null,3]
输出：false

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/dui-cheng-de-er-cha-shu-lcof

分析
首先我们来仔细思考一下，一个树怎么才算是对称？我们可以发现对称的树在除去根节点之后的左子树和右子树是左右对称的。为了表述方便我们把树的左子树称为A树，树的右子树称为B树，A树和B树左右对称的条件是A的根结点和B的根结点的值相同，同时A的左子树与B的右子树对称，A的右子树和B的左子树对称，这样一来我们就有了递归的定义，在写递归时注意细节和边界问题即可。
代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool check(TreeNode* A, TreeNode* B){
        if(A->val != B->val){
            return false;
        } 
        bool flag = true;
        if(A->left != NULL && B->right!= NULL){
            flag = flag & check(A->left, B->right);
        }else if(A->left!=NULL || B->right!=NULL){
            return false;
        }
        if(A->right != NULL && B->left !=NULL){
            flag = flag & check(A->right, B->left);
        }else if(A->right!=NULL || B->left!=NULL){
            return false;
        }
        return flag;
    }
    bool isSymmetric(TreeNode* root) {
        if(root==NULL){
            return true;
        }
        if(root->left!=NULL && root->right!=NULL){
            return check(root->left, root->right);
        }else if(root->left==NULL && root->right==NULL){
            return true;
        }else{
            return false;
        }
    }
};

剑指 Offer 33. 二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

    5
   / \  
  2   6 
 / \  
1   3

示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

提示：

数组长度 <= 1000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-hou-xu-bian-li-xu-lie-lcof
分析
这道题主要是根据搜索树和后序遍历的性质，根据例子可得，后序遍历先遍历左子树，后遍历右子树，也就是说，当遍历到子树根结点时，序列postorder中先有一段序列小于根结点，后有一段序列大于根结点，如果不满足这个条件则返回false
代码

class Solution {
public:
    bool verifyPostorder(vector<int>& postorder) {
        for(int i=postorder.size()-1; i >= 0; i--){
            int cur = postorder[i], minn = cur;
            for(int j=i-1; j >= 0; j--){
                minn = min(minn, postorder[j]);
                if(postorder[j] > cur && minn < cur){
                    return false;
                }
            }
        }
        return true;
    }
};

剑指 Offer 68 - I. 二叉搜索树的最近公共祖先

题目
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2
和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2
和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。 p、q 为不同节点且均存在于给定的二叉搜索树中。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof
代码
记录路径后遍历求公共祖先即可

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> get_path(TreeNode* root, TreeNode* p){
        TreeNode* cur=root;
        vector<TreeNode*> ans;
        while(cur != p){
            ans.push_back(cur);
            if(cur->val < p->val){
                cur = cur->right;
            }else if(cur->val > p->val){
                cur = cur->left;
            }else{
                break;
            }
        }
        ans.push_back(p);
        return ans;
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> path_p = get_path(root, p), path_q = get_path(root, q);
        TreeNode* ans;
        for(int i=0; i < path_p.size() && i < path_q.size(); i++){
            if(path_p[i]->val == path_q[i]->val){
                ans = path_p[i];
            }else{
                break;
            }
        }
        return ans;
    }
};