Leetcode刷题——每日一题题目汇总

系列文章目录

---

---

查找遍历

169. 多数元素

题目
给定一个大小为 n 的数组，找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：[3,2,3]
输出：3
示例 2：

输入：[2,2,1,1,1,2,2]
输出：2

进阶：

尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/majority-element

分析
如果只是暴力搜索的话无法满足进阶要求，采用“消去”的思路，这里我们用nub表示暂时的众数，cnt来作为统计。如果遍历到的数是当前的众数cnt+1，如果不是cnt-1，如果cnt为0说明之前的所有的数都被抵消过了，应该将当前的数设置为众数
代码

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int nub;
        int cnt=0;
        for(int i=0; i < nums.size(); i++){
            if(cnt==0){
                nub = nums[i];
            }
            if(nub==nums[i]){
                cnt++;
            }else{
                cnt--;
            }
        }
        return nub;
    }
};

219. 存在重复元素 II

题目
给你一个整数数组 nums 和一个整数 k ，判断数组中是否存在两个 不同的索引 i 和 j ，满足 nums[i] == nums[j] 且 abs(i - j) <= k 。如果存在，返回 true ；否则，返回 false 。

示例 1：

输入：nums = [1,2,3,1], k = 3
输出：true
示例 2：

输入：nums = [1,0,1,1], k = 1
输出：true
示例 3：

输入：nums = [1,2,3,1,2,3], k = 2
输出：false

提示：

$$\begin{gathered} 1<=nums.length<=10^5 \\ -10^9<=nums[i]<=10^9 \\ 0<=k<=105 \end{gathered}$$
来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/contains-duplicate-ii
分析
如果用暴力的方式解题就直接运用循环进行查询即可，但是我们可以用滑动窗口的方式将时间复杂度降为O(n)。

用map记录数组中的数字出现的位置，当这个数字再次出现时求一下他们位置的差值，并且更新map的值。
代码

class Solution {
public:
    bool containsNearbyDuplicate(vector<int>& nums, int k) {
        set<int> s;
        map<int, int> m;
        for(int i=0; i < nums.size(); i++){
            if(s.count(nums[i])==0){
                s.insert(nums[i]);
                m[nums[i]] = i;
            }else{
                if(i - m[nums[i]] <= k){
                    return true;
                }else{
                    m[nums[i]] = i;
                }
            }
        }
        return false;
    }
};

717. 1比特与2比特字符

有两种特殊字符：

第一种字符可以用一个比特 0 来表示
第二种字符可以用两个比特(10 或 11)来表示、
给定一个以 0 结尾的二进制数组 bits ，如果最后一个字符必须是一位字符，则返回 true 。

示例 1:

输入: bits = [1, 0, 0]
输出: true
解释: 唯一的编码方式是一个两比特字符和一个一比特字符。
所以最后一个字符是一比特字符。

示例 2:

输入: bits = [1, 1, 1, 0]
输出: false
解释: 唯一的编码方式是两比特字符和两比特字符。
所以最后一个字符不是一比特字符。

提示:

1 <= bits.length <= 1000
bits[i] == 0 or 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/1-bit-and-2-bit-characters
分析
由于题目要求最后一位为0，所以我们遍历时应该从0位到n-2位，并且如果bits[i]==1说明它是一个2位数，i应该增加2，如果bits[i]==0说明它是一个1位数，i应该增加1
代码

class Solution {
public:
    bool isOneBitCharacter(vector<int> &bits) {
        int n = bits.size(), i = 0;
        while (i < n - 1) {
            i += bits[i] + 1;
        }
        return i == n - 1;
    }
};

917. 仅仅反转字母

题目
给你一个字符串 s ，根据下述规则反转字符串：

所有非英文字母保留在原有位置。
所有英文字母（小写或大写）位置反转。
返回反转后的 s 。

示例 1：

输入：s = “ab-cd”
输出：“dc-ba”

示例 2：

输入：s = “a-bC-dEf-ghIj”
输出：“j-Ih-gfE-dCba”

示例 3：

输入：s = “Test1ng-Leet=code-Q!”
输出：“Qedo1ct-eeLg=ntse-T!”

提示

1 <= s.length <= 100
s 仅由 ASCII 值在范围 [33, 122] 的字符组成
s 不含 ‘"’ 或 ‘\’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-only-letters
分析
设置双指针，当两个指针都指向字母时发生交换
代码

class Solution {
public:
    string reverseOnlyLetters(string s) {
        int left=0, right=s.size()-1;
        while(left >= 0 && left < s.size() && !isalpha(s[left]))left++;
        while(right >= 0 && right < s.size() && !isalpha(s[right]))right--;
        // cout<
        while(left < right && left >= 0 && left < s.size() && right >= 0 && right < s.size()){
            // cout<
            char tmp = s[left];
            s[left] = s[right];
            s[right] = tmp;
            left++;
            right--;
            while(!isalpha(s[left]))left++;
            while(!isalpha(s[right]))right--;
        }
        return s;
    }
};

1725. 可以形成最大正方形的矩形数目

题目
给你一个数组 rectangles ，其中 rectangles[i] = [li, wi] 表示第 i 个矩形的长度为 li 、宽度为 wi 。

如果存在 k 同时满足 k <= li 和 k <= wi ，就可以将第 i 个矩形切成边长为 k 的正方形。例如，矩形 [4,6] 可以切成边长最大为 4 的正方形。

设 maxLen 为可以从矩形数组 rectangles 切分得到的 最大正方形 的边长。

请你统计有多少个矩形能够切出边长为 maxLen 的正方形，并返回矩形 数目 。

示例 1：

输入：rectangles = [[5,8],[3,9],[5,12],[16,5]] 输出：3
解释：能从每个矩形中切出的最大正方形边长分别是 [5,3,5,5] 。 最大正方形的边长为 5 ，可以由 3 个矩形切分得到。

示例 2：

输入：rectangles = [[2,3],[3,7],[4,3],[3,7]] 输出：3

提示：

1 <= rectangles.length <= 1000
rectangles[i].length == 2 1 <= li, wi<= 109
li != wi

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-rectangles-that-can-form-the-largest-square
代码

class Solution {
public:
    int countGoodRectangles(vector<vector<int>>& rectangles) {
        int maxn=0, cnt=0;
        for(auto &a:rectangles){
            int tmp = min(a[0], a[1]);
            if(tmp > maxn){
                maxn = tmp;
                cnt=1;
            }else if(tmp == maxn){
                cnt++;
            }
        }
        return cnt;
    }
};

排序

1996. 游戏中弱角色的数量

题目
你正在参加一个多角色游戏，每个角色都有两个主要属性：攻击 和 防御 。给你一个二维整数数组 properties ，其中 properties[i] = [attacki, defensei] 表示游戏中第 i 个角色的属性。

如果存在一个其他角色的攻击和防御等级 都严格高于 该角色的攻击和防御等级，则认为该角色为 弱角色 。更正式地，如果认为角色 i 弱于 存在的另一个角色 j ，那么 attackj > attacki 且 defensej > defensei 。

返回 弱角色 的数量。

示例 1：

输入：properties = [[5,5],[6,3],[3,6]]
输出：0
解释：不存在攻击和防御都严格高于其他角色的角色。

示例 2：

输入：properties = [[2,2],[3,3]]
输出：1
解释：第一个角色是弱角色，因为第二个角色的攻击和防御严格大于该角色。

示例 3：

输入：properties = [[1,5],[10,4],[4,3]]
输出：1
解释：第三个角色是弱角色，因为第二个角色的攻击和防御严格大于该角色。

提示：

2 <= properties.length <= 105
properties[i].length == 2
1 <= attacki, defensei <= 105

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/the-number-of-weak-characters-in-the-game
分析
按照攻击力递减，如果攻击力相同就按防御力递增排序。排序完成后从左向右遍历，记录左侧最高的防御力，如果当前防御力低于之前的防御力和攻击力即严格小，否则跟新当前的防御力和攻击力
代码

class Solution {
public:
    int numberOfWeakCharacters(vector<vector<int>>& properties) {
        sort(properties.begin(), properties.end(),[](const vector<int> a, const vector<int> b){
            return a[0]==b[0] ? a[1] < b[1] : a[0] > b[0];
        });
        int am=properties[0][0], dm=properties[0][1];
        int cnt=0;
        for(auto &p:properties){
            if(p[1] < dm){
                if(p[0] < am){
                    cnt++;
                }
            }else{
                dm = p[1];
                am = p[0];
            }
        }
        return cnt;
    }
};

字符串

3. 无重复字符的最长子串

题目
给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 

解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。
示例 2:

输入: s = "bbbbb"
输出: 1

解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。
示例 3:

输入: s = "pwwkew"
输出: 3

解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，“pwke” 是一个子序列，不是子串。
示例 4:

输入: s = ""
输出: 0

提示：

0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-substring-without-repeating-characters
分析
首先我们最容易想到的是暴力解法——三层循环遍历：前两层循环用来切分字串，即第一层循环遍历起始位置，第二次循环遍历终止位置。第三层循环用来检测是否存在重复字符

但是这样的做法会很耗时间，所以我们使用滑动窗口的方法：首先设定一个起始地点start， 然后遍历字符串，遍历时记录每个字符最晚出现位置，如果遍历到的字符的最晚出现位置在start和当前位置之间则说明该区间内出现了重复的字符，记录下当前长度，并将start移到该字符最晚出现位置之后
代码

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(s==""){
            return 0;
        }
        map<char, int> m;
        set<char> st;
        int start=0;
        int ans=0;
        int tmp=0;
        for(int i=0; i < s.size(); i++){
            if(st.count(s[i])==0){
                st.insert(s[i]);
                m[s[i]] = i;
                tmp++;
            }else{
                if(m[s[i]] >= start){
                    ans = max(ans, tmp);
                    tmp = i-m[s[i]];
                    start = m[s[i]]+1;
                    m[s[i]] = i;
                }else{
                    m[s[i]] = i;
                    tmp++;
                }
            }       
        }
        ans = max(ans, tmp);
        return ans;
    }
};

539. 最小时间差（中等）

题目
给定一个 24 小时制（小时:分钟 “HH:MM”）的时间列表，找出列表中任意两个时间的最小时间差并以分钟数表示。

示例 1：

输入：timePoints = [“23:59”,“00:00”]
输出：1
示例 2：

输入：timePoints = [“00:00”,“23:59”,“00:00”]
输出：0

提示：

2 <= timePoints <= 2 * 104
timePoints[i] 格式为 “HH:MM”

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/minimum-time-difference
分析
因为要精确到分钟，所以我们可以开辟一个数组，直接将时间转换为分钟格式（整型）即可。转换之后我们对分钟进行排序，排好序后的数组相邻两个元素之差一定小于不相邻的两个元素之差。同时还要对最后一个元素和第一个元素进行比较。
代码

class Solution {
public:
    int findMinDifference(vector<string>& timePoints) {
        int* timeStemps;
        timeStemps = new int[timePoints.size()];
        for(int i=0; i < timePoints.size(); i++){
            timeStemps[i] = (int(timePoints[i][0]-'0') * 10 + int(timePoints[i][1]-'0')) * 60 + int(timePoints[i][3]-'0') * 10 + int(timePoints[i][4]-'0');
        }
        sort(timeStemps, timeStemps+timePoints.size());
        int ans = 24 * 60;
        for(int i=1; i < timePoints.size(); i++){
            ans = min(ans, timeStemps[i] - timeStemps[i-1]);
        }
        //printf("%d %d", timeStemps[0] + 24 * 60, timeStemps[timePoints.size()-1]);
        ans = min(ans, timeStemps[0] + 24 * 60 - timeStemps[timePoints.size()-1]);
        return ans;
    }
};

1189. “气球” 的最大数量

题目
给你一个字符串 text，你需要使用 text 中的字母来拼凑尽可能多的单词 “balloon”（气球）。

字符串 text 中的每个字母最多只能被使用一次。请你返回最多可以拼凑出多少个单词 “balloon”。

示例 1：

输入：text = “nlaebolko”
输出：1

示例 2：

输入：text = “loonbalxballpoon”
输出：2

示例 3：

输入：text = “leetcode”
输出：0

提示：

1 <= text.length <= 10^4 text 全部由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-number-of-balloons
代码

class Solution {
public:
    int maxNumberOfBalloons(string text) {
        int a[5] = {0};
        for(int i=0; i < text.size(); i++){
            if(text[i] == 'b'){
                a[0]++;
            }
            if(text[i] == 'a'){
                a[1]++;
            }
            if(text[i] == 'l'){
                a[2]++;
            }
            if(text[i] == 'o'){
                a[3]++;
            }
            if(text[i] == 'n'){
                a[4]++;
            }
        }
        a[2] /= 2;
        a[3] /= 2;
        int minn = a[0];
        for(int i=0; i < 5; i++){
            minn = min(a[i], minn);
        }
        return minn;
    }
};

1447. 最简分数

题目
给你一个整数 n ，请你返回所有 0 到 1 之间（不包括 0 和 1）满足分母小于等于 n 的 最简 分数 。分数可以以 任意 顺序返回。

示例 1：

输入：n = 2
输出：[“1/2”]
解释：“1/2” 是唯一一个分母小于等于 2 的最简分数。

示例 2：

输入：n = 3
输出：[“1/2”,“1/3”,“2/3”]

示例 3：

输入：n = 4
输出：[“1/2”,“1/3”,“1/4”,“2/3”,“3/4”]
解释：“2/4” 不是最简分数，因为它可以化简为 “1/2” 。

示例 4：

输入：n = 1
输出：[]

提示：

1 <= n <= 100

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/simplified-fractions
分析
要求最简，说明分子和分母最大公约数为1。同时要注意数字和字符串的转换关系
代码

class Solution {
public:
    int gcd(int a, int b){
        if(a % b==0){
            return b;
        }
        return gcd(b, a % b);
    }
    vector<string> simplifiedFractions(int n) {
        vector<string> ans;
        for(int i=2; i <= n; i++){
            for(int j=1; j < i; j++){
                if(gcd(i, j) > 1){
                    continue;
                }
                string ch1="", ch2 = "";
                int n=j;
                while(n){
                    char ch = n % 10 + '0';
                    n /= 10;
                    ch1 = ch + ch1; 
                }
                n=i;
                while(n){
                    char ch = n % 10 + '0';
                    n /= 10;
                    ch2 = ch + ch2; 
                }
                string tmp = "";
                tmp += ch1;
                tmp += '/';
                tmp += ch2;
                ans.push_back(tmp);
            }
        }
        return ans;
    }
};

2000. 反转单词前缀

题目
给你一个下标从 0 开始的字符串 word 和一个字符 ch 。找出 ch 第一次出现的下标 i ，反转 word 中从下标 0 开始、直到下标 i 结束（含下标 i ）的那段字符。如果 word 中不存在字符 ch ，则无需进行任何操作。

例如，如果 word = “abcdefd” 且 ch = “d” ，那么你应该 反转 从下标 0 开始、直到下标 3 结束（含下标 3 ）。结果字符串将会是 “dcbaefd” 。
返回 结果字符串 。

示例 1：

输入：word = “abcdefd”, ch = “d”
输出：“dcbaefd” 解释：“d” 第一次出现在下标 3 。 反转从下标
0 到下标 3（含下标 3）的这段字符，结果字符串是 “dcbaefd” 。

示例 2：

输入：word = “xyxzxe”, ch = “z”
输出：“zxyxxe” 解释：“z” 第一次也是唯一一次出现是在下标 3 。
反转从下标 0 到下标 3（含下标 3）的这段字符，结果字符串是 “zxyxxe” 。

示例 3：

输入：word = “abcd”, ch = “z”
输出：“abcd” 解释：“z” 不存在于 word 中。
无需执行反转操作，结果字符串是 “abcd” 。

提示：

1 <= word.length <= 250 word 由小写英文字母组成 ch 是一个小写英文字母

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-prefix-of-word
代码
查找并反转即可

class Solution {
public:
    string reversePrefix(string word, char ch) {
        string ans="";
        for(int i=0; i < word.size(); i++){
            ans = word[i] + ans;
            if(ch == word[i]){
                return ans + word.substr(i+1, word.size()-i-1);
            }
        }
        return word;
    }
};

2047. 句子中的有效单词数

题目
句子仅由小写字母（‘a’ 到 ‘z’）、数字（‘0’ 到 ‘9’）、连字符（’-’）、标点符号（’!’、’.’ 和 ‘,’）以及空格（’ '）组成。每个句子可以根据空格分解成 一个或者多个 token ，这些 token 之间由一个或者多个空格 ’ ’ 分隔。

如果一个 token 同时满足下述条件，则认为这个 token 是一个有效单词：

仅由小写字母、连字符和/或标点（不含数字）。
至多一个 连字符 ‘-’ 。如果存在，连字符两侧应当都存在小写字母（“a-b” 是一个有效单词，但 “-ab” 和 “ab-” 不是有效单词）。
至多一个 标点符号。如果存在，标点符号应当位于 token 的 末尾 。
这里给出几个有效单词的例子：“a-b.”、“afad”、“ba-c”、“a!” 和 “!” 。

给你一个字符串 sentence ，请你找出并返回 sentence 中 有效单词的数目 。

示例 1：

输入：sentence = "cat and  dog"
输出：3
解释：句子中的有效单词是 "cat"、"and" 和 "dog"

示例 2：

输入：sentence = "!this  1-s b8d!"
输出：0
解释：句子中没有有效单词
"!this" 不是有效单词，因为它以一个标点开头
"1-s" 和 "b8d" 也不是有效单词，因为它们都包含数字

示例 3：

输入：sentence = "alice and  bob are playing stone-game10"
输出：5
解释：句子中的有效单词是 "alice"、"and"、"bob"、"are" 和 "playing"
"stone-game10" 不是有效单词，因为它含有数字

示例 4：

输入：sentence = "he bought 2 pencils, 3 erasers, and 1  pencil-sharpener."
输出：6
解释：句子中的有效单词是 "he"、"bought"、"pencils,"、"erasers,"、"and" 和 "pencil-sharpener."

提示：

1 <= sentence.length <= 1000
sentence 由小写英文字母、数字（0-9）、以及字符（' '、'-'、'!'、'.' 和 ','）组成
句子中至少有 1 个 token

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-valid-words-in-a-sentence
代码

class Solution {
public:
    bool isValid(const string_view &word) {
        int n = word.length();
        bool has_hyphens = false;
        for (int i = 0; i < n; i++) {
            if (word[i] >= '0' && word[i] <= '9') {
                return false;
            } else if (word[i] == '-') {
                if (has_hyphens == true || i == 0 || i == n - 1 || !islower(word[i - 1]) || !islower(word[i + 1])) {
                    return false;
                }
                has_hyphens = true;
            } else if (word[i] == '!' || word[i] == '.' || word[i] == ',') {
                if (i != n - 1) {
                    return false;
                }
            }
        }
        return true;
    }

    int countValidWords(string sentence) {
        stringstream ss(sentence);
        string s;
        int cnt=0;
        while(ss>>s){
            if(isValid(s)){
                cnt++;
            }
        }
        return cnt;
    }
};

二进制

1342. 将数字变成 0 的操作次数

题目
给你一个非负整数 num ，请你返回将它变成 0 所需要的步数。 如果当前数字是偶数，你需要把它除以 2 ；否则，减去 1 。

示例 1：

输入：num = 14 输出：6 解释： 步骤 1) 14 是偶数，除以 2 得到 7 。 步骤 2） 7 是奇数，减 1 得到 6 。
步骤 3） 6 是偶数，除以 2 得到 3 。 步骤 4） 3 是奇数，减 1 得到 2 。 步骤 5） 2 是偶数，除以 2 得到 1 。
步骤 6） 1 是奇数，减 1 得到 0 。

示例 2：

输入：num = 8 输出：4 解释： 步骤 1） 8 是偶数，除以 2 得到 4 。 步骤 2） 4 是偶数，除以 2 得到 2 。 步骤
3） 2 是偶数，除以 2 得到 1 。 步骤 4） 1 是奇数，减 1 得到 0 。

示例 3：

输入：num = 123 输出：12

提示：

0 <= num <= 10^6

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-steps-to-reduce-a-number-to-zero
分析
除2相当于二进制中右移一位
代码

class Solution {
public:
    int numberOfSteps(int num) {
        int cnt=0;
        while(num){
            if(num & 1){
                num--;
            }else{
                num >>= 1;
            }
            cnt++;
        }
        return cnt;
    }
};

1763. 最长的美好子字符串

题目
当一个字符串 s 包含的每一种字母的大写和小写形式 同时 出现在 s 中，就称这个字符串 s 是 美好 字符串。比方说，“abABB” 是美好字符串，因为 ‘A’ 和 ‘a’ 同时出现了，且 ‘B’ 和 ‘b’ 也同时出现了。然而，“abA” 不是美好字符串因为 ‘b’ 出现了，而 ‘B’ 没有出现。

给你一个字符串 s ，请你返回 s 最长的 美好子字符串 。如果有多个答案，请你返回 最早 出现的一个。如果不存在美好子字符串，请你返回一个空字符串。

示例 1：

输入：s = “YazaAay” 输出：“aAa” 解释：“aAa” 是一个美好字符串，因为这个子串中仅含一种字母，其小写形式 ‘a’
和大写形式 ‘A’ 也同时出现了。 “aAa” 是最长的美好子字符串。

示例 2：

输入：s = “Bb” 输出：“Bb” 解释：“Bb” 是美好字符串，因为 ‘B’ 和 ‘b’ 都出现了。整个字符串也是原字符串的子字符串。

示例 3：

输入：s = “c” 输出："" 解释：没有美好子字符串。

示例 4：

输入：s = “dDzeE” 输出：“dD” 解释：“dD” 和 “eE” 都是最长美好子字符串。 由于有多个美好子字符串，返回 “dD”
，因为它出现得最早。

提示：

1 <= s.length <= 100 s 只包含大写和小写英文字母。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-nice-substring
分析
可以将字符串从i位置开始的字串分为大写和小写字母两种情况，每种情况用二进制表示进行遍历，如果遍历到的位置大写字母和小写字母的二进制相同，说明其大小写都存在。
代码

class Solution {
public:
    string longestNiceSubstring(string s) {
        string ans="";
        int len=0;
        for(int i=0; i < s.size(); i++){
            int upper=0;
            int lower=0;
            for(int j=i; j < s.size(); j++){
                if(islower(s[j])){
                    lower |= 1<<(s[j]-'a');
                }else{
                    upper |= 1<<(s[j]-'A');
                }
                if(lower == upper && len < j - i + 1){
                    len = j - i + 1;
                    ans = s.substr(i, j-i+1);
                }
            }
        }
        return ans;
    }
};

STL

884. 两句话中的不常见单词

题目
句子 是一串由空格分隔的单词。每个 单词 仅由小写字母组成。

如果某个单词在其中一个句子中恰好出现一次，在另一个句子中却 没有出现 ，那么这个单词就是 不常见的 。

给你两个 句子 s1 和 s2 ，返回所有 不常用单词 的列表。返回列表中单词可以按 任意顺序 组织。

示例 1：

输入：s1 = "this apple is sweet", s2 = "this apple is sour"
输出：["sweet","sour"]

示例 2：

输入：s1 = "apple apple", s2 = "banana"
输出：["banana"]

提示：

1 <= s1.length, s2.length <= 200
s1 和 s2 由小写英文字母和空格组成
s1 和 s2 都不含前导或尾随空格
s1 和 s2 中的所有单词间均由单个空格分隔

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/uncommon-words-from-two-sentences
分析
使用stringstream来划分词，使用map来统计词出现的次数
代码

class Solution {
public:
    vector<string> uncommonFromSentences(string s1, string s2) {
        vector<string> ans;
        map<string, int> a, b;
        stringstream si1(s1), si2(s2);
        string tmp;
        vector<string> ss1, ss2;
        while(si1 >> tmp){
            a[tmp]++;
            if(a[tmp] == 1){
                ss1.push_back(tmp);
            }
        }
        while(si2 >> tmp){
            b[tmp]++;
            if(b[tmp] == 1){
                ss2.push_back(tmp);
            }
        }
        for(auto s:ss1){
            if(b[s]==0 && a[s]==1){
                ans.push_back(s);
            }
        }
        for(auto s:ss2){
            if(a[s]==0 && b[s]==1){
                ans.push_back(s);
            }
        }
        return ans;
    }
};

1001. 网格照明

题目
在大小为 n x n 的网格 grid 上，每个单元格都有一盏灯，最初灯都处于 关闭 状态。

给你一个由灯的位置组成的二维数组 lamps ，其中 lamps[i] = [rowi, coli] 表示 打开 位于 grid[rowi][coli] 的灯。即便同一盏灯可能在 lamps 中多次列出，不会影响这盏灯处于 打开 状态。

当一盏灯处于打开状态，它将会照亮 自身所在单元格 以及同一 行 、同一 列 和两条 对角线 上的 所有其他单元格 。

另给你一个二维数组 queries ，其中 queries[j] = [rowj, colj] 。对于第 j 个查询，如果单元格 [rowj, colj] 是被照亮的，则查询结果为 1 ，否则为 0 。在第 j 次查询之后 [按照查询的顺序] ，关闭 位于单元格 grid[rowj][colj] 上及相邻 8 个方向上（与单元格 grid[rowi][coli] 共享角或边）的任何灯。

返回一个整数数组 ans 作为答案， ans[j] 应等于第 j 次查询 queries[j] 的结果，1 表示照亮，0 表示未照亮。

示例 1：

输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
输出：[1,0]
解释：最初所有灯都是关闭的。在执行查询之前，打开位于 [0, 0] 和 [4, 4] 的灯。第 0 次查询检查 grid[1][1]
是否被照亮（蓝色方框）。该单元格被照亮，所以 ans[0] = 1 。然后，关闭红色方框中的所有灯。

第 1 次查询检查 grid[1][0] 是否被照亮（蓝色方框）。该单元格没有被照亮，所以 ans[1] = 0
。然后，关闭红色矩形中的所有灯。

示例 2：

输入：n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
输出：[1,1]

示例 3：

输入：n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
输出：[1,1,0]

提示：

1 <= n <= 109
0 <= lamps.length <= 20000
0 <= queries.length <= 20000
lamps[i].length == 2
0 <= rowi, coli < n
queries[j].length == 2
0 <=rowj, colj < n

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/grid-illumination
分析
如果开辟一个n*n的数组然后进行模拟很显然会超时，那么我们不妨换一下思路，如果一个位置是亮的，那么他的同一行，或者同一列，或者主对角线，或者副对角线至少存在一个点亮的灯。如果要去掉一个灯，那么他所在的行，列，主副对角线上的灯都减少一个，那么我们只需存储四条线上的灯的数量以及点亮的灯的集合即可
代码

class Solution {
public:
    vector<int> gridIllumination(int n, vector<vector<int>>& lamps, vector<vector<int>>& queries) {
        vector<int> ans;
        map<int, int> row, col, dig, antdig;
        set<pair<int, int>> point;
        for(auto & lamp:lamps){
            if(!point.count({lamp[0], lamp[1]})){
                row[lamp[0]]++;
                col[lamp[1]]++;
                antdig[lamp[1] + lamp[0]]++;
                dig[lamp[1] - lamp[0]]++;
                point.insert(make_pair(lamp[0], lamp[1]));
            }      
        }
        for(auto & querie:queries){
            int x = querie[0], y = querie[1];
            if(row[x]>0||col[y]>0||antdig[x+y]>0||dig[y-x]>0){
                ans.push_back(1);
            }else{
                ans.push_back(0);
            }
            for(int i=-1; i <= 1; i++){
                for(int j=-1; j <= 1; j++){
                    if(point.count(make_pair(x+i, y+j))){
                        point.erase(make_pair(x+i, y+j));
                        row[x+i]--;
                        col[y+j]--;
                        antdig[y+j + x+i]--;
                        dig[y+j - x - i]--;
                    }
                }
            }
        }
        return ans;
    }
};

链表

2. 两数相加

题目
给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.
示例 2：

输入：l1 = [0], l2 = [0]
输出：[0]
示例 3：

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

提示：

每个链表中的节点数在范围 [1, 100] 内
0 <= Node.val <= 9
题目数据保证列表表示的数字不含前导零

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/add-two-numbers
分析
首先考虑可能出现的几种情况
1、第一个链表为空
2、第二个链表为空
3、第一个链表比第二个长
4、第二个链表比第一个长
5、两个一样长

对于前两种情况直接返回另外一个表即可，对于后两者要考虑另外一个表遍历结束后剩余的进位问题，以及表的拼接问题。对于最后一种只用考虑进位问题即可。

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */


struct ListNode* addTwoNumbers(struct ListNode* l1, struct ListNode* l2){
    struct ListNode* f1, * f2, *h=l1;
    int far=0;
    if(l1==NULL){
        return l2;
    }
    if(l2==NULL){
        return l1;
    }
    while(l1!=NULL && l2!=NULL){
        int value = l1->val + l2->val + far;
        l1->val = value % 10;
        far = value / 10; 
        f1=l1;
        f2=l2;
        l1=l1->next;
        l2=l2->next;
    }
    if(l2!=NULL){
        f1->next = l2;
        l1=f1->next;
    }
    while(l1!=NULL && far){
        int value = l1->val + far;
        l1->val = value % 10;
        far = value / 10;
        f1 = l1;
        l1=l1->next;
    }
    while(far){
        struct ListNode* p;
        p = (struct ListNode *)malloc(sizeof(struct ListNode));
        p->next = NULL;
        p->val = far % 10;
        far /= 10;
        f1->next = p;
    }
    return h;
}

树

1791. 找出星型图的中心节点

题目
有一个无向的 星型 图，由 n 个编号从 1 到 n 的节点组成。星型图有一个 中心 节点，并且恰有 n - 1 条边将中心节点与其他每个节点连接起来。

给你一个二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示在节点 ui 和 vi 之间存在一条边。请你找出并返回 edges 所表示星型图的中心节点。

示例 1：

输入：edges = [[1,2],[2,3],[4,2]]
输出：2
解释：如上图所示，节点 2 与其他每个节点都相连，所以节点 2 是中心节点。

示例 2：

输入：edges = [[1,2],[5,1],[1,3],[1,4]]
输出：1

提示：

3 <= n <= 105
edges.length == n - 1
edges[i].length == 2
1 <= ui, vi <= n
ui != vi
题目数据给出的 edges 表示一个有效的星型图

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-center-of-star-graph
代码
求结点的度即可

class Solution {
public:
    int findCenter(vector<vector<int>>& edges) {
        int n = edges.size() + 1;
        vector<int> degrees(n + 1);
        for (auto & edge : edges) {
            degrees[edge[0]]++;
            degrees[edge[1]]++;
        }
        for (int i = 1; i <= n; i++) {
            if (degrees[i] == n - 1) {
                return i;
            }
        }
        return 0;
    }
};

广度优先搜索

1020. 飞地的数量

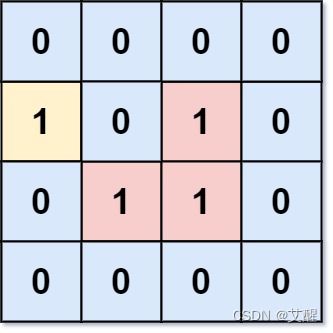
给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个海洋单元格、1 表示一个陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0包围。一个 1 没有被包围，因为它在边界上。

示例 2：

输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0 解释：所有 1 都在边界上或可以到达边界。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 500
grid[i][j] 的值为 0或 1

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-enclaves
代码
从边界开始广度优先即可

class Solution {
public:
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        queue<pair<int,int>> q;
        //cout<
        for(int i=0; i < m; i++){
            if(grid[i][0]){
                grid[i][0] = 0;
                q.push(make_pair(i, 0));
                
            }
            if(grid[i][n-1]){
                grid[i][n-1] = 0;
                q.push(make_pair(i, n-1));
                
            }
        }

        for(int i=0; i < n; i++){
            if(grid[0][i]){
                grid[0][i] = 0;
                q.push(make_pair(0, i));
            
            }
            if(grid[m-1][i]){
                grid[m-1][i] = 0;
                q.push(make_pair(m-1, i));
                
            }
        }
        
        while(!q.empty()){
            auto [x, y] = q.front();
            q.pop();
            for(int i=0; i < 4; i++){
                int tx, ty;
                tx = x + dx[i];
                ty = y + dy[i];
                if(tx >= 0 && tx < m && ty >= 0 && ty < n){
                    //cout<
                    if(grid[tx][ty]){
                        grid[tx][ty]= 0;
                    q.push(make_pair(tx, ty));
                    }
                    
                }
            }
        }
        int ans=0;
        for(int i=0; i < m; i++){
            for(int j=0; j < n; j++){
                if(grid[i][j]){
                    ans++;
                }
            }
        }
        return ans;
    }
};

1345. 跳跃游戏 IV

题目
给你一个整数数组 arr ，你一开始在数组的第一个元素处（下标为 0）。

每一步，你可以从下标 i 跳到下标：

i + 1 满足：i + 1 < arr.length
i - 1 满足：i - 1 >= 0
j 满足：arr[i] == arr[j] 且 i != j
请你返回到达数组最后一个元素的下标处所需的 最少操作次数 。

注意：任何时候你都不能跳到数组外面。

示例 1：

输入：arr = [100,-23,-23,404,100,23,23,23,3,404]
输出：3
解释：那你需要跳跃 3 次，下标依次为 0 --> 4 --> 3 --> 9 。下标 9 为数组的最后一个元素的下标。
示例 2：

输入：arr = [7]
输出：0
解释：一开始就在最后一个元素处，所以你不需要跳跃。
示例 3：

输入：arr = [7,6,9,6,9,6,9,7]
输出：1
解释：你可以直接从下标 0 处跳到下标 7 处，也就是数组的最后一个元素处。
示例 4：

输入：arr = [6,1,9]
输出：2
示例 5：

输入：arr = [11,22,7,7,7,7,7,7,7,22,13]
输出：3

提示：

1 <= arr.length <= 5 * 10^4
-10^8 <= arr[i] <= 10^8

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/jump-game-iv
分析
从题目可以看出这道题可以使用广度优先搜索解决，需要的步数就是遍历到结尾时的层数。但是这里的问题在于超时，因为直接暴力的搜索会有重复的结点访问，这一部分是可以通过剪枝优化。

因为通过暴力搜索的完整图从理论上有可能是无穷的，所以在这里为了理解方便只画图中部分的情况

如下图所示

为了解决这个问题我们可以对结点做标记，如果已经访问过则不在访问，代码中的set s和m.erase的目的都是为了移除掉已访问的结点以进行剪枝，从而优化时间
代码

struct Node{
    int idx;
    int level;
};

class Solution {
public:
    int minJumps(vector<int>& arr) {
        map<int, vector<int>> m;
        set<int> s;
        queue<Node> q;
        for(int i=0; i < arr.size(); i++){
            m[arr[i]].push_back(i);
        }
        Node n;
        n.idx = 0;
        n.level = 0;
        q.push(n);
        while(!q.empty()){
            Node p=q.front();

            q.pop();
            if(p.idx == arr.size()-1){
                return p.level;
            }
            s.insert(p.idx);
            if(m.count(arr[p.idx])){
                for(int i=0; i < m[arr[p.idx]].size(); i++){
                    if(!s.count(m[arr[p.idx]][i])){
                        Node tmp;
                        tmp.idx = m[arr[p.idx]][i];
                        tmp.level = p.level + 1;
                        q.push(tmp);
                    }
                }
                m.erase(arr[p.idx]);
            }
            
            if(p.idx > 0 && !s.count(p.idx-1)){
                Node tmp;
                tmp.idx = p.idx - 1;
                tmp.level = p.level + 1;
                q.push(tmp);
            }
            if(p.idx <= arr.size()-1 && !s.count(p.idx+1)){
                Node tmp;
                tmp.idx = p.idx + 1;
                tmp.level = p.level + 1;
                q.push(tmp);
            }
        }
        return -1;
    }
};

1765. 地图中的最高点

题目
给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由 陆地 和 水域 单元格组成的地图。

如果 isWater[i][j] == 0 ，格子 (i, j) 是一个 陆地 格子。
如果 isWater[i][j] == 1 ，格子 (i, j) 是一个 水域 格子。
你需要按照如下规则给每个单元格安排高度：

每个格子的高度都必须是非负的。
如果一个格子是是 水域 ，那么它的高度必须为 0 。
任意相邻的格子高度差 至多 为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）
找到一种安排高度的方案，使得矩阵中的最高高度值 最大 。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：

输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。

示例 2：

输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。

代码

提示：

m == isWater.length
n == isWater[i].length
1 <= m, n <= 1000
isWater[i][j] 要么是 0 ，要么是 1 。
至少有 1 个水域格子。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/map-of-highest-peak
代码

class Solution {
public:
    int mx[4] = {0, 0, 1, -1};
    int my[4] = {1, -1, 0, 0};
    vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
        int m=isWater.size(), n=isWater[0].size();
        vector<vector<int>> v(m, vector<int>(n, -1));
        queue<pair<int, int>> q;
        for(int i=0; i < m; i++){
            for(int j=0; j < n; j++){
                if(isWater[i][j]){
                    q.emplace(i, j);
                    v[i][j] = 0;
                }
            }
        }
        while(!q.empty()){
            auto &p = q.front();
            for(int i=0; i < 4; i++){
                int x = p.first+mx[i], y = p.second+my[i];
                if(x >= 0 && x < m && y >= 0 && y < n && v[x][y] == -1){
                    q.emplace(x, y);
                    v[x][y] = v[p.first][p.second]+1;
                }
            }
            q.pop();
        }
        return v;
    }
};

2045. 到达目的地的第二短时间

题目
城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [ui, vi] 表示一条节点 ui 和节点 vi 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都 同时 改变。你可以在 任何时候 进入某个节点，但是 只能 在节点 信号灯是绿色时 才能离开。如果信号灯是 绿色 ，你 不能 在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。
给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间 。

注意：

你可以 任意次 穿过任意顶点，包括 1 和 n 。
你可以假设在 启程时 ，所有信号灯刚刚变成 绿色 。

示例 1：

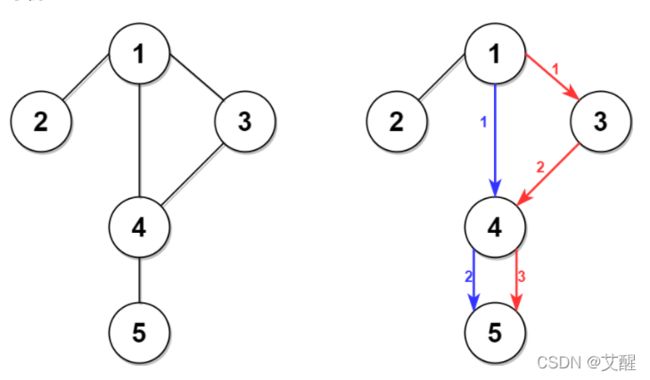
输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。   

示例 2：

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

提示：

2 <= n <= 104
n - 1 <= edges.length <= min(2 * 104, n * (n - 1) / 2)
edges[i].length == 2
1 <= ui, vi <= n
ui != vi
不含重复边
每个节点都可以从其他节点直接或者间接到达
1 <= time, change <= 103

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/second-minimum-time-to-reach-destination
分析
使用广度优先搜索获取最短距离和次短距离，这里使用path数组来表示，path[i][0]为按照最短路径的时间，path[i][1]为按照次短路径的时间，只要在广度优先遍历的时候维护最短路径和次短路径的时间即可。
代码

class Solution {
public:
    int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {
        vector<vector<int>> graph(n + 1);
        for (auto &e : edges) {
            graph[e[0]].push_back(e[1]);
            graph[e[1]].push_back(e[0]);
        }
        vector<vector<int>> path(n + 1, vector<int>(2, INT_MAX));
        path[1][0] = 0;
        queue<pair<int, int>> q;
        q.push({1, 0});
        while (!q.empty()) {
            auto [cur, timestamp] = q.front();
            q.pop();
            if(cur == n && path[cur][1] != INT_MAX){
                return path[n][1];
            }
            if (timestamp % (2 * change) >= change) {
                timestamp += (2 * change - timestamp % (2 * change));
            }
            timestamp += time;
            for (auto next : graph[cur]) {
                if (timestamp < path[next][0]) {
                    path[next][0] = timestamp;
                    q.push({next, timestamp});
                } else if (timestamp > path[next][0] && timestamp < path[next][1]) {
                    path[next][1] = timestamp;
                    q.push({next, timestamp});
                }
            }
        }
        return -1;
    }
};

深度优先搜索

1219. 黄金矿工

题目
你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

每当矿工进入一个单元，就会收集该单元格中的所有黄金。
矿工每次可以从当前位置向上下左右四个方向走。
每个单元格只能被开采（进入）一次。
不得开采（进入）黄金数目为 0 的单元格。
矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。

示例 1：

输入：grid = [[0,6,0],[5,8,7],[0,9,0]] 输出：24 解释： [[0,6,0], [5,8,7],
[0,9,0]] 一种收集最多黄金的路线是：9 -> 8 -> 7。

示例 2：

输入：grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出：28 解释：
[[1,0,7], [2,0,6], [3,4,5], [0,3,0], [9,0,20]]
一种收集最多黄金的路线是：1 -> 2-> 3 -> 4 -> 5 -> 6 -> 7。

提示：

1 <= grid.length, grid[i].length <= 15 0 <= grid[i][j] <= 100 最多 25
个单元格中有黄金。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/path-with-maximum-gold
代码
这是一道很常规的深度优先搜索题目

class Solution {
public:
    int maxn=0;
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    void dfs(vector<vector<int>>& grid, int x, int y, int cnt){
        cnt += grid[x][y];
        maxn = max(cnt, maxn);
        for(int i=0; i < 4; i++){
            int tx = x+dx[i], ty = y+dy[i];
            if(grid[tx][ty] && tx >= 0 && tx < grid.size() && ty >= 0 && ty < grid[0].size()){
                int tmp = grid[tx][ty];
                grid[tx][ty] = 0;
                dfs(grid, tx, ty, cnt);
                grid[tx][ty] = tmp;
            }
        }
    }
    int getMaximumGold(vector<vector<int>>& grid) {
        for(int i=0; i < grid.size(); i++){
            for(int j=0; j < grid[0].size(); j++){
                if(grid[i][j]!=0){
                    int tmp = grid[i][j];
                    grid[i][j] = 0;
                    
                    dfs(grid, i, j, 0);
                    grid[i][j] = tmp;
                }
            }
        }
        return maxn;
    }
};

哈希

2013. 检测正方形

题目
给你一个在 X-Y 平面上的点构成的数据流。设计一个满足下述要求的算法：

添加 一个在数据流中的新点到某个数据结构中。可以添加 重复 的点，并会视作不同的点进行处理。
给你一个查询点，请你从数据结构中选出三个点，使这三个点和查询点一同构成一个 面积为正 的 轴对齐正方形 ，统计 满足该要求的方案数目。
轴对齐正方形 是一个正方形，除四条边长度相同外，还满足每条边都与 x-轴 或 y-轴 平行或垂直。

实现 DetectSquares 类：

DetectSquares() 使用空数据结构初始化对象
void add(int[] point) 向数据结构添加一个新的点 point = [x, y]
int count(int[] point) 统计按上述方式与点 point = [x, y] 共同构造 轴对齐正方形 的方案数。

示例：

输入：

["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]

输出：

[null, null, null, null, 1, 0, null, 2]

解释：

DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // 返回 1 。你可以选择：
                               //   - 第一个，第二个，和第三个点
detectSquares.count([14, 8]);  // 返回 0 。查询点无法与数据结构中的这些点构成正方形。
detectSquares.add([11, 2]);    // 允许添加重复的点。
detectSquares.count([11, 10]); // 返回 2 。你可以选择：
                               //   - 第一个，第二个，和第三个点
                               //   - 第一个，第三个，和第四个点

提示：

point.length == 2
0 <= x, y <= 1000
调用 add 和 count 的 总次数 最多为 5000

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/detect-squares

代码

class DetectSquares {
public:
    DetectSquares() {

    }
    unordered_map<int, unordered_map<int, int>> m;
public:
    
    void add(vector<int> point) {
        int x = point[0], y = point[1];
        ++m[x][y];
    }
    
    int count(vector<int> point) {
        int ret = 0;
        int x = point[0], y = point[1];
        if(m.count(x)){
            for(auto&& [oy, c] : m[x]){
                int d = y - oy;
                if(!d) continue;
                if(m.count(x + d) && m[x+d].count(y) && m[x+d].count(oy)) ret += c * m[x+d][y] * m[x+d][oy];
                if(m.count(x - d) && m[x-d].count(y) && m[x-d].count(oy)) ret += c * m[x-d][y] * m[x-d][oy];
            }
        }
        return ret;
    }
};

/**
 * Your DetectSquares object will be instantiated and called as such:
 * DetectSquares* obj = new DetectSquares();
 * obj->add(point);
 * int param_2 = obj->count(point);
 */

动态规划

688. 骑士在棋盘上的概率

在一个 n x n 的国际象棋棋盘上，一个骑士从单元格 (row, column) 开始，并尝试进行 k 次移动。行和列是 从 0 开始 的，所以左上单元格是 (0,0) ，右下单元格是 (n - 1, n - 1) 。

象棋骑士有8种可能的走法，如下图所示。每次移动在基本方向上是两个单元格，然后在正交方向上是一个单元格。

每次骑士要移动时，它都会随机从8种可能的移动中选择一种(即使棋子会离开棋盘)，然后移动到那里。

骑士继续移动，直到它走了 k 步或离开了棋盘。

返回 骑士在棋盘停止移动后仍留在棋盘上的概率 。

示例 1：

输入: n = 3, k = 2, row = 0, column = 0
输出: 0.0625
解释:有两步(到(1,2)，(2,1))可以让骑士留在棋盘上。 在每一个位置上，也有两种移动可以让骑士留在棋盘上。骑士留在棋盘上的总概率是0.0625。

示例 2：

输入: n = 1, k = 0, row = 0, column = 0
输出: 1.00000

提示:

1 <= n <= 25
0 <= k <= 100
0 <= row, column <= n

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/knight-probability-in-chessboard
分析
为了方便表述我们先约定八个方向为方向1-8。如果k=0，则不做任何移动，此时无论起始点在哪里都一定还在棋盘上，此时概率为1。如果k=1，我们可以将问题看作起始位置方向1-8的八个（如果越界则少于八个）在k=0时的起始点在棋盘上的概率除以8（因为k=1时的起始位置可能由八个方向的任何一个点移动过来），得到这个结论之后我们打表遍历每一步每个起始位置的概率即可。
代码

class Solution {
public:
    int dx[8] = {1, 1, -1, -1, 2, -2, 2, -2};
    int dy[8] = {2, -2, 2, -2, 1, 1, -1, -1};
    double knightProbability(int n, int k, int row, int column) {
        vector<vector<vector<double>>> dp(k+1, vector<vector<double>>(n, vector<double>(n)));
        for(int step=0; step <= k; step++){
            for(int i=0; i < n; i++){
                for(int j=0; j < n; j++){
                    if(step == 0){
                        dp[step][i][j]=1;
                    }else{
                        for(int loc=0; loc < 8; loc++){
                            int tx = i + dx[loc];
                            int ty = j + dy[loc];
                            if(tx >=0 && tx < n && ty >= 0 && ty < n){
                                dp[step][tx][ty] += dp[step-1][i][j] / 8;
                            }
                        }
                    }
                }
            }
        }
        return dp[k][row][column];
    }
};

模拟

838. 推多米诺

题目
n 张多米诺骨牌排成一行，将每张多米诺骨牌垂直竖立。在开始时，同时把一些多米诺骨牌向左或向右推。

每过一秒，倒向左边的多米诺骨牌会推动其左侧相邻的多米诺骨牌。同样地，倒向右边的多米诺骨牌也会推动竖立在其右侧的相邻多米诺骨牌。

如果一张垂直竖立的多米诺骨牌的两侧同时有多米诺骨牌倒下时，由于受力平衡， 该骨牌仍然保持不变。

就这个问题而言，我们会认为一张正在倒下的多米诺骨牌不会对其它正在倒下或已经倒下的多米诺骨牌施加额外的力。

给你一个字符串 dominoes 表示这一行多米诺骨牌的初始状态，其中：

dominoes[i] = ‘L’，表示第 i 张多米诺骨牌被推向左侧，
dominoes[i] = ‘R’，表示第 i 张多米诺骨牌被推向右侧，
dominoes[i] = ‘.’，表示没有推动第 i 张多米诺骨牌。
返回表示最终状态的字符串。

示例 1：

输入：dominoes = “RR.L”
输出：“RR.L”
解释：第一张多米诺骨牌没有给第二张施加额外的力。

示例 2：

输入：dominoes = “.L.R…LR…L…”
输出：“LL.RR.LLRRLL…”

提示：

n == dominoes.length
1 <= n <= 105
dominoes[i] 为 ‘L’、‘R’ 或 ‘.’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/push-dominoes
代码

char * pushDominoes(char * dominoes){
    int left='L';
    int i=0, n=strlen(dominoes);
    while(i < n){
        int j=i; 
        while(j < n && dominoes[j]=='.'){
            j++;
        }
        char right = j < n ?dominoes[j]:'R';
        if(left==right){
            while (i < j) {
                dominoes[i++] = right;
            }
        }else if(left=='R' && right=='L'){
            int k=j-1;
            while(i < k){
                dominoes[i++]='R';
                dominoes[k--]='L';
            }
        }
        left = right;
        i=j+1;
    }
    return dominoes;
}

1380. 矩阵中的幸运数

题目
给你一个 m * n 的矩阵，矩阵中的数字 各不相同 。请你按 任意 顺序返回矩阵中的所有幸运数。

幸运数是指矩阵中满足同时下列两个条件的元素：

在同一行的所有元素中最小
在同一列的所有元素中最大

示例 1：

输入：matrix = [[3,7,8],[9,11,13],[15,16,17]]
输出：[15]
解释：15 是唯一的幸运数，因为它是其所在行中的最小值，也是所在列中的最大值。

示例 2：

输入：matrix = [[1,10,4,2],[9,3,8,7],[15,16,17,12]]
输出：[12]
解释：12是唯一的幸运数，因为它是其所在行中的最小值，也是所在列中的最大值。

示例 3：

输入：matrix = [[7,8],[1,2]]
输出：[7]

提示：

m == mat.length
n == mat[i].length
1 <= n, m <= 50
1 <= matrix[i][j]<= 10^5
矩阵中的所有元素都是不同的 通过次数22,121提交次数29,563

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/lucky-numbers-in-a-matrix
代码
打表，按照题目要求模拟即可

class Solution {
public:
    vector<int> luckyNumbers (vector<vector<int>>& matrix) {
        int m=matrix.size(), n=matrix[0].size();
        int row[m], col[n];
        for(int i=0; i < m; i++){
            row[i] = 0x5fffffff;
        }
        for(int i=0; i < n; i++){
            col[i] = 0;
        }
        for(int i=0; i < m; i++){
            for(int j=0; j < n; j++){
                row[i] = min(row[i], matrix[i][j]);
                col[j] = max(col[j], matrix[i][j]);
            }
        }
        vector<int> ans;
        for(int i=0; i < m; i++){
            for(int j=0; j < n; j++){
                if(matrix[i][j] == row[i] && row[i] == col[j]){
                    ans.push_back(matrix[i][j]);
                }
            }
        }
        return ans;
    }
};

1688. 比赛中的配对次数

题目
给你一个整数 n ，表示比赛中的队伍数。比赛遵循一种独特的赛制：

如果当前队伍数是 偶数 ，那么每支队伍都会与另一支队伍配对。总共进行 n / 2 场比赛，且产生 n / 2 支队伍进入下一轮。
如果当前队伍数为 奇数 ，那么将会随机轮空并晋级一支队伍，其余的队伍配对。总共进行 (n - 1) / 2 场比赛，且产生 (n - 1) / 2 + 1 支队伍进入下一轮。
返回在比赛中进行的配对次数，直到决出获胜队伍为止。

示例 1：

输入：n = 7
输出：6
解释：比赛详情：
- 第 1 轮：队伍数 = 7 ，配对次数 = 3 ，4 支队伍晋级。
- 第 2 轮：队伍数 = 4 ，配对次数 = 2 ，2 支队伍晋级。
- 第 3 轮：队伍数 = 2 ，配对次数 = 1 ，决出 1 支获胜队伍。
总配对次数 = 3 + 2 + 1 = 6

示例 2：

输入：n = 14
输出：13
解释：比赛详情：
- 第 1 轮：队伍数 = 14 ，配对次数 = 7 ，7 支队伍晋级。
- 第 2 轮：队伍数 = 7 ，配对次数 = 3 ，4 支队伍晋级。 
- 第 3 轮：队伍数 = 4 ，配对次数 = 2 ，2 支队伍晋级。
- 第 4 轮：队伍数 = 2 ，配对次数 = 1 ，决出 1 支获胜队伍。
总配对次数 = 7 + 3 + 2 + 1 = 13

提示：

1 <= n <= 200

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/count-of-matches-in-tournament
代码

class Solution {
public:
    int numberOfMatches(int n) {
        int cnt=0;
        while(n > 1){
            cnt += n / 2;
            n = n / 2 + n % 2;
        }
        return cnt;
    }
};

贪心

1405. 最长快乐字符串

题目
如果字符串中不含有任何 ‘aaa’，‘bbb’ 或 ‘ccc’ 这样的字符串作为子串，那么该字符串就是一个「快乐字符串」。

给你三个整数 a，b ，c，请你返回 任意一个 满足下列全部条件的字符串 s：

s 是一个尽可能长的快乐字符串。
s 中 最多 有a 个字母 ‘a’、b 个字母 ‘b’、c 个字母 ‘c’ 。
s 中只含有 ‘a’、‘b’ 、‘c’ 三种字母。
如果不存在这样的字符串 s ，请返回一个空字符串 “”。

示例 1：

输入：a = 1, b = 1, c = 7
输出：“ccaccbcc”
解释：“ccbccacc” 也是一种正确答案。

示例 2：

输入：a = 2, b = 2, c = 1
输出：“aabbc”

示例 3：

输入：a = 7, b = 1, c = 0
输出：“aabaa”
解释：这是该测试用例的唯一正确答案。

提示：

0 <= a, b, c <= 100
a + b + c > 0

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-happy-string
分析
首先从题目中我们可以看出，长度越长的串越容易造成重复字符，所以我们要尽可能的使用最长的字符串中的字符。这样问题就变成了判断选出来的字符与当前目标串的最后两个字符的关系，如果加上这个字符就已经够三个连续字符了，就选下一个次长串的字符。当完全选不出任何字符的时候终止循环即可
代码

struct Node{
    char ch;
    int num;
};
class Solution {
public:
    string longestDiverseString(int a, int b, int c) {
        string ans;
        vector<Node> v;
        Node na, nb, nc;
        na.ch = 'a', na.num = a;
        v.push_back(na);
        nb.ch = 'b', nb.num = b;
        v.push_back(nb);
        nc.ch = 'c', nc.num = c;
        v.push_back(nc);

        int cnt=0;
        while(1){
            sort(v.begin(), v.end(), [](Node a, Node b){
                return a.num > b.num;
            });
            bool flag = false;
            for(int i=0; i < v.size(); i++){
                if(v[i].num > 0 && (ans.size()==0 || ans.size()==1|| ans[ans.size()-1] != v[i].ch || ans[ans.size()-2] != v[i].ch)){
                    v[i].num --;
                    ans += v[i].ch;
                    if(v[i].num == 0){
                        cnt++;
                    }
                    flag = true;
                    break;
                }
            }
            if(!flag){
                break;
            }
        }
    
        return ans;
    }
};

1414. 和为 K 的最少斐波那契数字数目

题目
给你数字 k ，请你返回和为 k 的斐波那契数字的最少数目，其中，每个斐波那契数字都可以被使用多次。

斐波那契数字定义为：

F1 = 1
F2 = 1
Fn = Fn-1 + Fn-2 ， 其中 n > 2 。
数据保证对于给定的 k ，一定能找到可行解。

示例 1：

输入：k = 7 输出：2 解释：斐波那契数字为：1，1，2，3，5，8，13，…… 对于 k = 7 ，我们可以得到 2 + 5 = 7
。

示例 2：

输入：k = 10 输出：2 解释：对于 k = 10 ，我们可以得到 2 + 8 = 10 。

示例 3：

输入：k = 19 输出：3 解释：对于 k = 19 ，我们可以得到 1 + 5 + 13 = 19 。

提示：

1 <= k <= 10^9

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/find-the-minimum-number-of-fibonacci-numbers-whose-sum-is-k
分析
由斐波那契数列的性质可知，后面的数一定可以由前面的几个数的和组成，所以要让取的数字数量最小就要尽可能的取大的数，让k减去取得的最大的数就将问题转换成了子问题
代码

class Solution {
public:
    int findMinFibonacciNumbers(int k) {
        int cnt=0;
        vector<int> v;
        int a=1, b=1, p=1;
        v.push_back(1);
        v.push_back(1);
        while(p <= k){
            p = a + b;
            a = b;
            b=p;
            v.push_back(p);
        } 
        for(int i=v.size()-1; i >= 0; i--){
            if(v[i] <= k){
                k-= v[i];
                cnt++;
            }
        }
        return cnt;
    }
};

数学

969. 煎饼排序

题目
给你一个整数数组 arr ，请使用 煎饼翻转 完成对数组的排序。

一次煎饼翻转的执行过程如下：

选择一个整数 k ，1 <= k <= arr.length
反转子数组 arr[0…k-1]（下标从 0 开始）
例如，arr = [3,2,1,4] ，选择 k = 3 进行一次煎饼翻转，反转子数组 [3,2,1] ，得到 arr = [1,2,3,4] 。

以数组形式返回能使 arr 有序的煎饼翻转操作所对应的 k 值序列。任何将数组排序且翻转次数在 10 * arr.length 范围内的有效答案都将被判断为正确。

示例 1：

输入：[3,2,4,1]
输出：[4,2,4,3]
解释：
我们执行 4 次煎饼翻转，k 值分别为 4，2，4，和 3。
初始状态 arr = [3, 2, 4, 1]
第一次翻转后（k = 4）：arr = [1, 4, 2, 3]
第二次翻转后（k = 2）：arr = [4, 1, 2, 3]
第三次翻转后（k = 4）：arr = [3, 2, 1, 4]
第四次翻转后（k = 3）：arr = [1, 2, 3, 4]，此时已完成排序。

示例 2：

输入：[1,2,3]
输出：[]
解释：
输入已经排序，因此不需要翻转任何内容。
请注意，其他可能的答案，如 [3，3] ，也将被判断为正确。

提示：

1 <= arr.length <= 100
1 <= arr[i] <= arr.length
arr 中的所有整数互不相同（即，arr 是从 1 到 arr.length 整数的一个排列）

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/pancake-sorting

分析
煎饼排序问题找到最短解法是 NP 困难的，而且题目中要求我们找到有效答案即可。所以我们只要找到一个可行的方案即可。这里我们先查找最大的元素，以他基准反转，这样最大元素就已经放到了首位，然后以最后一位为基准反转，最大元素就到了最后一位，然后我们去掉最后一位，对最后一位之前的位数继续重复操作即可。我们以示例1中[3,2,4,1]为例，列表说明。

基准	交换后数组	最后一位
3	[4,2,3,1]	4
4	[1,3,2,4]	4
2	[3,1,2,4]	3
3	[2,1,3,4]	3
1	[2,1,3,4]	2
2	[1,2,3,4]	2

代码

class Solution {
public:
    vector<int> pancakeSort(vector<int>& arr) {
        vector<int> ans;
        for(int n=arr.size(); n > 1; n--){
            int idx = max_element(arr.begin(), arr.begin()+n) - arr.begin();
            if(idx == n - 1){
                continue;
            }
            reverse(arr.begin(), arr.begin()+idx+1);
            reverse(arr.begin(), arr.begin()+n);
            ans.push_back(idx+1);
            ans.push_back(n);
        }
        return ans;
    }
};

脑筋急转弯

1332. 删除回文子序列

题目
给你一个字符串 s，它仅由字母 ‘a’ 和 ‘b’ 组成。每一次删除操作都可以从 s 中删除一个回文 子序列。

返回删除给定字符串中所有字符（字符串为空）的最小删除次数。

「子序列」定义：如果一个字符串可以通过删除原字符串某些字符而不改变原字符顺序得到，那么这个字符串就是原字符串的一个子序列。

「回文」定义：如果一个字符串向后和向前读是一致的，那么这个字符串就是一个回文。

分析
由于只存在a和b两种字符，所以最多在第二次一定可以把字符全部删完，在字符串回文时删一次即可，不是回文时需要删两次。
代码
示例 1：

输入：s = "ababa"
输出：1
解释：字符串本身就是回文序列，只需要删除一次。

示例 2：

输入：s = "abb"
输出：2
解释："abb" -> "bb" -> "". 
先删除回文子序列 "a"，然后再删除 "bb"。

示例 3：

输入：s = "baabb"
输出：2
解释："baabb" -> "b" -> "". 
先删除回文子序列 "baab"，然后再删除 "b"。

提示：

1 <= s.length <= 1000
s 仅包含字母 ‘a’ 和 ‘b’

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/remove-palindromic-subsequences

博弈论

2029. 石子游戏 IX

题目
Alice 和 Bob 再次设计了一款新的石子游戏。现有一行 n 个石子，每个石子都有一个关联的数字表示它的价值。给你一个整数数组 stones ，其中 stones[i] 是第 i 个石子的价值。

Alice 和 Bob 轮流进行自己的回合，Alice 先手。每一回合，玩家需要从 stones 中移除任一石子。

如果玩家移除石子后，导致 所有已移除石子 的价值 总和 可以被 3 整除，那么该玩家就 输掉游戏 。
如果不满足上一条，且移除后没有任何剩余的石子，那么 Bob 将会直接获胜（即便是在 Alice 的回合）。
假设两位玩家均采用 最佳 决策。如果 Alice 获胜，返回 true ；如果 Bob 获胜，返回 false 。

示例 1：

输入：stones = [2,1]
输出：true
解释：游戏进行如下：

• 回合 1：Alice 可以移除任意一个石子。
• 回合 2：Bob 移除剩下的石子。
  已移除的石子的值总和为 1 + 2 = 3 且可以被 3 整除。因此，Bob 输，Alice 获胜。
  示例 2：

输入：stones = [2]
输出：false
解释：Alice 会移除唯一一个石子，已移除石子的值总和为 2 。
由于所有石子都已移除，且值总和无法被 3 整除，Bob 获胜。
示例 3：

输入：stones = [5,1,2,4,3]
输出：false
解释：Bob 总会获胜。其中一种可能的游戏进行方式如下：

• 回合 1：Alice 可以移除值为 1 的第 2 个石子。已移除石子值总和为 1 。
• 回合 2：Bob 可以移除值为 3 的第 5 个石子。已移除石子值总和为 = 1 + 3 = 4 。
• 回合 3：Alices 可以移除值为 4 的第 4 个石子。已移除石子值总和为 = 1 + 3 + 4 = 8 。
• 回合 4：Bob 可以移除值为 2 的第 3 个石子。已移除石子值总和为 = 1 + 3 + 4 + 2 = 10.
• 回合 5：Alice 可以移除值为 5 的第 1 个石子。已移除石子值总和为 = 1 + 3 + 4 + 2 + 5 = 15.
  Alice 输掉游戏，因为已移除石子值总和（15）可以被 3 整除，Bob 获胜。

提示：

1 <= stones.length <= 105
1 <= stones[i] <= 104

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/stone-game-ix

分析
这里将石子代表的数字转换为余数，即0、1、2，将Alice 和 Bob 设为A和B进行讨论

那么取石头的过程的两种情况是

先取1：

已取出的石子总和的3的余数	1	2	1	2	1	2	…
取出石子的过程	1	1	2	1	2	1	…

先取2：

已取出的石子总和的3的余数	2	1	2	1	2	1	…
取出石子的过程	2	2	1	2	1	2	…

可以发现无论那种情况都要先去取两次一样的石子，不考虑0的情况A赢的情况如下：
1、当1的个数为1时,2的个数大于0时A赢
2、当1的个数为2时，2的个数大于0时A赢
3、当1的个数大于等于2并且个数不大于2的个数，A赢
4、当2的个数为1时,1的个数大于0时A赢
5、当2的个数为2时，1的个数大于0时A赢
6、当2的个数大于等于2并且个数不大于1的个数，A赢
从中可以看出

A赢得条件为1的个数大于0，2的个数大于0

当0的个数为偶数，不造成影响
当0的个数为奇数相当于互换先后手，这时A赢的情况按照前面的考虑方式就会很麻烦，所以我们从表格入手，如果按照最佳的选择，那么一定是按照表格的循环进行的，因为我们要得到A赢的结果，所以我们要在循环结束之前让B取不到应取的数，再考虑0的个数是奇数，所以我们即从表中找到使得A取不到应取的数的情况即可

1、1的个数比2的个数多至少2个
2、2的个数比1的个数多至少2个
代码

class Solution {
public:
    bool stoneGameIX(vector<int>& stones) {
        int cnt[3]={0,0,0};
        for(int i=0; i < stones.size(); i++){
            cnt[stones[i]%3]++;
        }
        if(cnt[0] % 2 == 0){
            return cnt[1] >= 1 && cnt[2] >=1;
        }else{
            return cnt[1] - cnt[2] > 2 || cnt[2] - cnt[1] > 2;
        }
    }
};