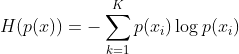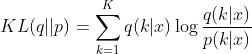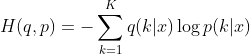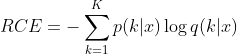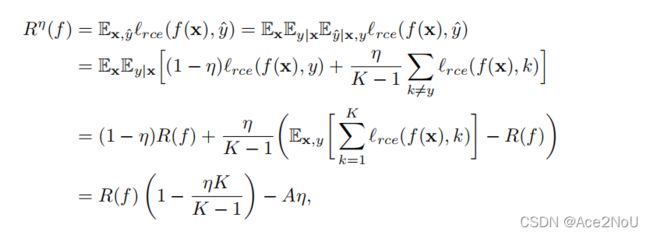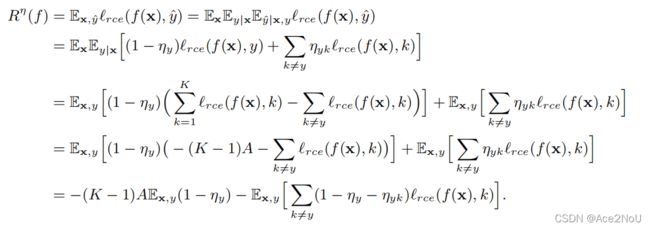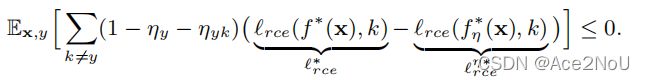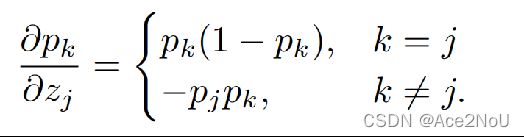【学习笔记】标签噪声下用于鲁棒性学习的对称交叉熵损失函数
这是一篇ICCV 2019的论文,论文地址:
ICCV 2019 Open Access Repository (thecvf.com)![]() https://openaccess.thecvf.com/content_ICCV_2019/html/Wang_Symmetric_Cross_Entropy_for_Robust_Learning_With_Noisy_Labels_ICCV_2019_paper.html如果访问较慢,可以尝试科学上网
https://openaccess.thecvf.com/content_ICCV_2019/html/Wang_Symmetric_Cross_Entropy_for_Robust_Learning_With_Noisy_Labels_ICCV_2019_paper.html如果访问较慢,可以尝试科学上网
目录
1.摘要
2.简介
3.相关研究
4.交叉熵的缺陷
4.1 Preliminaries 预备知识
4.2 Weakness of CE under Noisy Labels 噪声标签下CE的缺陷
5.对称交叉熵学习
5.1 Defination 对称交叉熵定义
5.2 Theoretical Analysis 理论分析
5.3 Discussion 一些讨论
6.Experiment & Code
7.Conclusion
1.摘要
在存在噪声标签的情况下训练精确的深度神经网络是一项重要而具有挑战性的任务。一般来说,用标准交叉熵(CE)损失函数训练,对简单类存在过拟合问题,对难类存在欠拟合问题。
简单类("easy" classes),指的是模型学习相对容易的类,模型很容易学习到此类的知识。
难类("hard" classes),值得是模型学习相对较难的类,模型很难学习到此类的知识。
本文提出了Symmetric Cross Entropy Learning(SL),也就是对称交叉熵学习。用逆交叉熵来增强标准交叉熵,同时解决了标准交叉熵在存在噪声标签时的欠学习和过拟合问题。
2.简介
对于在噪声标签条件下的DNN学习动力研究表明DNN对噪声标签存在过拟合问题。
一般情况下,用标准交叉熵训练深度神经网络,存在一种“类歧视”问题。即模型对于简单类收敛快,对于难类收敛更慢。在简单类开始过拟合的时候,难类有可能仍然存在欠拟合的情况。
对于这种情况,我们可以采用标签平滑正则化技术(LSR),但针对该技术的研究证明,其在难类上依然存在欠拟合。
因为,CE需要一个额外的项来学习难类,而且这个项需要具备对噪声标签的鲁棒性。
3.相关研究
目前很多人已经提出了不同的方法,以用来在标签噪声下训练DNN。它们大致可以分为三种:
- 标签校正方法
- 损失校正方法
- 精细化训练策略
标签矫正的目的是为模型的训练提供尽多正确的标签。但是这往往需要一个复杂的推理步骤来将错误的标签纠正,这个推理过程的建立依赖于一个复杂的噪声模型, 而这个模型的建立往往代价较高,或者需要一个精确的无噪声数据集。
损失矫正是通过对损失函数的修改,是的训练具有鲁棒性。常见方法有通过建模噪声转移矩阵修改损失函数,在神经网络上添加线性层增强校正结构,引导原始标签和预测标签组合,定义鲁棒损失函数,平滑标签正则化等。
精细化训练策略依赖于对训练过程的高度干预或者对训练过程超参数精确控制,为标签噪声设计全新的学习模式。导师-学生网络,联合训练策略,迭代学习框架,联合优化框架等。这使得这种方法往往具有很强的局限性,难以进行扩展应用。
4.交叉熵的缺陷
4.1 Preliminaries 预备知识
1、熵
考虑另一分类问题,对于某个样本,有![]() 种可能的分类,每一种类别都有一个分类概率
种可能的分类,每一种类别都有一个分类概率![]() 。那么,我们该分类问题熵的计算如下
。那么,我们该分类问题熵的计算如下
2、KL散度
在机器学习的情况下,如果用
代替
,通常被称为获得的信息增益。
在机器学习中,考虑一个![]() 个样本的分类问题,
个样本的分类问题,![]() 表示样本的真实标签分布,
表示样本的真实标签分布,![]() 表示模型预测的分布,
表示模型预测的分布,![]() 表示两个分布的相似性。KL散度的计算如下
表示两个分布的相似性。KL散度的计算如下
KL散度越小,两个分布之间的相似性也就越大。当![]() 和
和![]() 的分布完全一样的时候,KL散度为0,也就意味着
的分布完全一样的时候,KL散度为0,也就意味着![]() 用可以完全描述
用可以完全描述![]() ,不需要其他任何信息增益。
,不需要其他任何信息增益。
3、交叉熵
将KL散度的计算公式进行展开
在该式中,前半部分是![]() 的熵,是定值。所以我们可以只用式子的后半部分来描述两个分布之间的相似性。后半部分也叫做交叉熵。
的熵,是定值。所以我们可以只用式子的后半部分来描述两个分布之间的相似性。后半部分也叫做交叉熵。
交叉熵的计算公式如下:
4.2 Weakness of CE under Noisy Labels 噪声标签下CE的缺陷
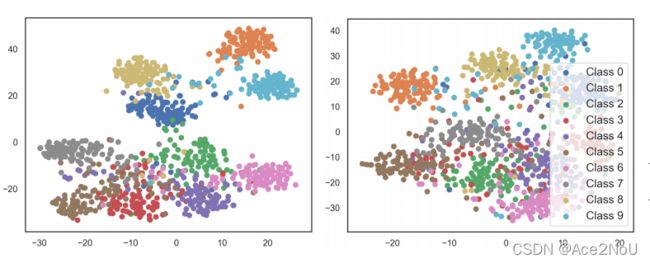
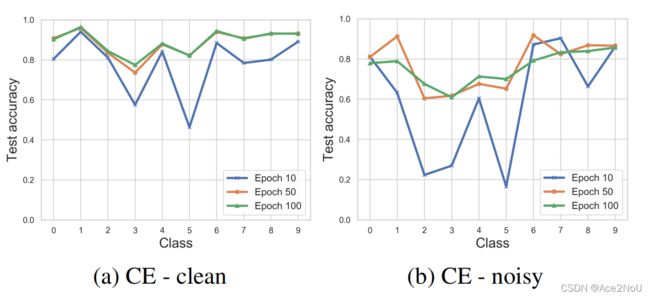
CE学习方式总是以高度“类歧视”的方法开始,即不同类在开始学习时的学习效果并不一样。在干净数据集上,最终所有类都能达到较好的学习效果,但是在含噪声数据集上不同类的正确率差异较大。
难类是学习困难的主要原因,因为这些类在特征上与其他类高度相似。
在干净数据训练中,某些类的预测置信度并不高,如下图所示,模型对第3类样本预测正确的概率不到60%。这些说明CE不足以学习难类,尤其是在带有噪声的标签情况下。
5.对称交叉熵学习
5.1 Defination 对称交叉熵定义
分类任务的目标是学习一个分类器![]() ,使得其预测的分布
,使得其预测的分布![]() 接近于真是分布
接近于真是分布![]() ,也就是最小化KL散度。考虑到有噪声情况下,
,也就是最小化KL散度。考虑到有噪声情况下,![]() 不一定代表真正的分布,
不一定代表真正的分布,![]() 反而具有一定代表性, 因此为了使
反而具有一定代表性, 因此为了使![]() 能作为真实分布,我们考虑另一个方向的KL散度,即。
能作为真实分布,我们考虑另一个方向的KL散度,即。
Symmetric KL-divergence(SKL,即对称KL散度)计算如下
从SKL的概念出发,我们可以定义对称交叉熵 Symmetric Cross Entropy (SCE)
![]()
![]()
![]()
![]() 是逆交叉熵(Reverse Cross Entropy)
是逆交叉熵(Reverse Cross Entropy)
则在样本分类任务中,新的损失函数可以定义为
![]()
其中![]() 和
和![]() 是两个超参数。
是两个超参数。![]() 用于解决
用于解决![]() 的过拟合问题,
的过拟合问题,![]() 用于调整探索
用于调整探索![]() 的鲁棒性。
的鲁棒性。
由于地实分布![]() 现在为
现在为![]() 的对数内,当标签是单热向量的时后,这可能会导致对数内的值为零。为了解决这个问题,我们定义了
的对数内,当标签是单热向量的时后,这可能会导致对数内的值为零。为了解决这个问题,我们定义了![]() (其中A<0,是一个常数)
(其中A<0,是一个常数)
5.2 Theoretical Analysis 理论分析
1、鲁棒性分析
有关在标签噪声下损失函数鲁棒性的分析的基础知识可以参考以下来自AAAI 2017的论文
[1712.09482v1] Robust Loss Functions under Label Noise for Deep Neural Networks (arxiv.org)![]() https://arxiv.org/abs/1712.09482v1
https://arxiv.org/abs/1712.09482v1
完整证明过程见:
https://openaccess.thecvf.com/content_ICCV_2019/supplemental/Wang_Symmetric_Cross_Entropy_ICCV_2019_supplemental.pdf![]() https://openaccess.thecvf.com/content_ICCV_2019/supplemental/Wang_Symmetric_Cross_Entropy_ICCV_2019_supplemental.pdf
https://openaccess.thecvf.com/content_ICCV_2019/supplemental/Wang_Symmetric_Cross_Entropy_ICCV_2019_supplemental.pdf
为了分析![]() 的鲁棒性,我们给出以下定理。
的鲁棒性,我们给出以下定理。
定理 1. 在多分类任务中,在对称噪声且噪声率
情况下, 是噪声容忍的,也称具有鲁棒性。 此外,如果
,当噪声率
的时候,
在非对称噪声和类依赖噪声下也是具有鲁棒性的,其中
。
证明:
对于对称噪声:
最后一步的得出,是由于![]() ,这是根据我们之前对逆交叉熵的定义和对
,这是根据我们之前对逆交叉熵的定义和对![]() 的定义而来。
的定义而来。
由此,我们能证明
的充分条件是![]() 。因此,在噪声率满足条件的情况下,在对称噪声下
。因此,在噪声率满足条件的情况下,在对称噪声下![]() 具有鲁棒性。
具有鲁棒性。
对于非对称和类依赖噪声:
![]() 意味着一个样本被误标记为其他任何一个类的概率均小于标记为其本身正确类的概率。也就是说混淆矩阵是对角占优的。
意味着一个样本被误标记为其他任何一个类的概率均小于标记为其本身正确类的概率。也就是说混淆矩阵是对角占优的。
此时,![]() 噪声忍耐的成立情况是
噪声忍耐的成立情况是
接下来我们证明,![]() 对于上式成立。
对于上式成立。
- 根据
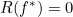 ,对于所有的
,对于所有的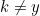 ,我们有
,我们有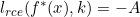 ,
,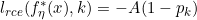 。可得
。可得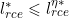 。
。 - 根据
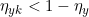 ,得到
,得到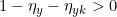 。为了是的上式成立,需要
。为了是的上式成立,需要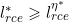 。
。 - 由此,只有
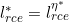 ,也就是
,也就是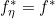
证明完成。
2、梯度分析
对![]() 进行梯度分析,有
进行梯度分析,有
得到![]() 的梯度,有
的梯度,有
在![]() 时,第二项
时,第二项![]() 是基于
是基于![]() 的自适应加速度项,在
的自适应加速度项,在![]() 时最大
时最大
在![]() 时,第二项
时,第二项![]() 是基于
是基于![]() ,在
,在![]() 处最小化概率的自适应加速度。
处最小化概率的自适应加速度。![]() 越大,加速度越大,预测越有信心。
越大,加速度越大,预测越有信心。
5.3 Discussion 一些讨论
- 改进CE的一个简单的补充方法是用一个更大的系数来加大其梯度。然而,这将导致更多的过拟合。
- MAE损失其实是RCE在A=2时的一种特殊情况。
6.Experiment & Code
本文的实验代码已经上传到了GitHub,链接:
GitHub pytorch版本![]() https://github.com/YisenWang/symmetric_cross_entropy_for_noisy_labelsGitHub打不开的同学也可以在下面的链接免费下载:图像分类鲁棒性算法对称交叉熵损失函数Python实现-深度学习文档类资源-CSDN文库
https://github.com/YisenWang/symmetric_cross_entropy_for_noisy_labelsGitHub打不开的同学也可以在下面的链接免费下载:图像分类鲁棒性算法对称交叉熵损失函数Python实现-深度学习文档类资源-CSDN文库![]() https://download.csdn.net/download/d33332/68211213
https://download.csdn.net/download/d33332/68211213
7.Conclusion
在本文中,发现了在DNN学习中使用的交叉熵(CE)的不足之处,这与难以学习的类别有关。为了解决这一问题,文章提出了对称交叉熵学习(SL),利用反向交叉熵(RCE)对称增强CE,以同时解决其欠学习和过拟合问题。文章提供了对SL的理论和经验理解。
总的来说,由于其简单和易于实现,SL是一个很有前景的训练鲁棒性的DNN对抗噪声标签的损失函数,并且是一个有吸引力的框架,可以与其他技术一起用于包含噪声标签的数据集。