LeetCode刷题——分治(python语言)
LeetCode刷题——分治(python语言)
一、分治
分治就是分而治之,对于一个复杂的问题,划分为规模较小的相同的问题(相互独立,如果不独立,最好用动态规划),以便各个击破。
典型的例子就是归并排序,现将数组不断平均划分,直到最后分为两个元素,比较大小,将求出的小规模的解合并为一个大规模的解,自底向上求出大规模问题的解。
二、刷题
2.1 将有序数组转换为二叉搜索树
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
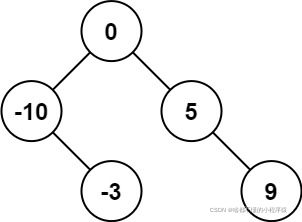
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

示例 2:
输入:nums = [1,3]
输出:[3,1]
解释:[1,3] 和 [3,1] 都是高度平衡二叉搜索树。

提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 按 严格递增 顺序排列
解法:
将二叉树的节点根据中间值划分,就不会使得左右子树的高度差大于1,根据分治法的思想解决,首先考虑递归,找到递归出口,就是节点的元素为空,返回None。否则计算中间节点,然后对左侧和右侧继续构造,组成树。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
if not nums:
return None
else:
mid = int(len(nums)/2)
return TreeNode(nums[mid],self.sortedArrayToBST(nums[:mid]),self.sortedArrayToBST(nums[mid+1:]))
2.2 从中序与后序遍历序列构造二叉树
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
示例 1:
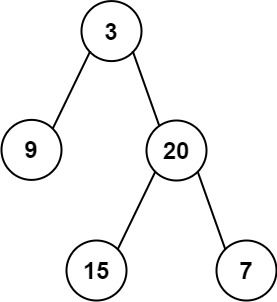
输入:inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出:[3,9,20,null,null,15,7]
示例 2:
输入:inorder = [-1], postorder = [-1]
输出:[-1]
提示:
1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由 不同 的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历
解法:
首先我们主要根据中序遍历,复现二叉树的左右节点顺序,而根据前序遍历和后序遍历,找到二叉树的根节点,这样一来,先对中序构造哈希表,这样可以有后序节点在中序的位置。func函数采用分治的策略,左右分支,相互独立,一个负责左子树,一个负责右子树,根据索引,继续构造二叉树。其中:注意鉴于后序遍历属于是左右跟,从后往前遍历,最后一个是根节点,倒数第二个是根节点的右孩子(如果有的话),所以先构造右子树。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
self.map = {j:i for i,j in enumerate(inorder)}
self.postorder = postorder
return self.func(0,len(postorder)-1)
def func(self,left,right):
if(left>right):
return None
else:
value = self.postorder.pop()
index = self.map[value]
node_right = self.func(index+1,right)
node_left = self.func(left,index-1)
return TreeNode(value,node_left,node_right)
2.3 从前序与中序遍历序列构造二叉树
给定两个整数数组 preorder 和 inorder ,其中 preorder 是二叉树的先序遍历, inorder 是同一棵树的中序遍历,请构造二叉树并返回其根节点。
示例 1:
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]
提示:
1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证 为二叉树的前序遍历序列
inorder 保证 为二叉树的中序遍历序列
解法:
方法同2.2 其中:注意鉴于先序遍历属于是左右跟,从前往后遍历,第一个元素是根节点,第二个节点是根节点的左孩子(如果有的话),所以先构造左子树。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
self.map = {j:i for i,j in enumerate(inorder)}
self.preorder = preorder
return self.func(0,len(inorder)-1)
def func(self,left,right):
if left>right:
return None
else:
value = self.preorder.pop(0)
index = self.map[value]
node_left = self.func(left,index-1)
node_right = self.func(index+1,right)
return TreeNode(value,node_left,node_right)
2.4 多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:[3,2,3]
输出:3
示例 2:
输入:[2,2,1,1,1,2,2]
输出:2
进阶:
尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。
解法一:
先构造哈希表,然后遍历数组,计数,然后最大值的索引。
class Solution:
def majorityElement(self, nums: List[int]) -> int:
map = {i:0 for i in nums}
for i in nums:
map[i] += 1
return [k for k,v in map.items() if v==max(map.values())][0]
这里附上python字典由值找键的三种方法
s = {'a':100,'b':200,'c':300}
1.print([k for k,v in s.items() if v==200])
2.b=list(s.keys())[list(s.values()).index(200)]
#将字典的值变列表,找目标下标,将键变成列表,根据刚才的下标求得值
3.new_dict={v:k for k,v in s.items()}
print(new_dict)
print(new_dict[200])
#创建新字典,在字典中查询值,但是有时候值会重复,转为字典后只有一个
s = {'a':100,'b':200,'c':300}
print(s.values())
print(s.keys())
print(list(s.values()).index(200)) # 打印值的索引
print(list(s.keys())[list(s.values()).index(200)]) # 根据列表索引取值
dict_values([100, 200, 300])
dict_keys(['a', 'b', 'c'])
1
b
原文链接:https://blog.csdn.net/weixin_43835542/article/details/104388025
解法二:
摩尔投票法:从第一个数开始count=1,遇到相同的就加1,遇到不同的就减1,减到0就重新换个数开始计数,总能找到最多的那个.
class Solution:
def majorityElement(self, nums: List[int]) -> int:
res = nums[0]
cnt = 1
for num in nums[1:]:
if(cnt == 0):
res = num
cnt += 1
elif(num != res):
cnt -= 1
else:
cnt += 1
return res