Js拓展_枚举算法

---

一、题目一

// 对序列E,X,A,M,P,L,E按字母排序，要求应用：(1)冒泡排序 (2)选择排序

1.冒泡排序

代码如下（示例）：

        //(1)冒泡排序
        var arr = ["E", "X", "A", "M", "P", "L", "E"]
        console.log("原始数据" + arr)
        var tem;
        (function () {
            for (var i = 0; i < arr.length - 1; i++) {//确定轮数
                for (var j = 0; j < arr.length - i - 1; j++) {//确定每次比较的次数
                    if (arr[j] > arr[j + 1]) {
                        tem = arr[j];
                        arr[j] = arr[j + 1];
                        arr[j + 1] = tem;
                    }
                }
            }
        })();
        function b(){
            console.log("最终排序：" + arr)
        }
        b()

2.选择排序

原理是:

1. 先将第一个数取出（ E）
2. 和第二个数比较 ，如果比他大则调换位置，反之不变（E 和 X比较，E
3. 和第三个数比较，如果比他大则调换位置，反之不变（E 和 A比较，E>A 位置调换，调换完之后数组应为 A,X,E,M,P,L,E）
4. 和第四个数比较，如果比他大则调换位置，反之不变（A 和 M比较，A
5. 一直重复上述操作，直到比完第一个数和第二个数比完

---

6. 将第二个数取出（X）
7. 和第三个数比较，如果比他大则调换位置，反之不变（X 和 E比较，X>E 位置调换，调换完之后数组应为 A,E,X,M,P,L,E）
8. 和第四个数比较，如果比他大则调换位置，反之不变（E 和 M比较，E
9. 重复上述操作，此处省略步骤。。。。。。。

// (2)选择排序
    let arr = ["E", "X", "A", "M", "P", "L", "E"]
        console.log('初始数据是：'+arr)
        function quickSort(arr) {
            for (let i = 0; i < arr.length; i++) {
                for (let j = i + 1; j < arr.length; j++) {
                    if (arr[j] < arr[i]) {
                        let t = arr[j];
                        arr[j] = arr[i];
                        arr[i] = t;
                    }
                }
                arr[i] = arr[i];
                console.log(arr[i])
            }
            return arr;
        }
        console.log('最终结果是：'+quickSort(arr))

3.快速排序

// (3)选择排序
        const arr = ["E", "X", "A", "M", "P", "L", "E"]
        console.log('初始数据是：'+arr)
        function quickSort(arr) {
            // 停止条件
            console.log(arr)
            if (arr.length <= 1) return arr;
            // 确定锚点元素
            const index = parseInt(arr.length / 2);
            // 拿到下标为index的字符
            const flagValue = arr[index];
            const leftArr = [];
            const rightArr = [];
            // 获取左右子集合
            for (let i = 0; i < arr.length; i++) {
                const item = arr[i];
                // 如果遍历的字符串下标 和 index值相等就跳过当前循环，不相等就就继续往下执行
                if (i === index) continue;
                // 如果遍历的字符串下标值小于锚点元素的值 则将此次遍历值存入左边集合中 否则则存入右边集合
                if (item <= flagValue) leftArr.push(item);
                else rightArr.push(item);
            }
            // 递归查询子集合
            return [quickSort(leftArr), flagValue, quickSort(rightArr)]
        }
        console.log('最终结果是：'+quickSort(arr))

操作要点:

1. 先取出位于数组中间的数值
2. 它左边的数先比较，比这个中间数小的用leftArr[]储存，否则用rightArr[]储存
3. 然后一直重复上述操作，直到数组长度为1时将数组直接return

在这里我当时想了很久然后选择了Debug的方式看他一步一步这么执行的
最后画了两张图，下图一和图二我给他们分别记录了各自的数组下标方便看

下图一是我在Debug控制台打印出来的数组

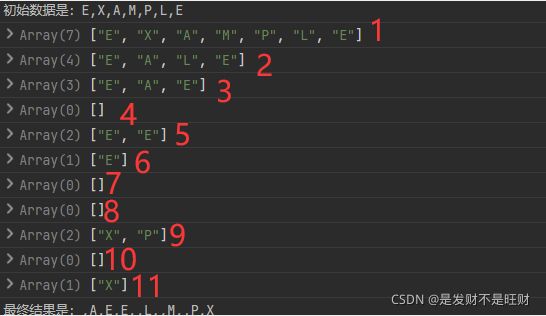
下图二是我自己画的PPT

两边的执行顺序是一一对应的，现在应该很容易看得明白了

二、题目二

//为蛮力字符串匹配写一段伪码,对于给定的模式,它能返回给定文本中所有匹配子串的数量和位置

        // 为蛮力字符串匹配写一段伪码,对于给定的模式,它能返回给定文本中所有匹配子串的数量和位置
        // 定两个字符串S和T，若T是S的子字符串，则返回T在S中的位置，否则返回-1
        // 记录T在S中返回位置的数量，并输出数量和位置
        let sum = 0;
        let cont;
        let arr = [];
        (function () {
            let s = "asdaqw2asiqweaashodoah2131qweano";
            let t = "qwea";
            let i = 0,j = 0;
            console.log(s.length)
            while (i < s.length) {
                if (s[i] === t[j]) {
                    i++;
                    j++;
                    if(j>3){
                        cont = i-j+1
                        sum++
                        arr.push(cont)
                    }
                } else {
                    i = i - j + 1;
                    j = 0;
                }
            }
        })()
        console.log("子字符串的数量是： " + sum)
        console.log("子字符串的下标是： " + arr)

三、题目三

// 用蛮力字符串匹配算法在1000个0组成的二进制文本中查找下列模式需要做多少次比较(包括成功的和不成功的）?
(1)00001 [4984]
(2)10000 [1000次]

// 具体算法
(1)00001 [共匹配4984]
1000个0 减去4个0 (末尾的0的个数小于子字符串的长度跳出循环)
再 乘 5 (子字符串的长度)
再加 4(由于末尾字符串的长度不满足余子字符串的长度，
子字符串最后只匹配的4次就跳出来循环)
=> (1000-4)*5 +4 = 4984

(2)10000 [1000次]
1000为父字符串的长度（按理来说应该只匹配了1000-4=996次 减4是因为父字符串的最后4个的字符串长度小于子字符串的长度，不满足与比较）

        // 用蛮力字符串匹配算法在1000个0组成的二进制文本中查找下列模式需要做多少次比较(包括成功的和不成功的）?
        // (1)00001 [4984]
        // 具体算法
        // 1000个0 减去4个0 (末尾的0的个数小于子字符串的长度跳出循环)
        // 再 乘 5 (子字符串的长度)
        // 再加 4(由于末尾字符串的长度不满足余子字符串的长度，子字符串最后只匹配的4次就跳出来循环)
        // => (1000-4)*5 +4 = 4984
        // (2)10000 [1000次]
        // 每一个子字符串匹配一次
        let sum = 0;
        (function () {
            let s = "00000000.....";//(共1000个)
            let t = "1000"; //t ="00001"
            let i = 0, j = 0
            console.log(s.length)
            while (i < s.length) {
                if (s[i] === t[j]) {
                    i++;
                    j++;
                } else {
                    i = i - j + 1;
                    j = 0;
                }
                sum++;
            }
        })()
        console.log("子字符串的数量是： " + sum)

四、题目四

//两个点P1(x1,y1)和P2(x2,y2)之间的距离有多种不同的定义方式。
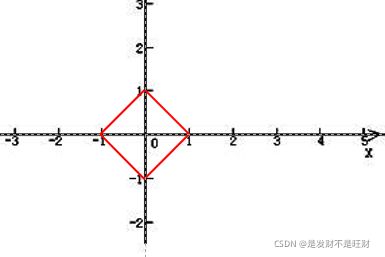
（1）在x-y坐标平面上绘出所有与原点(0,0)的曼哈顿距离等于1的点。再对欧几里得的距离dE也做一遍。
（2）对错题:最近对问题的解不依赖于用何种距离——dE或dM

题解1

在x-y坐标平面上绘出所有与原点(0,0)的曼哈顿距离等于1的点。再对欧几里得的距离dE也做一遍。

曼哈顿距离的定义：
dM(P1,P2)=︱x1-x2︱+︱y1-y2︱

答：曼哈顿距离绘图如下

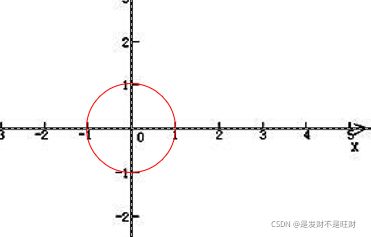
欧氏距离（欧几里得）的定义：
dE = √((x1-x2)² +(y1-y2)² )

答：欧式距离绘图如下

题解2

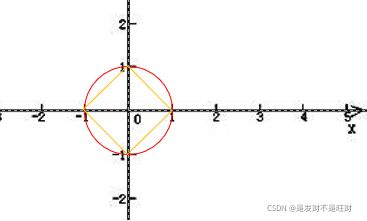
对错题:最近对问题的解不依赖于用何种距离——dE或dM
答：曼哈顿距离（这里我不太明白老师的意思，这题是我靠下图的主观判断的出来的结论）

五、题目五

//对于一个包含n个不同点的集合，它的凸包中极点的最大数量和最小数量分别会是多少?

1.凸包

1 .在一个实数向量空间V中，对于给定集合X，所有包含X的凸集的交集S被称为的凸包
2 .凸包的最左边的点和最右边的两个极点分别为凸包的最大值和最小值

2.题解

答：凸包极点最大数量为n，最小数量为3（3点组成一个面）

六、题目六

//用伪码写一个解凸包问题的蛮力算法。

function(S){
输入:n个点的集合
输出：按顺序输出凸包(S)所有的顶点
if (n<=3){
按顺序输出凸包(S)的顶点
}
else{
  for (S中的任意三点：pi，pj，pk){
    if(pi，pj，pk其中任意一i但位于其他两点与P构成的三角形之外){
       删除该点
    }
  }
  找出横坐标最小的点A和横坐标最大的点B
  将凸包S划分为直线AB上方点集上凸包SU，和直线AB下方点集下凸包SB两个部分
  将SB按很坐标递增排序，SU按横坐标递减排序
  输出SL,SB
}
}

七、第七题

//概要描述一个蛮力算法，判断一个邻接矩阵表示的连通图是否具有欧拉回路。该算法的效率类型如何?

欧拉回路：包含图的每一条边，且每条边仅出现一次的回路，就是欧拉回路。即:要求边不能重复，结点可以重复。

答：时间复杂的为O(1）

        // m为节点的数量
        // n为边的数量
        let m = 6
        let n = 6
        if (n < m) {
            console.log('不具有欧拉回路')
        } else if (m % 2 === 0) {
            if (n % 2 === 0) {
                console.log('具有欧拉回路')
            } else {
                console.log('不具有欧拉回路')
            }
        } else {
            if (n % 2 === 0) {
                console.log('不具有欧拉回路')
            } else {
                console.log('具有欧拉回路')
            }
        }

八、第八题

//考虑完备子图问题:给定一个图G和正整数k，确定该图是否包含一个大小为k的完备子图即具有k个顶点的完全子图。请为该问题设计一个穷举查找算法。

九、第九题

//考虑划分问题:给定n个实数，把它们划分为元素和尽量接近、但不相交的两个子集。
为该问题设计一个穷举查找算法，应尽量减少生成子集的数量。

let array = [2, 3, 0, 4, 2, 9]
        function getSum(total, num) {
            return total + num;
        }
        function arrayChunk() {
            let cont = 0
            let max = array.reduce(getSum)
            let min = array.reduce(getSum)
            let data = []
            let arr1 = []
            let arr2 = []
            for (let i = 1; i < array.length; i++) {
                data = array.slice(i, array.length)
                cont = data.reduce(getSum)
                let sum = max - cont
                if (Math.abs(cont - sum)<min){
                    min = Math.abs(cont - sum)
                    arr1 = data
                    arr2 = array.slice(1, i)
                }
                // min = Math.min(min,Math.abs(cont - sum))
            }
            console.log('其中分割出来的子集为：'+arr2+'和'+arr1)
            console.log('相差的最小值为：'+min)
        }