最小生成树-克鲁斯卡尔算法(Kruskal算法)
问题出发点:
对于任意一个连通网的最小生成树来说,在要求总的权值最小的情况下,最直接的想法就是将连通网中的所有边按照权值大小进行升序排序,从小到大依次选择。
条件控制
1.任意定点之间只有一条通路,不能产生环
2.对于n个顶点的生成树只有n-1条通路即可
具体思路
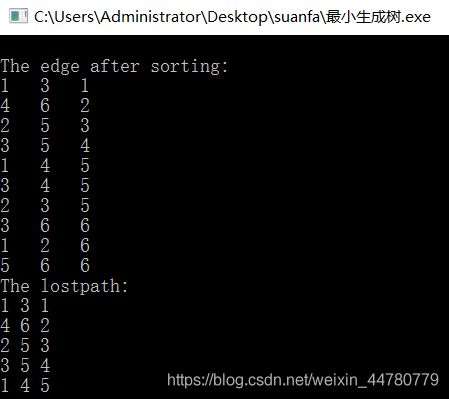
1.先将边按照边的权值排序
2.从小到大依次判断边,若加入该边不形成环,则将该边加入其中,反之,继续扫描下一条边
3.判断结束条件:加入的边为n-1条
具体实现
如何判断是否成环?
//parent[i]表示i结点在已经生成树中可到达结点;
int Find(int x){
while(parent[x]>0){
x=parent[x];
} return x;
}
void Kruskal(){
int k=0,i=0;
printf("The lostpath:\n");
while(k<n-1){
int a=Find(sortedge[i].form); //获取已经排序边表中一端点的可到达端点a
int b=Find(sortedge[i].to); //获取已经排序边表中另一端点的可到达端点b
if(a!=b){//若ab不相同,则表示不能形成换
parent[a]=b;//将a的可到达端点设为b,以便判断下一条边是否形成环
//输出加入生成树的边
printf("%d %d %d\n",sortedge[i].form,sortedge[i].to,sortedge[i].weight);
k++;
}
i++;
}
}
算法实现源码
#include