探索性数据分析(四)——特征工程(对数转换、标准化/归一化、离散化、标签编码、独热编码、Dummy变量)
前言
本篇笔记内容摘要:
特征工程的基础介绍和常用方法总结,包括对数转换、特征标准化、离散化、Label Encoder、OneHot Encoder 以及 Dummy Variables。
这系列文章大纲是基于 A Comprehensive Guide to Data Exploration 翻译搬运过来。作者在文章中比较系统地概括了EDA的内容,十分适合初学者学习。除了原作者的内容,我还整合了自己的学习笔记、以及网上找到的学习资料。
下面是之前的文章链接:
《探索性数据分析(1)—— 变量识别和分析》
《探索性数据分析(2)—— 缺失值处理》
《探索性数据分析(3)—— 异常值处理》
有任何翻译错误或内容补充,欢迎大家在评论区留言指出,欢迎一起讨论~
特征工程基本概念 Feature Engineering
什么是特征工程?
特征工程就是从现有数据中提取更多信息。没有在原始数据里添加任何信息,但实际上特征工程可以使得原有的数据更加有用。找出在数据里的隐藏信息,这种从数据中提取信息的过程称为特征工程。
广义上说,特征工程也包含了数据清洗和预处理,只要是给数据加工并提纯出信息的,都可以算是特征工程
特征工程的流程是什么?
变量转换(Variable transformation )和特征构造(Variable / Feature creation.)是两个基本的流程。
一、变量转换Variable Transformation
在数据建模中,转换是指用函数替换变量。例如,将变量x替换为平方根/立方根或对数x就是一种转换。换言之,转换是一个改变变量与其他变量的分布或关系的过程。
什么时候需要变量转换?
当变量的单位、大小、分布等等不一致或者不方便我们分析,就需特征转换:
| 情况 | 处理方法 |
|---|---|
| 1) 更改变量的比例或/标准化变量的值 | 对数转换、标准化/归一化 |
| 2) 将复杂的非线性关系转换为线性关系 | 对数转换、标准化/归一化 |
| 3)将斜分布转换为正态分布/对称分布(右偏) | 取变量的平方根/立方根或对数 |
| 4) 将斜分布转换为正态分布/对称分布(左偏) | 取变量的平方/立方或指数 |
| 5) 按业务经验需要转换变量 | 使用Binning按需要分组 |
1)对数(Logarithm)
对数变量是一种常用的转换方法,
- 通常用于减少变量的右偏态。
- 不能应用于零值或负值。
2)平方/立方根(Square / Cube root)
变量的平方、立方、平方根、立方根、指数函数也是用于改变变量的分布。然而,它没有对数变换那么重要。
- 平方:处理左偏分布,放大特征变量,应用于包括零的正值。
- 立方:处理左偏分布,放大特征变量,应用于包括零的负值。
- 平方根:处理右偏分布,缩小特征变量,应用于包括零的正值。
- 立方根:处理右偏分布,缩小特征变量,立方根可以应用于包括零的负值。
使用时注意原始数值范围是否小于1/-1,则平方和平方根的作用相反。例如 0. 5 2 = 0.25 \ 0.5^{2} = 0.25\, 0.52=0.25。
3)分类技术(Binning)
用于对变量进行分类,可以直接对变量原始值、百分比或频率执行。
一般是根据经验选择适合的分类区间。例如:把收入分成高、中、低三类;把学历分成高学历(大学、研究生、博士)和低学历(初中、高中)。
或者直接按分位数来划分区间,将数据分成几等份。
4)特征标准化:
什么时候需要特征标准化
标准化主要是针对数值特征,将杂乱的数据整理好,更便于分析建模。
比如:特征数量级不一致。比如特征A是以万为单位(9W、6W、15W), 而特征B在[0-100]的区间里,两个特征大小不一致就会影响算法的结果。比如逻辑回归、KNN、聚类等距离计算。
特征缩放经验:
如果特性不是高斯型的,例如,有一个倾斜分布或有异常值,我们可以将特征转换为高斯类(用对数/平方/立方),然后使用规范化-标准化。
a) 标准化 (Standard Scaler)
- 公式:Standard Scaler x i − μ σ \frac{x_i - \mu}{\sigma} σxi−μ
- 使样本数据的分布接近均值为0,标准差为1的正态分布,
- 在执行距离或协方差计算时(聚类、PCA和LDA等算法),最好采用标准化,因为它将消除尺度对方差和协方差的影响
b) 归一化(Min-Max Scaler)
- 公式:Min-Max Scaler x i − m i n ( x ) m a x ( x ) − m i n ( x ) \frac{x_i - min(x)}{max(x) - min(x)} max(x)−min(x)xi−min(x)
- 将特征缩放到[0,1]中间
- 只适合特定范围内分布的情况,如果最小值和最大值发生变化,就会影响最后结果。
其他归一化方法:
- Maxabs 归一化: 公式: x i m a x ( x ) \frac{x_i}{max(x) } max(x)xi, 以最大值为标准1,将特征缩放到[-1,1]之间。
- Mean归一化:公式: x i − m e a n ( x ) m a x ( x ) − m i n ( x ) \frac{x_i - mean(x)}{max(x) - min(x)} max(x)−min(x)xi−mean(x),将特征缩放到[-1,1]中间,将数据分布中心移到原点.
c) Robust Scaler
- 公式:Robust Scaler x i − m e d i a n ( x ) I Q R ( 1 , 3 ) ( x ) \frac{x_i - median(x)}{IQR_{(1,3)}(x)} IQR(1,3)(x)xi−median(x)
- 不会处理结果中移除异常值,因此可以保持数据整体情况。
- 适合有许多异常值的数据集。
代码例子
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler, MaxAbsScaler
import numpy as np
import pandas as pd
np.set_printoptions(suppress=True)
#导入数据
views = pd.DataFrame([-100,-1000,1295., 25., 19000., 5., 1., 300.], columns=['views'])
#z-score标准化
views['zscore'] = StandardScaler().fit_transform(views[['views']])
#归一化-Minmax
views['minmax'] = MinMaxScaler().fit_transform(views[['views']])
#归一化-Maxabs
views['Maxabs']=MaxAbsScaler().fit_transform(views[['views']])
#Robust Scaling
views['robust'] = RobustScaler().fit_transform(views[['views']])
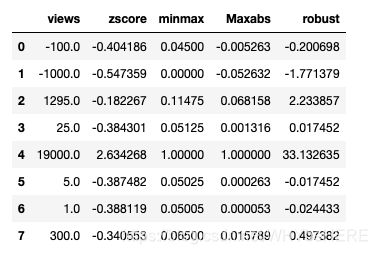
#查看结果
views
归一化和标准化的区别: 参考文章链接
5) 离散化
为什么要离散化
通过将具有相似预测能力的相似属性分组,帮助提高模型性能。离散化的特征相对于连续型特征更易理解,大大降低异常值的影响,降低过拟合。
我自己的理解是:将一个范围内的连续性特征,也就是一堆数字,转换成了几个特定的分组。比如月收入0到100W,直接转换成低、中、高收入三组,使用三个类别替代了具体的收入数值,这样更容易理解,也减少了算法的时间。同时也排出了大部分异常值的干扰,像是超高收入的1000W也直接归类到了‘高收入’组里。
离散化方法
一般情况下,离散化方法没有最佳选择,主要取决于特征的含义和使用的算法。常见的方法有:
- 根据数值范围分组,如分位数切分
- 根据频率分组
- K-means 聚类分组
- 决策素分组
代码例子
接着用上面的views数据,这里用最简单的离散化方法binning特征:
#自定义范围分组
bins=[-2000,0,2000,20000] #这个数要自己定
group=['小于0','2000以下','大于2000'] #标签名字
views['bin_labels'] =pd.cut(views['views'],bins,labels=group) #打标签
#分为数切分
quantile_list = [0, .25, .5, .75, 1.] #找出5个切分点
quantiles = views['views'].quantile(quantile_list) #找到具体切分的数字
quantile_labels = ['0-25Q', '25-50Q', '50-75Q', '75-100Q'] #标签值
views['viewslabels'] = pd.qcut(views['views'],q=quantile_list,labels=quantile_labels) #打标签分组
views
6)LabelEncoder 和 OneHotEncoder
a)标签编码(LabelEncoder)
将分类变量每一种类别都转换为一种数字格式。
Data = pd.DataFrame(['红', '橙', '黄', '绿', '青', '绿','绿' ,'红'], columns=['A'])
#方法一:LabelEncoder
from sklearn.preprocessing import LabelEncoder
Data['A_labels'] = LabelEncoder().fit_transform(Data['A'])
#查看LabelEncoder具体标签
gle = LabelEncoder()
genre_labels = gle.fit_transform(Data['A'])# 将要转换的离散值的那一列传进来
genre_mappings = {index: label for index, label in enumerate(gle.classes_)}
genre_mappings
#方法二:用map操作, 自定数字标签
gen_ord_map = {'红': 1, '橙': 2, '黄': 3, '绿': 4, '青': 5} #自己写个字典
Data['A_map'] = Data['A'] .map(gen_ord_map) # 用map对目标离散值进行操作
#查看结果
Data
b)独热编码(OneHotEncoder)
将离散型特征的每一种取值都看成一种状态,比如上面的例子,颜色中有5种状态:红橙黄绿青。1表示状态激活,0表示没有激活,则红色为:01000
注:数字从0开始,顺序为{0: ‘橙’, 1: ‘红’, 2: ‘绿’, 3: ‘青’, 4: ‘黄’}
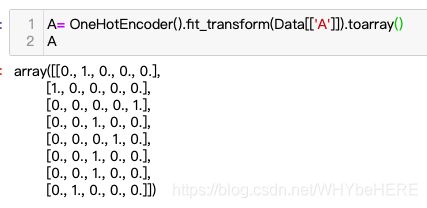
A= OneHotEncoder().fit_transform(Data[['A']]).toarray()
A
二、特征构造
什么是特征构造?
是基于现有变量生成新特征的过程。例如,我们在数据集中使用日期(dd-mm-yy)作为输入变量。我们可以生成新的变量,如日、月、年、周等等。
1)构建派生变量(Creating derived variables)
这是指使用一组函数或不同的方法从现有变量中创建新变量。
比如,在泰坦尼克号项目中,变量age有缺失值。为了预测处理缺失值,我们可以使用称呼(Master,Mr,Miss,Mrs)作为一个新变量,再计算不同称呼的平均年龄,根据称呼这个变量,对Age的缺失值进行插补。又比如,之前提及的对时间特征的信息提取,这又是另外一个重点问题了,这里先不多写。
如何决定要创建哪个变量?
这取决于分析师对业务的理解以及他对问题的一套假设。也可以使用记录变量、分块变量和其他变量转换方法来创建新的变量。
2)构建虚拟变量(Creating dummy variables)
虚拟变量,也叫哑变量。创建虚拟变量的过程,有时也叫特征的Dummy化。
在统计模型中,将分类变量作为预测因子是很有用的。分类变量的值可以是0和1。让我们以一个变量“性别”为例。我们可以产生两个变量,即值为1(男性)和0(无男性)的“Var_男性”和值为1(女性)和0(无女性)的“Var_女性”。我们还可以为两个以上的类别变量创建虚拟变量,其中包含n个或n-1个虚拟变量。

OneHot Encoder 和 Dummy Variables 的区别:
| OneHot N个特征 | Dummy(N-1)个特征 |
|---|---|
 |
 |
OneHot和Dummy的区别:参考文章链接
代码汇总
#对数转换
train['要转换的那列数']=np.log(train['要转换的那列数'])
#Bin
#自定义范围分组
bins=[-2000,0,2000,20000] #这个数要自己定
group=['小于0','2000以下','大于2000'] #标签名字
views['bin_labels'] =pd.cut(views['views'],bins,labels=group) #打标签
#分为数切分
quantile_list = [0, .25, .5, .75, 1.] #找出5个切分点
quantiles = views['views'].quantile(quantile_list) #找到具体切分的数字
quantile_labels = ['0-25Q', '25-50Q', '50-75Q', '75-100Q'] #标签名
views['viewslabels'] = pd.qcut(views['views'],q=quantile_list,labels=quantile_labels) #打标签分组
#LabelEncoder
Data['A_labels'] = LabelEncoder().fit_transform(Data['A'])
#OneHot
A= OneHotEncoder().fit_transform(Data[['A']]).toarray()
#Dummy
pd.get_dummies(Data['color']) #对指定变量dummy化,
pd.get_dummies(Data) #对数据集中所有变量
##Dummy其他参数
pd.get_dummies(Data['color'],drop_first= True,prefix_sep = '——',prefix = '列名前缀') #drop_first是否要删掉第一维数据,prefix_sep是指定分隔符号
参考链接:
A Comprehensive Guide to Data Exploration
OneHot和Dummy的区别
归一化和标准化的区别