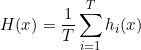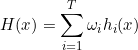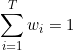机器学习之集成学习：bagging、boosting和stacking

目录

一、什么是集成学习

二、bagging 

三、boosting（提升）

四、集成学习的结合

4.1、学习器结合的好处

4.2、结合策略

4.2.1、平均法

4.2.2、投票法

4.2.3、学习法

---

一、什么是集成学习

集成学习，顾名思义就是将多个学习器结合起来以完成学习任务的一种学习思想。俗话说，三个臭皮匠，顶一个诸葛亮，集成学习就是运用了这种思想。一个模型的结果存在一定的随机性，那么就采用多个模型来抵消这种随机性，大家都说好才是真的好。所以理论上集成学习的思想可以提高模型的性能。

以分类任务为例，我们可以训练m个分类器，每个分类器可以采用相同的算法，也可以采用不同的算法。如果每个分类器均选择决策树算法，那么这个集成学习算法就叫做随机森林。各个分类器之间可以有联系，也可以没有联系。如果没有联系，称为bagging思想，如果有联系，称为boosting（提升）。

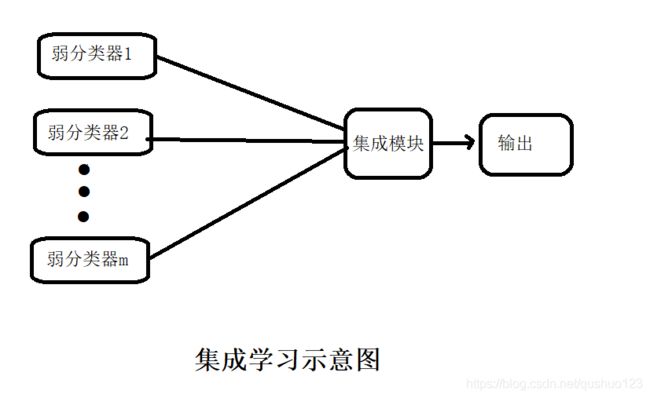
集成学习思想运用在分类中的示意图如下：

如上图所示，我们经常把个体学习器称为弱分类器， 这里的弱主要是相对于集成后的分类器来说，效果更弱一些。但集成后的分类器的性能只是在理论上更好，实际中也存在效果变差的情况，当然这只是少数。

对于集成后分类器的性能，假设我们训练了三个二分类器，集成模块采用的是少数服从多数的投票法（voting）产生，那么可能产生以下的集成结果：

因此，要想让集成后性能有所提升，个体学习器应该“好而不同”，即个体学习器要要有一定的准确性，并且应该有“多样性”，各个学习器之间有差异。 

二、bagging 

 我们已经知道，要想集成后性能提升，最好要个体学习器之间有差异。对于给定的数据集，怎样才能使差异尽可能的大呢？一种可能的做法是对训练样本进行采样，差生若干个不同的子集，从每个子集中训练出一个个体学习器。但我们又不能让每个个体学习器之间差异过大，假如每个个体学习器只学到了一小部分数据，虽然做到了不同，但没有做到好，所以最终集成后效果也不会太理想。为了解决这个问题，我们采用了自主采样法（bootstrap sampling）。

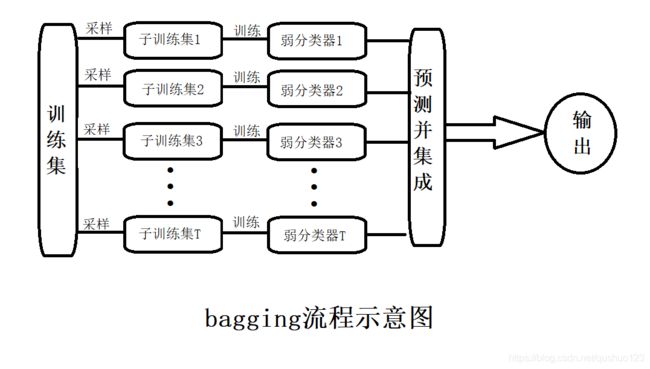
bagging是并行式集成学习的著名代表，它基于自助采样法，在给定的数据集中，每次有放回的随机取出m个数据，这样有的数据会被采样到，有的则不会，经过证明，初始训练集中约有63.2%的数据出现在采样集中。然后我们重复进行T次，就可以得到T个子集，每个子集有m个数据，对每个子集训练一个基学习器，然后将基学习器集成，这就是bagging的基本流程。

从偏差—方差的角度来看，bagging更关注于降低方差，因此它在不剪枝的决策树、神经网络等易受样本样本扰动的学习器上应用效果更为明显。bagging有一个典型的应用便是随机森林（Random Forest简称RF），我们将在后面的博客中介绍。

下面我们介绍一个bagging的示例程序：鸢尾花数据集的分类

首先导入库和数据、划分训练集与测试集，为了让效果提升更为明显，所以只采用前两个特征，四个特征都采用的话，基分类器的准确率也会很高。

# 导入算法包以及数据集
from sklearn import neighbors
from sklearn import datasets
from sklearn.ensemble import BaggingClassifier
from sklearn import tree
from sklearn.model_selection import train_test_split
import numpy as np
import matplotlib.pyplot as plt

iris = datasets.load_iris()
x_data = iris.data[:,:2]
y_data = iris.target

x_train,x_test,y_train,y_test = train_test_split(x_data, y_data)

 用KNN和决策树进行预测并打印得分：

knn = neighbors.KNeighborsClassifier()
knn.fit(x_train, y_train)
print("KNN模型得分：",knn.score(x_test, y_test))


dtree = tree.DecisionTreeClassifier()
dtree.fit(x_train, y_train)
print("决策树模型得分：",dtree.score(x_test, y_test))

结果：

采用bagging方式后：

bagging_knn = BaggingClassifier(knn, n_estimators=100)#100个弱分类器
bagging_knn.fit(x_train, y_train)

bagging_tree = BaggingClassifier(dtree, n_estimators=100)
bagging_tree.fit(x_train, y_train)

print("bagging_knn的得分为：",bagging_knn.score(x_test, y_test))
print("bagging决策树的得分为：",bagging_tree.score(x_test, y_test))

 结果:

可以看到性能其实是有所提升的，但这是我多次实验的结果，还有一些是性能不变的，甚至性能变差的，主要原因还是数据量太小，不能使各个弱分类器差异太大，数据量大时，性能提升可能就会比较明显。

三、boosting（提升）

Boosting是一族可以将弱学习器提升为强学习器的算法。这族算法的工作机制类似：先从初始训练集中训练出一个基学习器，再根据基学习器的表现对训练样本的分布进行调整，使之前学习错误的样本在后续的训练中受到更大的关注，分配更多的选择权重，基于此次调整训练下一个分类器，如此重复直至达到要求。

boosting族的经典算法有：adaboost、GBDT、XGBoost等，我们在后面的博客再一一详细介绍。

四、集成学习的结合

4.1、学习器结合的好处

1、从统计学的方面来看，由于学习任务的假设空间很大，可能有多个学习器在在训练集上达到同等的性能，此时若使用单个学习器可能因为误差导致泛化能力不佳，多个学习器集成则可以降低这一风险。

2、从计算的方面来看，学习算法都有可能陷入局部极小值，分类器也不例外。单个学习器陷入局部极小值后可能会对泛化带来的伤害是不能接受的。多个学习器集成可以降低整体陷入局部极小的风险。

3、从表示的方面来看， 某些学习任务的真实假设可能不在当前算法的假设空间中，而多个学习器结合，可以扩大算法的假设空间，从而包含真实假设，有可能学到更好的近似。

4.2、结合策略

4.2.1、平均法

简单平均：     加权平均：其中wi为权重，要求

加权平均的权值都是在训练过程中学出来的，现实样本中通常不充分或者存在噪声，会导致学到的权重不是完全可靠，尤其对于大规模数据来说，学习的权重参数较多，很容易导致过拟合。因此加权平均不一定比简单平均效果更好。一般来说，个体学习器性能差别不大时采用简单平均法，个体学习器差距较大时采用加权平均法。

4.2.2、投票法

 投票法分为：绝对多数投票法、相对多数投票法和加权投票法。

绝对多数投票法是指当且仅当某标记得票过半才会给出预测结果，否则就会拒绝预测。相对多数投票法是指在投票结果中选出得票最多的标记作为预测结果，若得票最多的有多个，则随机选取一个。在必须有输出的学习任务中，由于必须给出输出，所以绝对多数投票法将会退化为相对多数投票法，两者统称多数投票法。加权投票法是指每个投票结果都带有学得的权重，最终计算时将权重计算在内。

对于每个个体学习器，其输出h(x)={0,1},预测为某类别输出1，否则输出0，则称此投票法为硬投票（hard voting ）。若其输出为预测为某个类别的概率，则称为软投票（soft voting）。

鸢尾花数据集voting实例：

#导入库
from sklearn import datasets  
from sklearn import model_selection  
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier  
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.model_selection import train_test_split

# 载入数据集
iris = datasets.load_iris()  
# 只要第0,1列的特征
x_data, y_data = iris.data[:, 0:2], iris.target  
x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target,test_size=0.4,random_state=1024) 
# 定义三个不同的分类器
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(x_train,y_train)
dtree = DecisionTreeClassifier() 
dtree.fit(x_train,y_train)
LR = LogisticRegression()  
LR.fit(x_train,y_train)
voting = VotingClassifier([('knn',knn),('dtree',dtree), ('lr',LR)],voting = 'soft')   
voting.fit(x_train,y_train)

print("准确率为：")
print('knn:',knn.score(x_test,y_test))
print('dtree:',dtree.score(x_test,y_test))
print('LR:',LR.score(x_test,y_test))
print('voting:',voting.score(x_test,y_test))

输出为：

4.2.3、学习法

当训练数据很多时，更为有效的结合策略时学习法。学习法是通过一个次级学习器来进行结合，stacking是学习法的代表。次级学习器的输入是初级学习器的输出，次级学习器的训练集也是由初级学习器训练所得。

鸢尾花数据集stacking实例：

from sklearn import datasets  
from sklearn import model_selection  
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier  
from sklearn.tree import DecisionTreeClassifier
from mlxtend.classifier import StackingClassifier # pip install mlxtend
from sklearn.model_selection import train_test_split


# 载入数据集
iris = datasets.load_iris()  
# 只要第0,1列的特征
x_data, y_data = iris.data[:, 0:2], iris.target  
x_train,x_test,y_train,y_test = train_test_split(iris.data, iris.target,test_size=0.4,random_state=1024) 
# 定义三个不同的分类器
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(x_train,y_train)
dtree = DecisionTreeClassifier() 
dtree.fit(x_train,y_train)
LR = LogisticRegression()  
LR.fit(x_train,y_train)
stacking = sclf = StackingClassifier(classifiers=[knn, dtree, LR],meta_classifier=dtree)   
stacking.fit(x_train,y_train)

print("准确率为：")
print('knn:',knn.score(x_test,y_test))
print('dtree:',dtree.score(x_test,y_test))
print('LR:',LR.score(x_test,y_test))
print('stacking:',stacking.score(x_test,y_test))

输出为：

 

 

 

参考文献：《机器学习》——周志华

                  《统计学习方法》——李航