Pytorch：图卷积神经网络-概述，半监督学习(标签传播LP算法)和PyTorch Geometric(PyG)安装

Pytorch: 图卷积神经网络-概述，半监督学习(标签传播算法)和PyTorch Geometric(PyG)安装

Copyright: Jingmin Wei, Pattern Recognition and Intelligent System, School of Artificial and Intelligence, Huazhong University of Science and Technology

Pytorch教程专栏链接

---

---

本教程不商用，仅供学习和参考交流使用，如需转载，请联系本人。

Reference

A Comprehensive Survey on Graph Neural Networks

SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

应用

图神经网络是用来处理图数据的神经网络。

• 对于图上的节点，可以是对节点的半监督或者有监督的节点分类和回归

• 对于图上的边，可以是有监督分类。

• 对整个图，可以使用无监督学习得到整张图的表示，进行图的分类。

图卷积神经网络是这部分的重点，主要是对图上的结点进行分类。

图卷积

图像的卷积运算可以认为是基于欧式空间的运算，结点之间的排布是有序且均匀的。而在很多节点构成的图上，进行的卷积运算可以认为是基于非欧氏空间的运算。因此图卷积实际上是模拟传统的图像卷积，但是不同的是，图卷积是基于结点之间的空间关系来定义的。

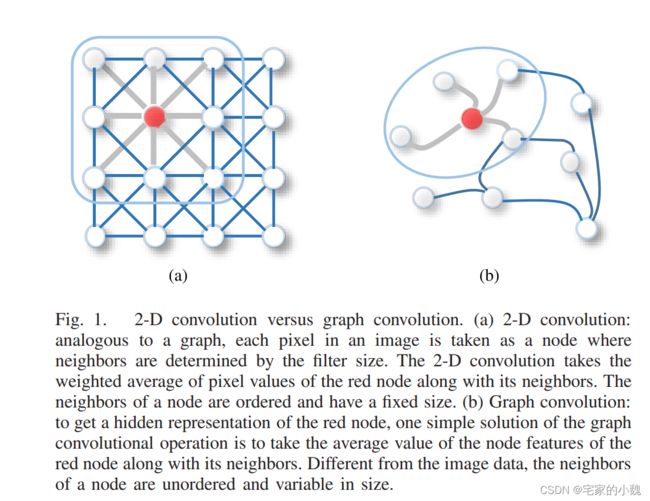
如图是第一篇论文中的图卷积介绍。将图像看做一种特殊的图，即可将图像的 2D 卷积和图卷积关联起来。

对于图像而言，每个像素代表图上的一个节点，每个像素所代表的结点和其附近的像素有一条边。通过一个 $3\times 3$ 的窗口(假设 kernel size = 3)，每个节点的邻域是周围的 $8$ 像素，再通过对每个通道上的中心结点及其相邻节点的像素值加权平均。

对于一般的图，同样基于空间的图卷积将中心节点表示成和相邻节点进行聚合，以获得该节点的新表示，只是这一表示不像图像的 2D 卷积那么均匀。

半监督学习

半监督学习是指训练数据中一些样本数据没有标签的情况。sklearn.semi_supervised 中的半监督估计器，能够利用这些附加的未标记数据来更好地捕获底层数据分布的形状，并将其更好地类推广到新的样本。当训练数据中有非常少量的有标签的点和大量的无标签的点时，这些算法可以表现良好。

标签传播(Label Propagation)

对于网络中的每一个节点，在初始阶段，Label Propagation 算法对每一个节点一个唯一的标签，在每一个迭代的过程中，每一个节点根据与其相连的节点所属的标签改变自己的标签，更改的原则是选择与其相连的节点中所属标签最多的社区标签为自己的社区标签，这便是标签传播的含义。随着社区标签的不断传播，最终紧密连接的节点将有共同的标签。

对于 Label Propagation 算法，假设对于节点 $x$ ，其邻居节点为 $x_1,x_2,\cdots ,x_k$ ，对于每一个节点，都有其对应的标签，标签代表的是该节点所属的社区。在算法迭代的过程中，节点 $x$ 根据其邻居节点更新其所属的社区。更新的规则是选择节点xx的邻居节点中，所属社区最多的节点对应的社区为其新的社区。

同步更新是指对于节点 $x$ ，在第 $t$ 代时，根据其所有邻居节点在第 $t-1$ 代时的社区标签对其标签进行更新。即：

$$C_x(t)=f(C_{x1}(t-1),C_{x2}(t-1),\cdots ,C_{xk}(t-1))$$

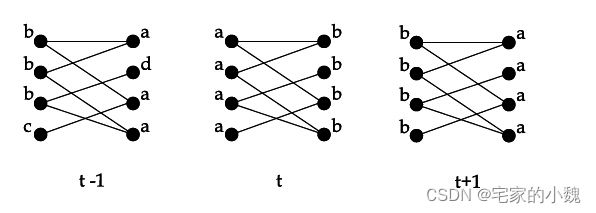
其中，$C_x(t)$ 表示的是节点 $x$ 在第 $t$ 代时的社区标签。函数 $f$ 表示的取的参数节点中所有社区个数最大的社区。同步更新的方法存在一个问题，即对于一个二分或者近似二分的网络来说，这样的结构会导致标签的震荡，如下图所示：

在上图中，两边的标签会在社区标签 $a$ 和社区标签 $b$ 不停地震荡。

对于异步更新方式，其更新公式为：

$$C_x(t)=f(C{x}_{i1}(t),\cdots ,C{x}_{im}(t),C{x}_{i(m+1)}(t-1),\cdots ,C{x}_{ik}(t-1))$$

其中，邻居节点 $x_{i1},\cdots ,x_{im}$ 的社区标签在第 $t$ 代已经更新过，则使用其最新的社区标签。而邻居节点 $x_{i(m+1)},\cdots ,x_{ik}$ 在第 $t$ 代时还没有更新，则对于这些邻居节点还是用其在第 $t-1$ 代时的社区标签。

对于节点的更新顺序可以顺序选择。

对于整个迭代过程，理想的情况下是图中节点的社区标签不再改变，此时迭代过程便可以停止。但是这样的定义方式存在一个问题，即对于某个节点，其邻居节点中存在两个或者多个最大的社区标签。对于这样的节点，其所属的社区是随机选取的，这样，按照上述的定义，此过程会一直执行下去。对上述的迭代终止条件重新修改：

迭代的终止条件是：对于每一个节点，在其所有的邻居节点所属的社区中，其所属的社区标签是最大的。

上述的定义可以表示为：如果用 $C_1,\cdots ,C_p$ 表示社区标签，$d_i^{C_j}$ 表示是节点 $i$ 的所有邻居节点中社区标签为 $C_j$ 的个数，则算法终止的条件为：对于每一个节点 $i$ ，有：

$$ifihaslabel{C}_{m}then{d}_i^{C_m}⩾d_i^{C_j}\forall j$$

这样的停止条件可以使得最终能够获得强壮的社区(Strong Community)，但是社区并不是唯一的。对于 Strong Community ，其要求对于每一个节点，在其社区内部的邻居节点严格大于社区外部的邻居节点，然而 Label Propagation 算法能够保证对于每一个节点，在其所属的社区内有足够多的邻居节点。

Label Propagation 算法的过程如下：

• 对网络中的每一节点初始化其所属社区标签，如对于节点 $x$ ，初始化其社区标签为 $C_x(0)=x$；

• 设置代数 $t$ ；

• 对于网络中的节点设置其遍历顺序和节点的集合 $X$ ；

• 对于每一个节点 $x\in X$ ，令 $C_x(t)=f(C{x}_{i1}(t),\cdots ,C{x}_{im}(t),C{x}_{i(m+1)}(t-1),\cdots ,C{x}_{ik}(t-1))$ ；

• 判断是否可以迭代结束，如果否，则设置 $t=t+1$ ，重新遍历。

Scikit-Learn 实现

标签传播表示半监督图推理算法的几个变体。

该模型的一些特性如下：

• 可用于分类和回归任务
• 使用内核方法将数据投影到备用维度空间

scikit-learn 提供了两种标签传播模型：LabelPropagation 和 LabelSpreading 。两者都通过在输入数据集中的所有项目上构建相似图来进行工作。

LabelPropagation 和 LabelSpreading 在对图形的相似性矩阵以及对标签分布的夹持效应(clamping effect) 方面的修改不太一样。 夹持效应允许算法在一定程度上改变真实标签化数据的权重。

LabelPropagation 算法执行输入标签的全加持(hard clamping)，这意味着 $\alpha =0$ 。夹持因子可以不一定很严格。例如 $\alpha =0.2$ 意味着我们将始终保留原始标签分配的 $80\%$ ，但该算法可以将其分布的置信度改变在 $20\%$ 以内。

LabelPropagation 使用原始相似性矩阵从未修改的数据来构建。 LabelSpreading 最小化具有正则化属性的损耗函数，因此它通常更适用于噪声数据。该算法在原始图形的修改版本上进行迭代，并通过计算 normalized graph Laplacian matrix(归一化图拉普拉斯矩阵)来对边缘的权重进行归一化。 这个过程也被用于 Spectral clustering。

class sklearn.semi_supervised.LabelPropagation(kernel='rbf', *, gamma=20, n_neighbors=7, max_iter=1000, tol=0.001, n_jobs=None)[source]

标签传播模型有两种内置的核函数。核的选择会影响算法的可扩展性和性能。 以下是可用的核：

rbf $(\exp (-\gamma |x-y{|}^2),\gamma >0)—\gamma$ 通过关键字 $\gamma$ 来指定。

knn $(1[x^{\prime }\in kNN(x)])—k$ 通过关键字 n_neighbors 来指定。

RBF 核将产生一个全连接的图形，它通过密集矩阵在内存中表示。这个矩阵可能非常大，加之算法每次迭代执行全矩阵乘法的计算成本，我们可能会有特别长的运行时间。另一方面，KNN 核能够产生更多的内存友好的稀疏矩阵，这可以大幅度的减少运行时间。

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.semi_supervised import LabelPropagation, LabelSpreading

iris = datasets.load_iris() # 导入数据集

# 设置30%标签失效
rng = np.random.RandomState(0)
random_unlabeled_points = rng.rand(len(iris.target)) < 0.3 
labels = np.copy(iris.target)
labels[random_unlabeled_points] = -1

X = iris.data[:, 0: 2]  # 取数据集前两列特征向量，方便可视化
y = labels
h = .02  # 网格中的步长

lp_clf = LabelPropagation(max_iter=200) # 使用标签传播算法分类
# lp_clf.fit(iris.data, labels)
lp_clf.fit(X, y)
lp_clf.score(X, y) # 精度

0.6266666666666667

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

plt.figure(figsize=(12, 8))
 
Z = lp_clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)

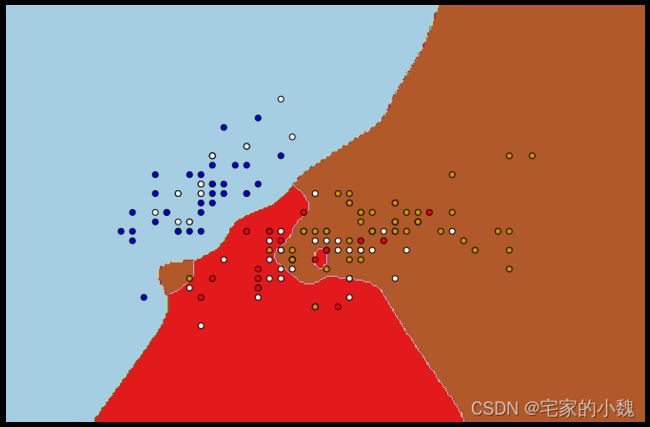
plt.contourf(xx, yy, Z, cmap = plt.cm.Paired)
plt.axis('off')

color_map = {-1: (1, 1, 1), 0: (0, 0, .9), 1: (1, 0, 0), 2: (.8, .6, 0)}
colors = [color_map[Y] for Y in y]
plt.scatter(X[:, 0], X[:, 1], c = colors, edgecolors = 'black')
plt.show()

​

​

基于图卷积网络的半监督学习

在引用的第二篇文章中，Thomas N. Kipf 提出的图卷积深度学习网络，能用于图上节点分类的半监督学习。其中前向传播的规则为：

$$H^{(l+1)}=\sigma \left({\tilde{D}}^{(-\frac{1}{2})}\tilde{A}{\tilde{D}}^{(-\frac{1}{2})}{H}^{(l)}{W}^{(l)}\right)$$

$\tilde{A}=A+I_N$ 是无向网络图的邻接矩阵加上一个单位矩阵；$\tilde{D}={\sum }_j{A}_{ij}$ ；$W^{(l)}$ 是可训练的权重参数；$\sigma (\cdot )$ 表示激活函数。

针对两层的半监督的节点分类的网络模型可以简单概括为：

$$Z=f(X,A)=softmax(\hat{A}ReLU(\hat{A}X{W}^{(0)})W^{(1)})$$

$\hat{A}={\tilde{D}}^{(-\frac{1}{2})}\tilde{A}{\tilde{D}}^{(-\frac{1}{2})}$ ；$X$ 表示节点的特征矩阵；$ReLU$ 为线性修正单元激活函数。

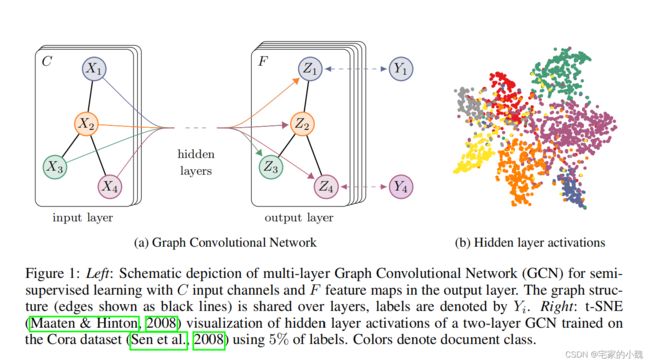
图为论文中 GNN 的网络结构。在图中，输入包含 $C$ 个通道，输出有 $F$ 个特征映射。在输入层中，$X_i$ 表示节点的特征，黑色的连线表示节点之间的连接方式，$Y_i$ 表示节点的类别标签。

PyTorch Geometric 库

PyTorch Geometric(PyG) 是在 PyTorch 上的图深度学习拓展库，它包括各种论文中的对图和其他不规则结构进行深度学习的方法，即图深度学习。它包括一些简单易用的数据处理程序，支持 GPU 计算，包含大量公共基准数据集，方便用来使用和测试模型。

PyG 主要包括深度学习的层模块 torch_geometric.nn，数据预处理模块 torch_geometric.data，常用数据集模块 torch_geometric.datasets，数据操作模块 torch_geoetric.transform 即 torch_geometric.utils 模块和 torch_geometric.io 模块。

模块	类 / 函数	功能
torch_geometric.nn	MessagePassing()	建立消息传递层的类
	GCNconv()	论文 Semi-Supervised Classification with Graph Convolutional Networks 使用的图卷积层
	ChebConv()	论文 Convolutional Neural Networks on Graphs with Fast Localized SPectral Filtering 使用的 Chebyshev 谱图卷积层
	SAGEConv()	论文 Inductive Representation Learning on Large Graphs 使用的 GraphSAGE 算子层
	GATConv()	论文 Graph Attention Networks 使用的图注意力算子层
	BatchNorm()	对一个 batch 的结点做批处理 normalization 操作
	InstanceNorm()	对一个 batch 的节点特征做实例 normalizaiton 操作
torch_geometric.data	Data()	网络图的数据类
	Dataset()	用于创建网络数据集的类
	DataLoader()	数据加载器
torch_geometric.datasets	KarateClub()	空手道俱乐部网络数据集
	Planetoid()	文献引用的网络数据集，包含 Cora, CiteSeer, PubMed 三个应用网络数据
torch_geometric.transforms	Compose()	组合多种数据增强操作
	Constant()	为每个节点特征加上一个常数
	Distance()	将节点的欧几里得距离保存在其边属性中
	OneHotDegree()	将节点度使用 one-hot 编码添加到节点特征中
	KNNGraph()	基于节点位置创建一个 KNN 图
torch_geometric.utils	degree()	计算指定节点的度
	is_undirected()	判断是否为无向图
	to_undirected()	转化为无向图
	to_networkx()	将数据转化为 networkx 可使用的 networkx.DiGraph 数据形式

该库的更多使用方法可以参考该网站：https://pytorch-geometric.readthedocs.io/en/latest/ 。

安装 PyG

我的 conda 直接安装会出现 inconsistent 的问题，所以我选择 pip3 挨个安装依赖包再安装 PyG 。其他安装方法参考 https://pytorch-geometric.readthedocs.io/en/latest/notes/installation.html# 。

首先确认你的 Python, Pytorch, Cuda 三者版本。

import torch

print(torch.__version__)
print(torch.version.cuda)

1.8.1
10.1

from sys import version_info

version_info # 显示就是python版本：3.8.5

sys.version_info(major=3, minor=8, micro=5, releaselevel='final', serial=0)

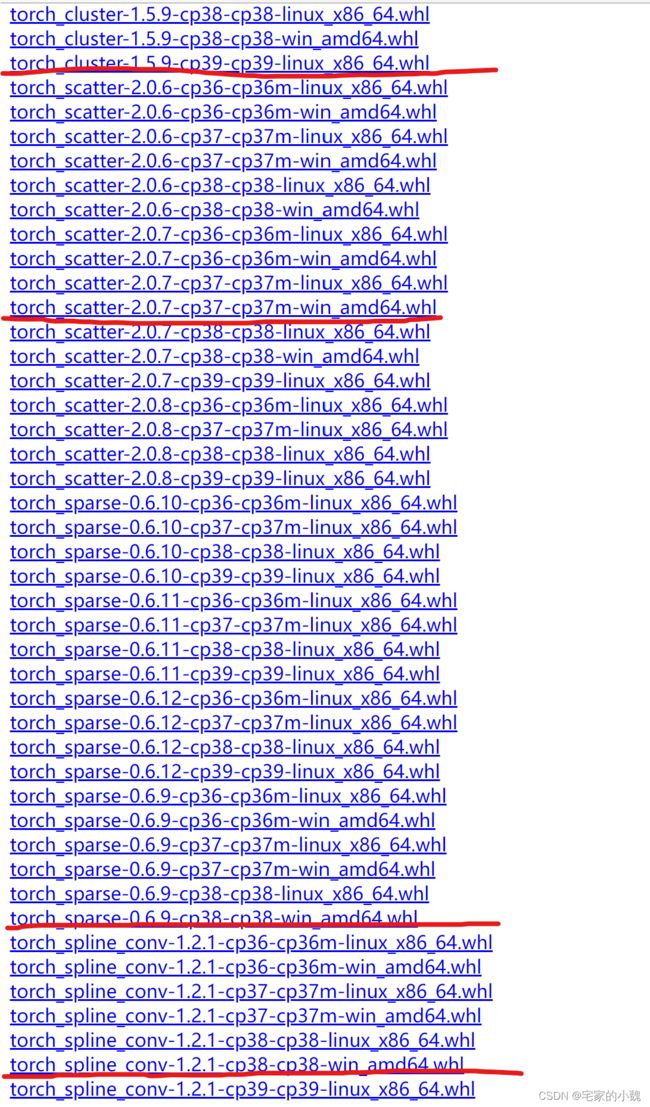
打开 https://pytorch-geometric.com/whl/ 。选择对应的 torch 版本和 cuda 版本。比如我的是 pytorch 1.8.1 + cuda 10.1 ，则我选择 torch-1.8.1 + cu101 。

下载 torch_gemetric 的 backup pkg 的 whl 驱动，即 torch_cluster, torch_scatter, torch_sparse, torch_spline_conv。版本选择，cp3xm 是 python 版本的意思，比如说我是 python 3.8 ，则我选择的包都带 cp38 。win / linux 是对应的操作系统，amd64 对应 64 位电脑。

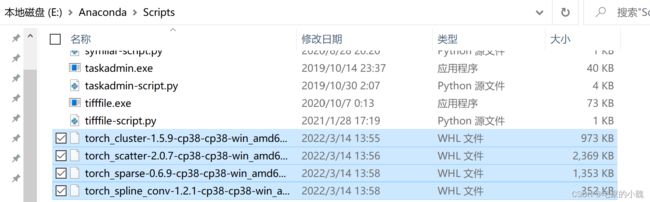
我选的是以上四个版本，请大家根据自己电脑而来。

将这四个驱动文件复制进 ./Anaconda3/Scripts 。

打开 Anaconda 的终端，进入你要安装的 conda 环境。在安装 torch-geometric 前，需要把这四个包安装好。

torch-geometric 安装前还需要安装其他一些常用包，比如 numpy, pandas, scikit-learn, requests 等。这些都是常用包，这里默认大家已经都装好了

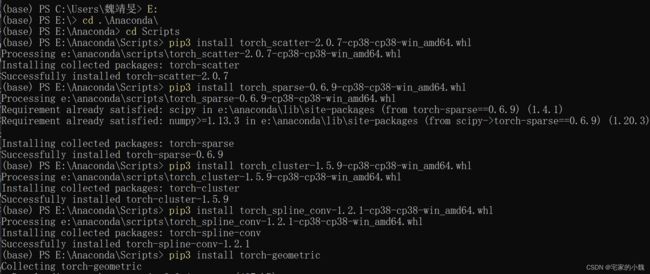
cd .\Anaconda\Scrpits
pip3 install torch_scatter-2.0.7-cp38-cp38-win_amd64.whl
pip3 install torch_sparse-0.6.9-cp38-cp38-win_amd64.whl
pip3 install torch_cluster-1.5.9-cp38-cp38-win_amd64.whl
pip3 install torch_spline_conv-1.2.1-cp38-cp38-win_amd64.whl
pip3 install torch-geometric # 安装torch-gnn库

之后可以测试是否安装成功

import torch_geometric.nn as gnn
import torch_geometric
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import to_networkx
import networkx as nx

torch_geometric.__version__

'2.0.4'