算法(一):智能小车速度控制(PID模糊控制)
概览
- 一、前言
- 二、基于PID 的速度控制
-
- 1.PID控制器
- 2.PID速度控制
- 二、基于模糊控制的速度控制
-
- 1.变量的模糊化
- 2.模糊查询表的计算
- 3.模糊查询表设置车速
- 三、总结
一、前言
本科的时候参加飞思卡尔比赛,在队友的神助攻下有幸拿了国奖,比赛中使用了模糊控制算法。这段时间正好看到了模糊控制算法,就把以前的代码翻出来,顺便总结一下PID和模糊控制算法,希望自己能养成记录知识点的好习惯。
二、基于PID 的速度控制
在控制领域,PID算法是应用最广泛的算法之一。小到电机的转速,大到机器人稳定性的控制。在实现智能小车速度的闭环控制时首选简单有效的PID控制算法。
1.PID控制器
PID(Proportion Integration Differentiation)控制器包括P比例、I积分和D微分三个控制单元,协同工作保证控制系统快速到达并稳定于目标值。PID控制算法的公式:
u ( t ) = K p e r r ( t ) + K i ∫ e r r ( t ) d t + K d d e r r ( t ) d t u(t)=K_perr(t)+K_i\int err(t)dt +K_d\frac{derr(t)}{dt} u(t)=Kperr(t)+Ki∫err(t)dt+Kddtderr(t)
对其进行离散化:
u ( n ) = K p e r r ( n ) + K i ∑ k = 0 n e r r ( k ) + K d ( e r r ( n ) − e r r ( n − 1 ) ) u(n)=K_perr(n)+K_i\sum_{k=0}^n err(k) +K_d(err(n)-err(n-1)) u(n)=Kperr(n)+Kik=0∑nerr(k)+Kd(err(n)−err(n−1))
1) K p K_p Kp比例控制
控制器的反应速度与 K p K_p Kp有关,该系数越大,控制系统反应更灵敏。但是 K p K_p Kp过大会引起较大的超调,并产生震荡,破坏系统的稳定性。因此在调整 K p K_p Kp参数时应从低到高增加,选择系统达到响应快并稳定的效果时的参数。
2) K i K_i Ki积分控制
只要控制系统存在误差,该系数对系统的作用就会不断增强。只有误差err消失即系统稳定在目标值时,控制作用才不会变化。由此可见积分控制的调节会消除系统的静态误差。
3) K d K_d Kd微分控制
为了抑制系统的超调和振荡,在控制系统中增加微分控制。通过对控制系统未来的预估,及时对控制量进行调整,提升系统的稳定性。
2.PID速度控制
刚开始对小车的速度控制采用位置式PID控制算法,即常用的PID控制算法。但是位置式PID算法使用过去误差的累加值,容易产生较大的累计误差。而且由于小车的目标速度时刻在变化,err值需要不断的累加,可能出现err_sum溢出的情况。因此对位置式加以变换,得到增量式PID控制算法:
△ u = u ( n ) − u ( n − 1 ) = K p ( e r r ( n ) − e r r ( n − 1 ) ) + K i e r r ( n ) + K d ( e r r ( n ) − 2 e r r ( n − 1 ) + e r r ( n − 2 ) ) \triangle u=u(n)-u(n-1)=K_p(err(n)-err(n-1))+K_ierr(n) +K_d(err(n)-2err(n-1)+err(n-2)) △u=u(n)−u(n−1)=Kp(err(n)−err(n−1))+Kierr(n)+Kd(err(n)−2err(n−1)+err(n−2))
由此计算出:
u ( n ) = u ( n − 1 ) + K p ( e r r ( n ) − e r r ( n − 1 ) ) + K i e r r ( n ) + K d ( e r r ( n ) − 2 e r r ( n − 1 ) + e r r ( n − 2 ) ) u(n) = u(n-1) + K_p(err(n)-err(n-1))+K_ierr(n) +K_d(err(n)-2err(n-1)+err(n-2)) u(n)=u(n−1)+Kp(err(n)−err(n−1))+Kierr(n)+Kd(err(n)−2err(n−1)+err(n−2))
int speed_control(void)
{
int i;
speed_set=get_speed_set();//设置车速
//设置PID参数
kp_motor=33;
ki_motor=0.038;
kd_motor=0.04;
for(i=0;i<9;i++)
error[i]=error[i+1];
error[9]=speed_set-speed;
de=kp_motor*(error[9]-error[8])+ki_motor*error[9]-kd_motor*(speed_save[9]-2*speed_save[8]+speed_save[7]);
pwm1 = pwm1_old+de;
speed_set_old=speed_set;
pwm1_old=pwm1;
return pwm1;//输出PWM波
}
二、基于模糊控制的速度控制
拥有响应迅速地速度控制系统对于提升小车的速度是不够的,还需要根据赛道情况设置不同的车速以实现小车最快地通过不同的路况。这时,可以考虑模糊控制的思想根据路况及小车当前的状态对目标车速进行设置。
1.变量的模糊化
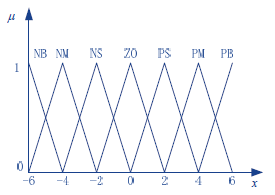
在模糊控制中,输入输出变量大小用语言形式进行描述。常选用的7个语言值为{负大,负中,负小,零,正小,正中,正大},即{NB,NM,NS,O,PS,PM,PB}。
对小车当前行驶方向和赛道方向形成的偏差e及其变化率ec作为模糊控制器的输入,小车的目标车速为模糊控制器的输出。设偏差值的模糊量为E,偏差变化率模糊量为EC,U为目标车速。为了让速度切换更加细腻流畅,设置偏差e、偏差变化ec和控制量u的基本论域为[-6,6],并划分为13个等级,即{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}。
E、EC和U均使用三角形隶属函数进行模糊化
/**
* 列坐标:NB,NM,NS,O,PS,PM,PB
* 横坐标:-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6
* @param 建立输入、输出隶属度函数,进行微调调整模糊量的范围
*/
/***************************************误差隶属度函数***************************************/
float Input1_Terms_Membership[7][13] =
{ 1,0.15,0,0,0,0,0,0,0,0,0,0,0,
0,0.2,1,0.2,0,0,0,0,0,0,0,0,0,
0,0,0,0.2,1,0.2,0,0,0,0,0,0,0,
0,0,0,0,0,0.1,1,0.1,0,0,0,0,0,
0,0,0,0,0,0,0,0.1,1,0.1,0,0,0,
0,0,0,0,0,0,0,0,0,0.2,1,0.2,0,
0,0,0,0,0,0,0,0,0,0,0,0.2,1
};
/***************************************误差变化率隶属度函数***************************************/
float Input2_Terms_Membership[7][13] =
{ 1,0.15,0,0,0,0,0,0,0,0,0,0,0,
0,0.2,1,0.2,0,0,0,0,0,0,0,0,0,
0,0,0,0.2,1,0.2,0,0,0,0,0,0,0,
0,0,0,0,0,0.1,1,0.1,0,0,0,0,0,
0,0,0,0,0,0,0,0.1,1,0.1,0,0,0,
0,0,0,0,0,0,0,0,0,0.2,1,0.2,0,
0,0,0,0,0,0,0,0,0,0,0,0.2,1
};
/***************************************输出(速度)***************************************/
float Output_Terms_Membership[7][13] =
{ 1,0.15,0,0,0,0,0,0,0,0,0,0,0,
0,0.2,1,0.2,0,0,0,0,0,0,0,0,0,
0,0,0,0.2,1,0.2,0,0,0,0,0,0,0,
0,0,0,0,0,0.1,1,0.1,0,0,0,0,0,
0,0,0,0,0,0,0,0.1,1,0.1,0,0,0,
0,0,0,0,0,0,0,0,0,0.2,1,0.2,0,
0,0,0,0,0,0,0,0,0,0,0,0.2,1
};
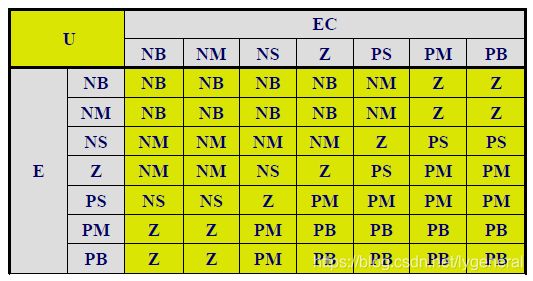
2.模糊查询表的计算
/**
* 纵轴为E(error),横轴为EC(error_delta),值为速度七档NB(0),NM(1),NS(2),Z(3),PS(4),PM(5),PB(6)速度由小变大再变小
* 列坐标:E(NB,NM,NS,O,PS,PM,PB)
* 横坐标:EC(NB,NM,NS,O,PS,PM,PB)
* 值:U(1:NB:2,NM,3:NS,4:O,5:PS,6:PM,7:PB)
* @param 模糊控制规则表,调整速度变化趋势
*/
int Rule[7][7] =
{ 1,1,2,2,6,7,7,
1,1,2,2,6,6,6,
1,2,3,4,5,6,6,
1,3,4,4,4,5,7,
2,2,3,4,5,6,7,
2,2,2,2,6,7,7,
1,1,2,2,6,7,7
};//调试参数
规则库蕴含的模糊关系:
R = ( E × E C ) × C R=(E\times EC)\times C R=(E×EC)×C
其中,模糊运算 × \times ×表示“取小”。
计算出模糊规则蕴含的模糊关系R后,通过遍历E和EC所有的论域对模糊值进行选取并计算模糊输出值:
U ∗ = ( E ∗ × E C ∗ ) ∘ R U^*=(E^* \times EC^*)\circ R U∗=(E∗×EC∗)∘R
其中, ∘ \circ ∘表示模糊矩阵的合成,类似于普通矩阵的乘积运算,将乘积运算换成“取小”,将加法运算换成“取大”。
在遍历过程中,对E和EC所有论域对应的模糊输出值一一采取加权平均法去模糊化,得到最终的模糊控制器查询表。
float R[169][13] = { 0 };
float R1[13][13] = { 0 };
float AdBd1[13][13] = { 0 };
float R2[169] = { 0 };
float AdBd2[169] = { 0 };
float R3[169][13] = { 0 };
float Cd[13] = { 0 };
float Fuzzy_Table[13][13] = { 0 };
float SPEED[13] = { 200,220,230,240,250,270,300,270,250,240,230,220,200 };//调试参数
int Max_Input1_value = 0, Max_Input2_value = 0;
/**
* @param 模糊化过程实现论域内不同值对应隶属度最大的语言值
*/
int E_MAX(int e)
{
int i = 0, max = 0;
for (i = 0; i < 7; i++)
if (Input1_Terms_Membership[i][e] > Input1_Terms_Membership[max][e])
max = i;
return max;
}
int EC_MAX(int ex)
{
int i = 0, max = 0;
for (i = 0; i < 7; i++)
if (Input2_Terms_Membership[i][ex] > Input1_Terms_Membership[max][ex])
max = i;
return max;
}
void calculate()
{
/***************************************计算所有规则模糊关系的并集Rule***************************************/
int i = 0, j = 0, k = 0;
int Input1_value_index = 0, Input2_value_index = 0;
//计算Rule(初始化),计算Rij,并对所有的R取并集,R=(EXEC)XU
for (Input1_Terms_Index = 0; Input1_Terms_Index < 7; Input1_Terms_Index++)
for (Input2_Terms_Index = 0; Input2_Terms_Index < 7; Input2_Terms_Index++)
{
// E和EC的语言值两两组合及其输出计算Rule
Output_Terms_Index = Rule[Input1_Terms_Index][Input2_Terms_Index] - 1;
k = 0;
for (i = 0; i < 13; i++)
for (j = 0; j < 13; j++)
{
// E和EC进行取小运算
if (Input1_Terms_Membership[Input1_Terms_Index][i] < Input2_Terms_Membership[Input2_Terms_Index][j])
R1[i][j] = Input1_Terms_Membership[Input1_Terms_Index][i];
else
R1[i][j] = Input2_Terms_Membership[Input2_Terms_Index][j];
// 转换R1矩阵为R2一维向量
R2[k] = R1[i][j];
k++;
}
/// R[i][j])
R[i][j] = R3[i][j];
}
}
/*************************对于每种可能的E、EC的精确取值模糊化后进行推理得到模糊输出Cd,Cd=(AdxBd)oR*************************/
for (Input1_value_index = 0; Input1_value_index < 13; Input1_value_index++) {
for (Input2_value_index = 0; Input2_value_index < 13; Input2_value_index++)
{
for (j = 0; j < 13; j++)
Cd[j] = 0;
int kd = 0;
float temp = 0;
Max_Input1_value = E_MAX(Input1_value_index); ///<找出误差隶属度最大的语言值
Max_Input2_value = EC_MAX(Input2_value_index); ///<找出误差变化率隶属度最大的语言值
for (i = 0; i < 13; i++)
for (j = 0; j < 13; j++)
{
// E(Ad)和EC(Bd)进行取小运算
if (Input1_Terms_Membership[Max_Input1_value][i] < Input2_Terms_Membership[Max_Input2_value][j])
AdBd1[i][j] = Input1_Terms_Membership[Max_Input1_value][i];
else
AdBd1[i][j] = Input2_Terms_Membership[Max_Input2_value][j];
AdBd2[kd] = AdBd1[i][j];
kd++;
}
for (i = 0; i < 169; i++)
for (j = 0; j < 13; j++)
{
// 模糊矩阵的合成,将乘积运算换成“取小”,将加法运算换成“取大”
if (AdBd2[i] < R[i][j])
temp = AdBd2[i];
else
temp = R[i][j];
if (temp > Cd[j])
Cd[j] = temp;
}
/*************************去模糊化(加权平均法),计算实际输出*************************/
float sum1 = 0, sum2 = 0;
float OUT;
for (i = 0; i < 13; i++)
{
sum1 = sum1 + Cd[i];
sum2 = sum2 + Cd[i] * SPEED[i];
}
OUT = (int)(sum2 / sum1 + 0.5);///<四舍五入
Fuzzy_Table[Input1_value_index][Input2_value_index] = OUT;
cout << OUT << ",";
}
cout << endl;
}
}
3.模糊查询表设置车速
将模糊查询表复制进入代码程序,将实际的e和ec映射到论域中后,在模糊查询表中查询结果并设置目标车速。
int_16 Fuzzy_Table[13][13]=
{
203,211,211,211,226,226,230,230,228,210,210,210,210,
209,221,221,221,238,238,241,241,237,231,231,231,227,
209,221,221,221,238,238,241,241,237,231,231,231,227,
209,221,221,221,238,238,241,241,237,231,231,231,227,
215,238,238,238,245,245,266,266,246,237,237,237,232,
215,238,238,238,245,245,266,266,246,237,237,237,232,
218,250,250,250,276,276,283,283,280,245,245,245,216,
218,250,250,250,276,276,283,283,280,245,245,245,216,
232,240,240,240,250,250,271,271,246,236,236,236,217,
226,230,230,230,236,236,239,239,236,214,214,214,208,
226,230,230,230,236,236,239,239,236,214,214,214,208,
226,230,230,230,236,236,239,239,236,214,214,214,208,
211,211,211,211,226,226,230,230,228,208,208,208,203
} ;
int_16 get_speed_set(void) {
int_16 E = 0, EC = 0;
int_16 speed_target;
static int_16 re_pos = 0, ek = 0, eck = 0;
float ke = 400, kec = 10;
ek = 2500 - row;
eck = 2500 - row - re_pos;
re_pos = ek;
if (ek > 0) {
E = (int_32)(ek / ke + 0.5);
}
else {
E = (int_32)(ek / ke - 0.5);
}
//将E的论域转换到模糊控制器的论域
if (E > 6)
E = 6;
else if (E < -6)
E = -6;
if (eck > 0) {
EC = (int_16)(eck / kec + 0.5);
}
else {
EC = (int_16)(eck / kec - 0.5);
}//将EC的论域转换到模糊控制器的论域
if (EC > 6)
EC = 6;
else if (EC < -6)
EC = -6;
speed_target = (int_16)(Fuzzy_Table[E + 6][EC + 6]);
return speed_target ;
}
三、总结
本文首先对PID控制器进行了简单的阐述,并应用于车速控制中。然后引入模糊控制对目标车速进行设置,实现速度的平稳过渡。PID算法和模糊控制算法在保证行驶平稳性的前提下,最大幅度地提升小车的行驶速度。源代码见Github:FuzzySpeed,如有问题可私聊。
参考资料
[1]详细讲解PID控制
[2]PID控制算法原理(抛弃公式,从本质上真正理解PID控制)
[3]初识PID-搞懂PID概念
[4]模糊控制——基本原理
[5]基于单目视觉的智能车速度模糊控制系统
[6]模糊算法在智能车控制中的应用