COMSOL案例学习（4）：水杯中的自然对流
✅作者简介：大家好我是Xlong，一枚正在学习COMSOL、Python的工科研究僧
个人主页: Xlong的个人博客主页
系列专栏：COMSOL学习
如果觉得博主的文章还不错的话，请支持一下博主哦
案例链接：
http://cn.comsol.com/model/free-convection-in-a-water-glass-195
http://cn.comsol.com/model/free-convection-in-a-water-glass-195
一、重要图表（仿真运行30min）
1.流经玻璃杯顶面 （实线）、侧壁 （点虚线）和底面 （虚线）的热通量
图1 流经玻璃杯顶面 （实线）、侧壁 （点虚线）和底面 （虚线）的热通量
从图1可以看出绝大部分热量通过下底面传入玻璃杯中的水，这是因为玻璃杯与周围环境的换热系数小。
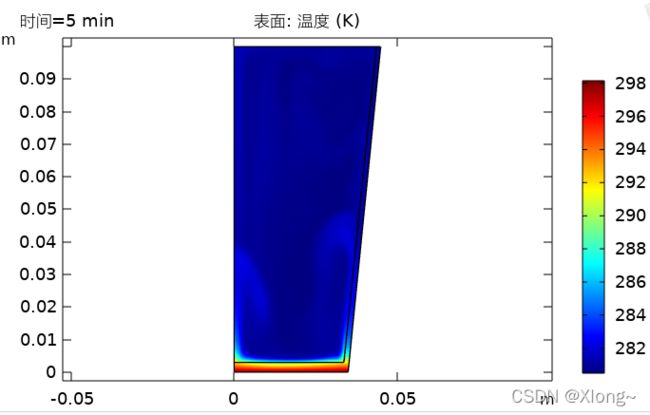
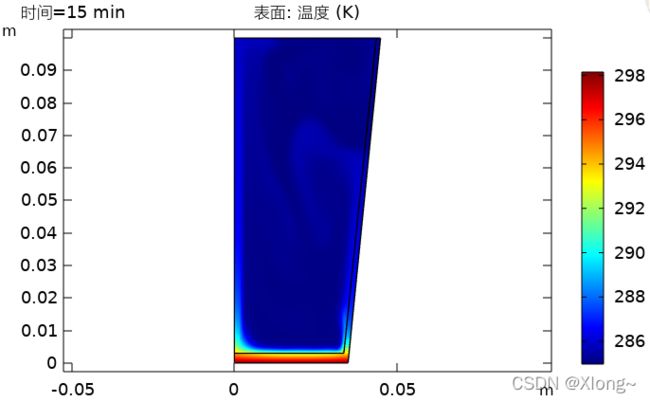
2.等间隔时间的温度分布(range(0,5min,30min))
3.速度场的流线可视化效果
二、建模操作
1.选二维轴对称、非等温流动中的层流、一般研究中的瞬态。
2.首先进行全局定义、全局定义里的参数在后面都可以任意调用。
3.创建选择功能：比如选择了域2，单击创建选择，在选择名称文本框中重命名为“水”，这样在下一次就可以直接选择“水”，而不需要选域2。这一功能在有多个相同的域需要被重复添加的情况下运用十分方便。
4.由于存在大量二次流，因此需要减小容差。
5.单击显示默认求解器→展开解1节点→单击瞬态求解器→点击以展开绝对容差栏→从容差方法列表中选择手动→绝对容差文本框中键入“2.5e-5”
三、总结归纳
1.玻璃杯中水的自然对流，是化工设备中经常被忽略的一种现象。但是，在发酵过程、铸造以及生化反应器等特定情况下，这种现象相当重要。自然对流还可能是小型反应器中的主要传输方式。
2.本案例中的玻璃杯由于旋转对称，所以可以采用二维轴对称几何来对整个系统进行建模。这样可以大大节省计算资源，同时也不会影响计算结果。如下图所示。
图
3.初始条件：玻璃杯和水温都是5℃，周围空气和桌子保持恒温25℃，玻璃杯壁厚度有限，具有特定热导率。
4.边界条件：假设桌子表面与杯底是理想接触（热阻为0），则杯底温度也是25℃。在顶面和侧壁表面，使用对流热通量边界条件，热量传递由玻璃杯与周围环境间的温差驱动：
其中，
是热通量，
是对流换热系数。
5.对于流场：在内部边界（玻璃杯与玻璃杯附近的水之间）采用无滑移条件，在旋转轴上应用轴对称条件，在开放表面应用滑移条件。
①无滑移边界条件：流体在壁面处的速度（或相对速度）为零
②滑移边界条件：流体在壁面处的速度（或相对速度）不为零
6.此示例中的仿真运行了2min，博主试了一下30min,运算结果见一、重要图表。
7.将流量设为不可压缩来确保质量守恒，然后锁定封闭腔体中的压力以获得模型。使用布辛涅斯克近似来包含浮力。
布辛涅斯克近似（Boussinesq approximation） ： 描述流体运动最基本的方程即纳维-斯托克斯方程（简称N-S方程），然而其复杂性和非线性，只能通过数值方法求解，同时还需要针对不同流体的情况，对N-S方程做一定的简化，这样才能既保证结果的准确性，又保证效率。最常用的假设就是布辛涅司克近似（Boussinesq approximation）。
在自然对流中,除了动量方程中的浮力项中的密度温度的函数外,其他所有求解方程中的密度Boussinesq 假设均认为为常数,这一近似称为布辛涅司克近似。
布辛涅司克近似适用于密度变化不大的流体运动，而对于自然界中绝大多数流体，这种假设是适用的。
8.
矢量是什么？
9.流体离散化：
10. 压力点约束：
流体模型中，所说的压力一般指压力差而非绝对压力，为了提高流体模型计算的收敛性，需要引入一个压力参考点来提高收敛性，这个参考点的位置可以是任意的。所以在很多仿真案例中，可以看到设定一个入口速度，一个出口压力为零。事实上，如果外界压力为一个大气压，流道内的真实压力值就得在计算结果上加上一个大气压。如果没有定义压力边界，这意味着全域中没有合适的能够作为压力降计算的基准点。从某种意义上来讲，这种计算应该是有无穷多解的，因为你可以得到很多组合适的相对压力降满足条件的结果。这样一来，求解器会很不容易得到收敛解。所以在这种情况下，有时候我们就添加一个压力约束点，把它作为一个基准点来进行仿真，得到一个特解。
11.对于层流，当瑞利数小于
时，热传导的热量远多于对流。
12、二次流：
流体力学中，二次流的概念如下定义：假如沿一边界的流动因受到横向压力的作用，产生了平行于边界的偏移，则靠近边界的流体层由于速度较小，就比离边界较远的流体层偏移得厉害，这就导致了叠加于主流之上的二次流。
13.结果工具栏的更多派生值，里面有用于计算结果再处理的一些功能，比如平均值、积分、最大值、最小值。
持续更新中......
原创不易，各位看官请随手点下Follow和Star，感谢！！！