SAS 数值存储方式和精度问题

本文链接：https://www.cnblogs.com/snoopy1866/p/16021137.html

1 数值存储方式

SAS使用8个字节存储数值，使用浮点计数法表示数值。
浮点计数法由4个部分组成：符号位（Sign）、基数（Base）、指数（Exponent）、尾数（Mantissa），这4个部分分别提供以下作用：

• 符号位：代表该数值是正数还是负数
• 基数：SAS系统中的基数默认为2。
• 指数：代表基数被乘的倍数
• 尾数：定义数值范围的一个小数

将计算机内部存储的数值转化为10进制数值的公式为：\(\color{red}{Sign}\)*(\(\color{purple}{Mantissa}\) * Base^{$\color{green}{Exponent}$})
下图展示了SAS用8个字节表示浮点数的具体情况：

即第1位为符号位，第2-12位为指数位，13-64位为尾数位，符号位中，0表示正数，1表示负数。
例如：Sign = 1, Exponent = 3, Mantissa = 1492，在10进制下代表：(-1) * (0.1492 * 10³) = -149.2，在2进制下表示：(-1) * (0.1492 * 2²) = -1.1936;

2 产生的问题

不是所有浮点数都能用8个字节精确地表示，某些浮点数甚至无法用有限个字节精确地表示，这在任何进制下都是存在的问题。
例如：10进制下的0.1在16进制下表示为3FB999999999999999999999999999999...，2/3在10进制下表示为0.666666666666666666666...
当计算机面对这种情况时，有两种选择：
（1）Truncation：2/3+2/3+2/3 = 0.666666 + 0.666666 + 0.666666 = 1.999998
（2）Rounding: 2/3+2/3+2/3 = 0.666667 + 0.666667 + 0.666667 = 2.000001
但这两种选择都无法完美解决精度问题，而且随着运算次数的累计，精度问题会愈发凸显。

来看下面一个例子：

/*DO 迭代生成0.1~0.9*/
data s1;
    do a = 0.1 to 0.9 by 0.1;
        index + 1;
        output;
    end;
run;

/*手动输入0.1~0.9*/
data s2;
    do b = 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9;
        index + 1;
        output;
    end;
run;

/*合并s1-s2*/
data s3;
    merge s1 s2;
    by index;
    if a = b then A_eq_B = "Y";
run;

proc print data = s3;
    var index a b A_eq_B;
run;

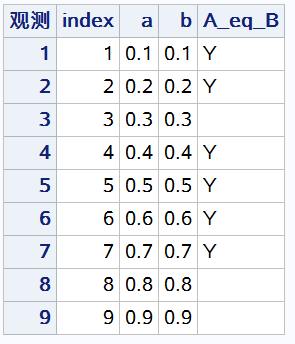
可以看到PROC PRINT打印出来的结果中显示，A，B两列显示完全一致，但其中0.3,0.8和0.9却出现了A≠B的情况。
为了能够看到SAS内部储存的实际数值，使用十六进制输出格式输出结果：

proc print data = s3;
    var index a b A_eq_B;
    format a hex16. b hex16.;
run;

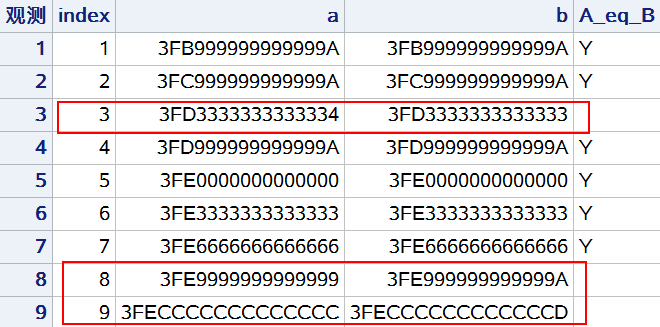
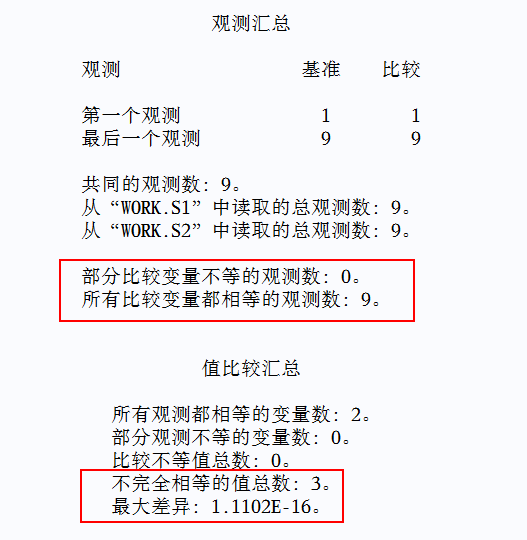
由此可见，是DO循环迭代计算导致的误差累计，最终导致A和B两列实际存储的数值存在微小差异。
这种精度损失可能会在下述场景中导致问题：

• 使用 IF，SELECT，WHERE语句比较两个不同计算方法得出的数值，或与显式指定的数值比较时；
• 对数据集取子集时；
• 使用 PROC COMPARE 过程比较两个数据集时
• 对基于计算产生的浮点数进行分类分析时
• PROC REPORT或其他过程步的输出可能会显示出奇怪的小数（例如：-0.00）

3 解决办法

以下3种方式可以解决SAS中存在的大多数精度问题：

• 使用 ROUND 函数
• 为数值变量创建字符串版本的变量
• 利用过程步中的选项

（1）ROUND函数
在不需要特别精确的情况下，可以使用ROUND函数仅比较前几位小数。

data s3;
    merge s1 s2;
    by index;
    a_r = round(a, 0.1);
    b_r = round(b, 0.1);
    if a_r = b_r then A_eq_B = "Y";
run;
proc print data = s3;
    var index a b A_eq_B a_r b_r;
    format a hex16. b hex16. a_r hex16. b_r hex16.;
run;

（2）创建数值变量的字符串版本

data s3;
    merge s1 s2;
    by index;
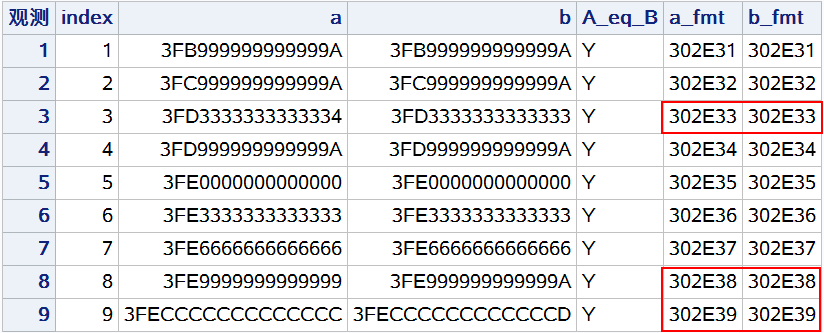
    a_fmt = put(a, 3.1);
    b_fmt = put(b, 3.1);
    if a_fmt = b_fmt then A_eq_B = "Y";
run;
proc print data = s3;
    var index a b A_eq_B a_fmt b_fmt;
    format a hex16. b hex16. a_fmt $hex16. b_fmt $hex16.;
run;

使用过程步中的选项

proc compare base = s1 compare = s2(rename = (b = a)) criterion = 0.1 method = absolute;
run;

参考文献：https://www.jianguoyun.com/p/DfN3qOQQ6YbXCRimmbME