基本相机模型及参数

1.相机模型

1.1基本针孔相机模型

如图:

空间中一点$M(X，Y，Z)$在图像平面上的投影点为$m((x_m,y_m,z_m)$,相机的焦距为$f$,对于理想真空相机模型可得如上的相似三角形$\Delta CmP\sim \Delta CM{M}^{\prime }$,则可得：
$\frac{Z}{f}=\frac{Y}{y_m}=\frac{X}{x_m}$
表示成矩阵形式为：

$Z\left[\begin{array}{c}{x}_m\\ y_m\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$

上图假设图像平面的原点在主点p上，实际情况可能并非如此，带偏置的一般场景为：

$\frac{Z}{f}=\frac{Y}{y_m-p_y}=\frac{X}{x_m-p_x}$

表示成矩阵形式为：

$Z\left[\begin{array}{c}{x}_m\\ y_m\\ 1\end{array}\right]=\left[\begin{array}{ccc}f& 0& p_x\\ 0& f& p_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$

由以上可求得世界坐标系中的点到图像平面的变换,考虑图像平面到像素平面的变换，可用如下表达式表示：

$\{\begin{array}{c}\mu =\frac{x_m}{\Delta x_m}+{\mu }_0\\ v=\frac{y_m}{\Delta y_m}+v_0\end{array}\to \left[\begin{array}{c}\mu \\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{\Delta x_m}& 0& {\mu }_0\\ 0& \frac{1}{\Delta y_m}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{x}_m\\ y_m\\ 1\end{array}\right]$
式中$\Delta x_m$、$\Delta y_m$表示在图像平面坐标系下$x$、$y$方向上每个像素的大小。由以上各式可得：

$Z\left[\begin{array}{c}\mu \\ v\\ 1\end{array}\right]=\left[\begin{array}{ccc}\frac{f_x}{\Delta x_m}& 0& {\mu }_0\\ 0& \frac{f_y}{\Delta y_m}& v_0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=K\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]$
其中，K为相机标定矩阵，常用张正友标定法通过棋盘格标定。但对于实际的相机由于制造工艺和安装位置误差
通常会导致径向和切向的畸变。常见的径向畸变有桶型失真和枕型失真，如下图:

在针孔相机模型中1，焦距$f$的概念指的是针孔到像平面的距离，与凸透镜的焦距有所不同，这里的像平面也即相机的感光器件所在的成像平面。焦距$f$越大，像平面上的物体图像也就越大;焦距$f$越小，像平面上所获得的物体图像越小，图像越清晰。另外，小孔的直径称为孔径，对应到真实相机也就是光圈直径。理想的小孔的直径是无穷小的，这当然是不可能的。孔径扩大，会导致传感器上的一个像素由多个场景点发出的光所贡献，因此会使得成像模糊。按照几何光学的理论，小孔做的越小越好，这样画面会变得更加清晰锐利，但是由于光的波粒二象性，一束波通过一个小孔后，会发生衍射现象，而且小孔越小，衍射现象越严重。孔径变为两倍，光能变大四倍。焦距变为两倍，光能变为四分之一。

相机镜头的光圈如图：

1.2凸透镜成像

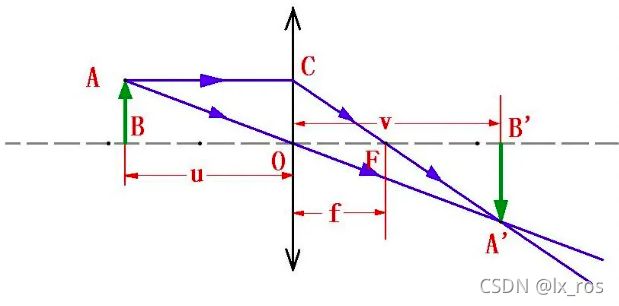
小孔成像模型是理想的基本相机模型，实际的成像系统是透镜成像的非线性模型。凸透镜成像的基本原理如图2：

有凸透镜成像公式：$\frac{1}{f}=\frac{1}{\mu }+\frac{1}{v}$，焦距的倒数等于像距与物距的倒数和。
数字相机的镜头相当于一个凸透镜，感光元件就处在这个凸透镜的焦点附近，将焦距近似为凸透镜中心到感光元件的距离时就简化成为了针孔成像模型。
对于相机来说，感光元器件所在的平面就是像平面，像平面通常在焦距附近,因为只有在焦平面附近能够较好成像。

以上讨论中，小孔和凸透镜都是理想模型，譬如平行光经过凸透镜后能汇聚到唯一的一个焦点。实际情况不是这样，平行光通过一个凸透镜，根本就不是汇聚到一个点，而是越靠近中轴线的光束聚焦得越远，越靠近透镜边缘的光聚焦得越近。如下图,引用自3：

2.相机相关参数和术语

2.1 变焦

变焦（Zoom）一词是指改变焦距f。只有变焦镜头的焦距才能被改变，定焦镜头的焦距是固定的。事实上，相机的镜头由多片凸透镜和凹透镜组成，但从成像结果来看，可以把这一组镜片看成“一个”凸透镜。这“一个”凸透镜的焦距就是标在镜头上的诸如定焦的50MM。那么变焦镜头比如18-55MM，怎么回事呢，说穿了很简单，就是改变这“一个”镜头里某些镜片的位置，达到改变这“一个”凸透镜的“凸的程度”，也就是焦距f。变焦最直观的体验就是被摄物体在取景器里被放大或者缩小了，调整相机视野的大小，焦距大视野小，焦距小视野大。

图片引用自4

2.3 对焦

对焦(Focus)一词习惯指改变像距v,也就是改变镜头光心到底片平面的距离。其基本原理是：通过相机镜头中镜片组的前后移动，改变像距的位置，使物像恰好落在底片或感光元件上。4除了一些低档傻瓜机镜头没有调焦机构，不能改变像距外，所有镜头，无论定焦变焦，都可以改变像距。当我们转动对焦环的时候，显然是某组镜片在前后移动，这组镜片动了以后，这“一个”镜头的“光心”就动了，物距和像距自然就动了,使其满足成像方程,获得清晰图像。

2.3 弥散圆

弥散圆，Circle of Confusion，在焦点前后，光线从聚集到扩散，点的影象从圆到点（焦点），继而有扩散到圆，这个焦点前面和后面的圆就叫做弥散圆。

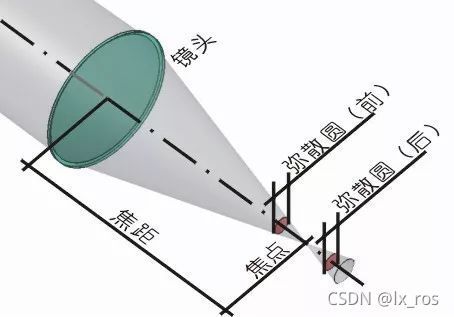
如果此圆形足够小，肉眼依然可被视为点的成像。这个可以被接受的最大直径被称为容许弥散圆直径δ (Permissible circle of confusion)。

观赏拍摄的影象是以某种方式来观察的，人的肉眼所感受到的影象与观看距离有很大的关系，如果弥散圆的直径小于人眼的鉴别能力，人眼将感觉是清晰的。这时的弥散圆的大小就称为容许弥散圆5。

2.4 景深

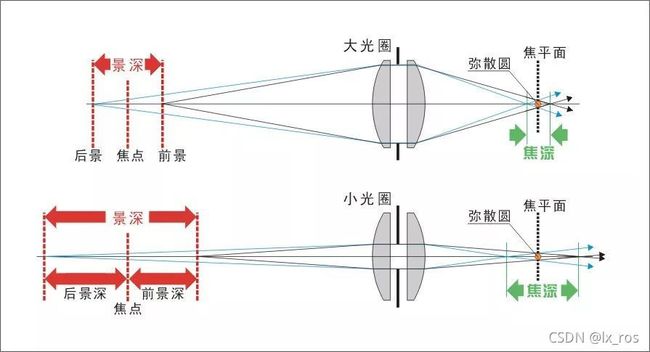
在对焦时，通过镜头将在焦平面上清晰成像，而对焦点的前景和后景也在焦平面成像，只要它们成像的弥散圆等于或小于容许弥散圆直径，我们将认为是清晰的，这样影像就有一个的清晰的区间，这就是景深（下图）：

从以上可知道，在焦点前后各有一个容许弥散圆，这两个弥散圆之间的距离我们称呼它叫焦深，它和景深是相对应的。焦距短，景深大。对焦点远，景深大。光圈小，景深大。

2.5 画幅

画幅究竟是什么意思？在胶片时代，画幅往往指的是相机在胶卷上成像范围的面积；也就是胶片的大小。而在数码时代，负责成像的并非胶卷，而是相机内部的图像传感器，因此如今我们常说的画幅通常是指传感器面积的大小。胶片的面积越大，成像的面积越大。同样，传感器的面积越大，成像的面积越大，像素越多越细腻，简单的说，画质越好6。

2.6 超焦距

在摄影镜头的焦距和光圈均已确定的前提下，能够获得最大景深时的摄影物距，称为在这个焦距和这个光圈下的超焦距。

2.7 白平衡

为了让白色的狗狗在昏黄的路灯的黄色光的照片里是白色的，那么就需要白平衡来调整色调。光的色调是通过色温来实现的，色温会告诉相机这些光是暖色调还是冷色调。色温说的是光线的温度，比如暖光或者冷光。色温的测量单位是开尔文，表示为K。冷光，色温高，偏蓝。暖光，色温低，偏红。暖光的色温低，偏红，冷光的色温高，偏蓝。比如在日出日落的时候，我们可能更希望突显这种美妙的黄昏色，需要使用色温低的暖色调。7

2.8 快门(曝光时间)

曝光时间是为了将光投射到照相感光材料的感光面上，快门所要打开的时间。快门是通过控制光线进入相机时间的长短，进而控制进光量的。相机中一般用1/400、8”这样的形式表示快门时间（也叫快门速度）。这个数值越大，快门开启的时间越长，进入相机的光线就越多；反之数值越小，进光量越少。8

快门时间长短直接影响进光量的多少。在光圈和感光度不变的情况下，快门时间越长，照片越亮，反之越暗。

如果你想抓拍美丽瞬间，那快门时间越短越好，这能让时间定格，拍的也清楚。如果你想记录轨迹或者过程，那一定要设置长快门

2.9 感光度ISO

感光度9又称为ISO，是指相机对光线的敏感程度。感光度，又称为ISO值，是衡量底片对于光的灵敏程度，由敏感度测量学及测量数个数值来决定，国际标准化组织标准为ISO 6。对于光较不敏感的底片，需要曝光更长的时间以达到跟较敏感底片相同的成像，因此通常被称为慢速底片。高度敏感的底片因而称为快速底片。基本上，使用较高的感光度，照片的品质较差。

2.10 分辨率

分辨率，相机每次采集图像的像素点数（Pixels），对于工业数字相机一般是直接与光电传感器的像元数对应的。目前工业数字相机像元尺寸一般为3μm-10μm，一般像元尺寸越小，制造难度越大，图像质量也越不容易提高。分辨率影响采集图像的质量，在对同样大的视场（景物范围）成像时，分辨率越高，对细节的展示越明显。
像素深度：每位像素数据的位数，常见的是8bit，10bit，12bit。分辨率和像素深度共同决定了图像的大小。例如对于像素深度为8bit的500万像素，则整张图片应该有500万*8/1024/1024=37M。10

2.11 靶面尺寸

CCD或CMOS相机光电转换器件的大小。镜头靶面尺寸要大于等于sensor传感器的对角线尺寸。11

2.12视场角(FOV)

在光学仪器中，以光学仪器的镜头为顶点，以被测目标的物像可通过镜头的最大范围的两条边缘构成的夹角，称为视场角。在显示系统中，视场角就是显示器边缘与观察点（眼睛）连线的夹角。12

参考:
1.https://zhuanlan.zhihu.com/p/95059112
2.https://baike.baidu.com/item/%E6%88%90%E5%83%8F%E5%85%AC%E5%BC%8F/506912
3.https://www.zhihu.com/question/33793912
4.https://www.sohu.com/a/422036567_116178
5.https://www.sohu.com/a/202227755_712214
6.https://zhuanlan.zhihu.com/p/55993337
7.https://zhuanlan.zhihu.com/p/56562780
8.https://www.zhihu.com/question/21427664
9.https://zh.wikipedia.org/wiki/%E6%84%9F%E5%85%89%E5%BA%A6
10.https://blog.csdn.net/baidu_35536188/article/details/109749171
11.https://www.zhihu.com/question/265008396
12.https://www.colorspace.com.cn/wiki/doc-view-716.html