深度学习相关概念:权重初始化
深度学习相关概念:权重初始化
- 1.全零初始化(×)
- 2.随机初始化
-
- 2.1 高斯分布/均匀分布
-
- 2.1.1权重较小— N ( 0 , 0.01 ) \pmb{\mathcal{N}(0,0.01)} N(0,0.01)N(0,0.01)N(0,0.01)
- 2.1.1权重较大— N ( 0 , 1 ) \pmb{\mathcal{N}(0,1)} N(0,1)N(0,1)N(0,1)
- 2.1.3存在问题:
- 2.2 Xavier初始化
-
- 2.2.1 原理
- 2.2.2 N ( 0 , 1 / N ) \pmb{\mathcal{N}(0,1 / N)} N(0,1/N)N(0,1/N)N(0,1/N)高斯分布
- 2.2.3 Xavier初始化局限性
- 2.3 He 初始化(MSRA)
- 3.权重初始化总结
权重初始化(weight initialization)又称参数初始化,在深度学习模型训练过程的本质是对weight(即参数 W)进行更新,但是在最开始训练的时候是无法更新的,这需要每个参数有相应的初始值。在进行权重初始化后,神经网络就可以对权重参数w不停地迭代更新,以达到较好的性能。
1.全零初始化(×)
全零初始化是我们要避免的,它无法训练网络。因为全零初始化后,神经网络训练时,在反向传播时梯度相同,参数更新大学也一样,最后会出现输出层两个权值相同,隐层神经元参数相同,也就是说神经网络失去了特征学习的能力。通俗点说,把神经网络比作你在爬山,但身处直线形的山谷中,两边是对称的山峰。如果全零初始化,由于对称性,你所在之处的梯度只能沿着山谷的方向,不会指向山峰;你走了一步之后,情况依然不变。结果就是你只能收敛到山谷中的一个极大值,而走不到山峰上去。
2.随机初始化
2.1 高斯分布/均匀分布
实验网络结构:10个隐层,1个输出层,每个隐层包含500个神经元,使用的双曲正切激活函数(tanh)。
2.1.1权重较小— N ( 0 , 0.01 ) \pmb{\mathcal{N}(0,0.01)} N(0,0.01)N(0,0.01)N(0,0.01)
除了前两层,后续所有层的激活值为0;此时,输入信息传递不到输出层;最终,网络得不到训练。小权重高斯初始化(小型网络中很常见),然而当网络越来越深的时候,会出现梯度消失的情况。
2.1.1权重较大— N ( 0 , 1 ) \pmb{\mathcal{N}(0,1)} N(0,1)N(0,1)N(0,1)

几乎所有的神经元都饱和了(不是-1就是1);前向传播时,神经元要么被抑制(0),要么被饱和(1)。此时,神经元局部梯度都是零,网络没有反向梯度流(梯度消失);最终,所有的参数得不到更新。
2.1.3存在问题:
随机初始化其实很难的,尝试太小的值,信息传不过去(2.1.1中权重分布都在0),值太大的时候梯度信息传递过去了,他们又进入了饱和区,梯度缺变成了0(2.1.2中权重不是1就是-1),虽然能让我的梯度传过来的每个成员的这个算的结果不一样,得出来的更新全值不一样但是很多时候能更新的机会都没有。在2.1.1的前项传播中,信息流消失;在2.1.2的反向传播中的梯度消失了,网络是没法训练的。
那到底怎么应该初始化呢?
有效的初始化方法:使网络各层的激活值和局部梯度的方差在传播过程中尽量保持一致;以保持网络中正向和反向数据流动。
2.2 Xavier初始化
2.2.1 原理
假设一个神经元, 其输入为 z 1 , z 2 , ⋯ z N z_{1}, z_{2}, \cdots z_{N} z1,z2,⋯zN, 这 N N N 个输入是独立同分布的; 其权值为 w 1 , … … , w N w_{1}, \ldots \ldots, w_{N} w1,……,wN, 它们也是独立同分布的,且 w w w 与 z z z 是独立的; 其激活函数为 f f f; 其最终输出 y y y 的表达式:
y = f ( w 1 ∗ z 1 + ⋯ + w N ∗ z N ) y=f\left(w_{1} * z_{1}+\cdots+w_{N} * z_{N}\right) y=f(w1∗z1+⋯+wN∗zN)
基本思想: 使网络各层的激活值和局部梯度的方差在传 播过程中尽量保持一致, 即寻找 w w w 的分布使得输 出 y \mathrm{y} y 与输入 z z z 的方差一致.
假设 f \pmb{f} fff 为双曲正切函数, w 1 , ⋯ , w N \pmb{w_{1}, \cdots, w_{N}} w1,⋯,wNw1,⋯,wNw1,⋯,wN 独立同分布, z 1 , ⋯ , z N \pmb{z_{1}, \cdots, z_{N}} z1,⋯,zNz1,⋯,zNz1,⋯,zN 独立同 分布, 随机变量w与 z z z 独立, 且均值都为 0 , 则有:
Var ( y ) = Var ( ∑ i = 1 N w i z i ) = ∑ i = 1 N Var ( w i z i ) = ∑ i N [ E ( w i ) ] 2 Var ( z i ) + [ E ( z i ) ] 2 Var ( w i ) + Var ( w i ) Var ( z i ) = ∑ i N Var ( w i ) Var ( z i ) = N Var ( w i ) Var ( z i ) \begin{aligned} \operatorname{Var}(y) &=\operatorname{Var}\left(\sum_{i=1}^{N} w_{i} z_{i}\right)=\sum_{i=1}^{N} \operatorname{Var}\left(w_{i} z_{i}\right) \\ &=\sum_{i}^{N}\left[E\left(w_{i}\right)\right]^{2} \operatorname{Var}\left(\mathrm{z}_{i}\right)+\left[E\left(z_{i}\right)\right]^{2} \operatorname{Var}\left(w_{i}\right)+\operatorname{Var}\left(w_{i}\right) \operatorname{Var}\left(z_{i}\right) \\ &=\sum_{i}^{N} \operatorname{Var}\left(w_{i}\right) \operatorname{Var}\left(z_{i}\right) \\ &=N\operatorname{Var}\left(\mathrm{w}_{i}\right) \operatorname{Var}\left(z_{i}\right) \end{aligned} Var(y)=Var(i=1∑Nwizi)=i=1∑NVar(wizi)=i∑N[E(wi)]2Var(zi)+[E(zi)]2Var(wi)+Var(wi)Var(zi)=i∑NVar(wi)Var(zi)=NVar(wi)Var(zi)
当且仅当 var ( w ) = 1 / N \pmb{\operatorname{var}(w)=1 / N} var(w)=1/Nvar(w)=1/Nvar(w)=1/N 时, y \pmb{y} yyy 的方差与 z \pmb{z} zzz 的方差一致。因此我们可以采用 N ( 0 , 1 / N ) \pmb{\mathcal{N}(0,1 / N)} N(0,1/N)N(0,1/N)N(0,1/N)的高斯分布,为输入神经元个数。
2.2.2 N ( 0 , 1 / N ) \pmb{\mathcal{N}(0,1 / N)} N(0,1/N)N(0,1/N)N(0,1/N)高斯分布
Xavier初始化可以帮助减少梯度消失的问题,使得信号在神经网络中可以传递得更深,在经过多层神经元后保持在合理的范围。每层神经元激活值的方差基本相同。符合正态分布,这样前向的信息流可以传递,反向传播梯度也可以更新。

2.2.3 Xavier初始化局限性
Xavier初始化能够很好的 tanh 激活函数。但是对于目前最常用的 ReLU 激活函数,Xavier初始化表现的很差。

在较浅的层中效果还不错,但是随着神经网络层数的增加,权重趋势却是越来越接近0。
那如何解决ReLU激活函数的初始化?
采用恺明初始化(He 初始化)
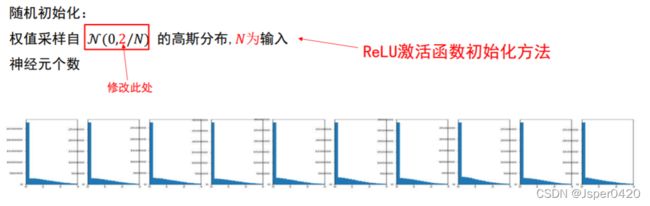
2.3 He 初始化(MSRA)
He 初始化(MSRA)与Xavier初始化不同在哪里?
Xavier初始化采用的是 N ( 0 , 1 / N ) \pmb{\mathcal{N}(0,1 / N)} N(0,1/N)N(0,1/N)N(0,1/N)高斯分布,He 初始化(MSRA)采用的是 N ( 0 , 2 / N ) \pmb{\mathcal{N}(0,2 / N)} N(0,2/N)N(0,2/N)N(0,2/N)高斯分布。
He 初始化(MSRA)原理:
在ReLU网络中,假定每一层有一半的神经元被激活,另一半为0(x负半轴中是不激活的),所以要保持variance不变,只需要在Xavier的基础上再除以2:
3.权重初始化总结
-
好的初始化方法可以防止前向传播过程中的信息消失,也可以解决反向传递过程中的梯度消失。
-
激活函数选择双曲正切或者Sigmoid时,建议使用Xaizer初始化方法。
-
激活函数选择ReLU或Leakly ReLU时,推荐使用He初始化方法。


