PyTorch学习笔记（三）：PyTorch主要组成模块

往期学习资料推荐： 

1.Pytorch实战笔记_GoAI的博客-CSDN博客

2.Pytorch入门教程_GoAI的博客-CSDN博客

本系列目录：

PyTorch学习笔记（一）：PyTorch环境安装

PyTorch学习笔记（二）：简介与基础知识

PyTorch学习笔记（三）：PyTorch主要组成模块

PyTorch学习笔记（四）：PyTorch基础实战

PyTorch学习笔记（五）：模型定义、修改、保存

后续继续更新！！！！

1 深度学习步骤

（1）数据预处理：通过专门的数据加载，通过批训练提高模型表现，每次训练读取固定数量的样本输入到模型中进行训练
（2）深度神经网络搭建：逐层搭建，实现特定功能的层（如积层、池化层、批正则化层、LSTM层等）
（3）损失函数和优化器的设定：保证反向传播能够在用户定义的模型结构上实现
（4）模型训练：使用并行计算加速训练，将数据按批加载，放入GPU中训练，对损失函数反向传播回网络最前面的层，同时使用优化器调整网络参数

2 基本配置

• 导入相关的包

import os
import numpy as py
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
import torch.optim as optimizer

• 统一设置超参数：batch size、初始学习率、训练次数、GPU配置

# set batch size
batch_size = 16

# 初始学习率
lr = 1e-4

# 训练次数
max_epochs = 100

# 配置GPU
device = torch.device("cuda:1" if torch.cuda.is_available() else "cpu")
device

device(type='cuda', index=1)

3 数据读入

• 读取方式：通过Dataset+DataLoader的方式加载数据，Dataset定义好数据的格式和数据变换形式，DataLoader用iterative的方式不断读入批次数据。

• 自定义Dataset类：实现__init___、__getitem__、__len__函数

• torch.utils.data.DataLoader参数：

  1. batch_size：样本是按“批”读入的，表示每次读入的样本数
  2. num_workers：表示用于读取数据的进程数
  3. shuffle：是否将读入的数据打乱
  4. drop_last：对于样本最后一部分没有达到批次数的样本，使其不再参与训练

4 模型构建

4.1 神经网络的构造

通过Module类构造模型，实例化模型之后，可完成模型构造

# 构造多层感知机
class MLP(nn.Module):
    def __init__(self, **kwargs):
        super(MLP, self).__init__(**kwargs)
        self.hidden = nn.Linear(784, 256)
        self.act = nn.ReLU()
        self.output = nn.Linear(256, 10)
        
    def forward(self, X):
        o = self.act(self.hidden(x))
        return self.output(o)

x = torch.rand(2, 784)
net = MLP()
print(x)
net(x)

tensor([[0.8924, 0.9624, 0.3262,  ..., 0.8376, 0.1889, 0.9060],
        [0.3609, 0.8005, 0.5175,  ..., 0.6255, 0.1462, 0.9846]])





tensor([[-0.0902,  0.0199,  0.0677, -0.0679,  0.0799,  0.0826,  0.0628,  0.1809,
         -0.2387,  0.0366],
        [-0.2271,  0.0056, -0.0984, -0.0432, -0.0160, -0.0038,  0.0953,  0.0545,
         -0.1530, -0.0214]], grad_fn=)

4.2 神经网络常见的层

• 不含模型参数的层

# 构造一个输入减去均值后输出的层
class MyLayer(nn.Module):
    def __init__(self, **kwargs):
        super(MyLayer, self).__init__(**kwargs)
    
    def forward(self, x):
        return x - x.mean()
x = torch.tensor([0, 5, 10, 15, 20], dtype=torch.float)
layer = MyLayer()
layer(x)

tensor([-10.,  -5.,   0.,   5.,  10.])

• 含模型参数的层：如果一个Tensor是Parameter，那么它会⾃动被添加到模型的参数列表里

# 使用ParameterList定义参数的列表
class MyListDense(nn.Module):
    def __init__(self):
        super(MyListDense, self).__init__()
        self.params = nn.ParameterList(
            [nn.Parameter(torch.randn(4, 4)) for i in range(3)])
        self.params.append(nn.Parameter(torch.randn(4, 1)))

    def forward(self, x):
        for i in range(len(self.params)):
            x = torch.mm(x, self.params[i])
        return x
net = MyListDense()
print(net)

MyListDense(
  (params): ParameterList(
      (0): Parameter containing: [torch.FloatTensor of size 4x4]
      (1): Parameter containing: [torch.FloatTensor of size 4x4]
      (2): Parameter containing: [torch.FloatTensor of size 4x4]
      (3): Parameter containing: [torch.FloatTensor of size 4x1]
  )
)

# 使用ParameterDict定义参数的字典
class MyDictDense(nn.Module):
    def __init__(self):
        super(MyDictDense, self).__init__()
        self.params = nn.ParameterDict({
                'linear1': nn.Parameter(torch.randn(4, 4)),
                'linear2': nn.Parameter(torch.randn(4, 1))
        })
        # 新增参数linear3
        self.params.update({'linear3': nn.Parameter(torch.randn(4, 2))}) 

    def forward(self, x, choice='linear1'):
        return torch.mm(x, self.params[choice])

net = MyDictDense()
print(net)

MyDictDense(
  (params): ParameterDict(
      (linear1): Parameter containing: [torch.FloatTensor of size 4x4]
      (linear2): Parameter containing: [torch.FloatTensor of size 4x1]
      (linear3): Parameter containing: [torch.FloatTensor of size 4x2]
  )
)

• 二维卷积层：使用nn.Conv2d类构造，模型参数包括卷积核和标量偏差，在训练模式时，通常先对卷积核随机初始化，再不断迭代卷积核和偏差

# 计算卷积层，对输入和输出做相应的升维和降维
def comp_conv2d(conv2d, X):
    # (1, 1)代表批量大小和通道数
    X = X.view((1, 1) + X.shape)
    Y = conv2d(X)
    # 排除不关心的前两维：批量和通道
    return Y.view(Y.shape[2:]) 
# 注意这里是两侧分别填充1⾏或列，所以在两侧一共填充2⾏或列
conv2d = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=3,padding=1)

X = torch.rand(8, 8)
comp_conv2d(conv2d, X).shape

torch.Size([8, 8])

• 池化层：直接计算池化窗口内元素的最大值或者平均值，分别叫做最大池化或平均池化

# 二维池化层
def pool2d(X, pool_size, mode='max'):
    p_h, p_w = pool_size
    Y = torch.zeros((X.shape[0] - p_h + 1, X.shape[1] - p_w + 1))
    for i in range(Y.shape[0]):
        for j in range(Y.shape[1]):
            if mode == 'max':
                Y[i, j] = X[i: i + p_h, j: j + p_w].max()
            elif mode == 'avg':
                Y[i, j] = X[i: i + p_h, j: j + p_w].mean()
    return Y
X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]], dtype=torch.float)
pool2d(X, (2, 2), 'max')

tensor([[4., 5.],
        [7., 8.]])

pool2d(X, (2, 2), 'avg')

tensor([[2., 3.],
        [5., 6.]])

4.3 模型示例

• 神经网络训练过程：

  1. 定义可学习参数的神经网络
  2. 在输入数据集上进行迭代训练
  3. 通过神经网络处理输入数据
  4. 计算loss（损失值）
  5. 将梯度反向传播给神经网络参数
  6. 更新网络参数，使用梯度下降

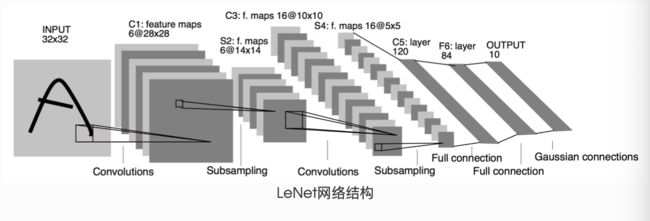
• LeNet(前馈神经网络) 

  ​

import torch.nn.functional as F

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        # 输入图像channel是1；输出channel是6；5x5卷积核
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # 2x2 Max pooling
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # 如果是方阵,则可以只使用一个数字进行定义
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        # 除去批处理维度的其他所有维度
        size = x.size()[1:]  
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
net

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

# 假设输入的数据为随机的32x32
input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)

tensor([[-0.0921, -0.0605, -0.0726, -0.0451,  0.1399, -0.0087,  0.1075,  0.0799,
         -0.1472,  0.0288]], grad_fn=)

# 清零所有参数的梯度缓存，然后进行随机梯度的反向传播
net.zero_grad()
out.backward(torch.randn(1, 10))

• AlexNet  

class AlexNet(nn.Module):
    def __init__(self):
        super(AlexNet, self).__init__()
        self.conv = nn.Sequential(
            # in_channels, out_channels, kernel_size, stride, padding
            nn.Conv2d(1, 96, 11, 4), 
            nn.ReLU(),
            # kernel_size, stride
            nn.MaxPool2d(3, 2), 
            # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
            nn.Conv2d(96, 256, 5, 1, 2),
            nn.ReLU(),
            nn.MaxPool2d(3, 2),
            # 连续3个卷积层，且使用更小的卷积窗口。
            # 除了最后的卷积层外，进一步增大了输出通道数。
            # 前两个卷积层后不使用池化层来减小输入的高和宽
            nn.Conv2d(256, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 384, 3, 1, 1),
            nn.ReLU(),
            nn.Conv2d(384, 256, 3, 1, 1),
            nn.ReLU(),
            nn.MaxPool2d(3, 2)
        )
         # 这里全连接层的输出个数比LeNet中的大数倍。使用丢弃层来缓解过拟合
        self.fc = nn.Sequential(
            nn.Linear(256*5*5, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(),
            nn.Dropout(0.5),
            # 输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
            nn.Linear(4096, 10),
        )

    def forward(self, img):
        feature = self.conv(img)
        output = self.fc(feature.view(img.shape[0], -1))
        return output
net = AlexNet()
print(net)

AlexNet(
  (conv): Sequential(
    (0): Conv2d(1, 96, kernel_size=(11, 11), stride=(4, 4))
    (1): ReLU()
    (2): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (3): Conv2d(96, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))
    (4): ReLU()
    (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
    (6): Conv2d(256, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (7): ReLU()
    (8): Conv2d(384, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (9): ReLU()
    (10): Conv2d(384, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
    (11): ReLU()
    (12): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)
  )
  (fc): Sequential(
    (0): Linear(in_features=6400, out_features=4096, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.5, inplace=False)
    (3): Linear(in_features=4096, out_features=4096, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.5, inplace=False)
    (6): Linear(in_features=4096, out_features=10, bias=True)
  )
)

5 损失函数

• 二分类交叉熵损失函数：torch.nn.BCELoss，用于计算二分类任务时的交叉熵

m = nn.Sigmoid()
loss = nn.BCELoss()
input = torch.randn(3, requires_grad=True)
target = torch.empty(3).random_(2)

output = loss(m(input), target)
output.backward()
print('BCE损失函数的计算结果:',output)

BCE损失函数的计算结果: tensor(0.9389, grad_fn=)

• 交叉熵损失函数：torch.nn.CrossEntropyLoss，用于计算交叉熵

loss = nn.CrossEntropyLoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)

output = loss(input, target)
output.backward()
print('CrossEntropy损失函数的计算结果:',output)

CrossEntropy损失函数的计算结果: tensor(2.7367, grad_fn=)

• L1损失函数：torch.nn.L1Loss，用于计算输出y和真实值target之差的绝对值

loss = nn.L1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)

output = loss(input, target)
output.backward()
print('L1损失函数的计算结果:',output)

L1损失函数的计算结果: tensor(1.0351, grad_fn=)

• MSE损失函数：torch.nn.MSELoss，用于计算输出y和真实值target之差的平方

loss = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)

output = loss(input, target)
output.backward()
print('MSE损失函数的计算结果:',output)

MSE损失函数的计算结果: tensor(1.7612, grad_fn=)

• 平滑L1（Smooth L1）损失函数：torch.nn.SmoothL1Loss，用于计算L1的平滑输出，减轻离群点带来的影响，通过与L1损失的比较，在0点的尖端处，过渡更为平滑

loss = nn.SmoothL1Loss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)

output = loss(input, target)
output.backward()
print('Smooth L1损失函数的计算结果:',output)

Smooth L1损失函数的计算结果: tensor(0.7252, grad_fn=)

• 目标泊松分布的负对数似然损失：torch.nn.PoissonNLLLoss

loss = nn.PoissonNLLLoss()
log_input = torch.randn(5, 2, requires_grad=True)
target = torch.randn(5, 2)

output = loss(log_input, target)
output.backward()
print('PoissonNL损失函数的计算结果:',output)

PoissonNL损失函数的计算结果: tensor(1.7593, grad_fn=)

• KL散度：torch.nn.KLDivLoss，用于连续分布的距离度量，可用在对离散采用的连续输出空间分布的回归场景

inputs = torch.tensor([[0.5, 0.3, 0.2], [0.2, 0.3, 0.5]])
target = torch.tensor([[0.9, 0.05, 0.05], [0.1, 0.7, 0.2]], dtype=torch.float)
loss = nn.KLDivLoss(reduction='batchmean')

output = loss(inputs,target)
print('KLDiv损失函数的计算结果:',output)

KLDiv损失函数的计算结果: tensor(-1.0006)

• MarginRankingLoss：torch.nn.MarginRankingLoss，用于计算两组数据之间的差异（相似度），可使用在排序任务的场景

loss = nn.MarginRankingLoss()
input1 = torch.randn(3, requires_grad=True)
input2 = torch.randn(3, requires_grad=True)
target = torch.randn(3).sign()

output = loss(input1, input2, target)
output.backward()
print('MarginRanking损失函数的计算结果:',output)

MarginRanking损失函数的计算结果: tensor(1.1762, grad_fn=)

• 多标签边界损失函数：torch.nn.MultiLabelMarginLoss，用于计算多标签分类问题的损失

loss = nn.MultiLabelMarginLoss()
x = torch.FloatTensor([[0.9, 0.2, 0.4, 0.8]])
# 真实的分类是，第3类和第0类
y = torch.LongTensor([[3, 0, -1, 1]])

output = loss(x, y)
print('MultiLabelMargin损失函数的计算结果:',output)

MultiLabelMargin损失函数的计算结果: tensor(0.4500)

• 二分类损失函数：torch.nn.SoftMarginLoss，用于计算二分类的logistic损失

# 定义两个样本，两个神经元
inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]])  
target = torch.tensor([[-1, 1], [1, -1]], dtype=torch.float)  

# 该loss对每个神经元计算，需要为每个神经元单独设置标签
loss_f = nn.SoftMarginLoss()
output = loss_f(inputs, target)
print('SoftMargin损失函数的计算结果:',output)

SoftMargin损失函数的计算结果: tensor(0.6764)

• 多分类的折页损失函数：torch.nn.MultiMarginLoss，用于计算多分类问题的折页损失

inputs = torch.tensor([[0.3, 0.7], [0.5, 0.5]]) 
target = torch.tensor([0, 1], dtype=torch.long) 

loss_f = nn.MultiMarginLoss()
output = loss_f(inputs, target)
print('MultiMargin损失函数的计算结果:',output)

MultiMargin损失函数的计算结果: tensor(0.6000)

• 三元组损失函数：torch.nn.TripletMarginLoss，用于处理<实体1，关系，实体2>类型的数据，计算该类型数据的损失

triplet_loss = nn.TripletMarginLoss(margin=1.0, p=2)
anchor = torch.randn(100, 128, requires_grad=True)
positive = torch.randn(100, 128, requires_grad=True)
negative = torch.randn(100, 128, requires_grad=True)

output = triplet_loss(anchor, positive, negative)
output.backward()
print('TripletMargin损失函数的计算结果:',output)

TripletMargin损失函数的计算结果: tensor(1.1507, grad_fn=)

• HingEmbeddingLoss：torch.nn.HingeEmbeddingLoss，用于计算输出的embedding结果的Hing损失

loss_f = nn.HingeEmbeddingLoss()
inputs = torch.tensor([[1., 0.8, 0.5]])
target = torch.tensor([[1, 1, -1]])

output = loss_f(inputs,target)
print('HingEmbedding损失函数的计算结果:',output)

HingEmbedding损失函数的计算结果: tensor(0.7667)

• 余弦相似度：torch.nn.CosineEmbeddingLoss，用于计算两个向量的余弦相似度，如果两个向量距离近，则损失函数值小，反之亦然

loss_f = nn.CosineEmbeddingLoss()
inputs_1 = torch.tensor([[0.3, 0.5, 0.7], [0.3, 0.5, 0.7]])
inputs_2 = torch.tensor([[0.1, 0.3, 0.5], [0.1, 0.3, 0.5]])
target = torch.tensor([1, -1], dtype=torch.float)

output = loss_f(inputs_1,inputs_2,target)
print('CosineEmbedding损失函数的计算结果:',output)

CosineEmbedding损失函数的计算结果: tensor(0.5000)

• CTC损失函数：torch.nn.CTCLoss，用于处理时序数据的分类问题，计算连续时间序列和目标序列之间的损失

# Target are to be padded
# 序列长度
T = 50      
# 类别数（包括空类）
C = 20      
# batch size
N = 16
# Target sequence length of longest target in batch (padding length)
S = 30      
# Minimum target length, for demonstration purposes
S_min = 10  

input = torch.randn(T, N, C).log_softmax(2).detach().requires_grad_()
# 初始化target(0 = blank, 1:C = classes)
target = torch.randint(low=1, high=C, size=(N, S), dtype=torch.long)

input_lengths = torch.full(size=(N,), fill_value=T, dtype=torch.long)
target_lengths = torch.randint(low=S_min, high=S, size=(N,), dtype=torch.long)

ctc_loss = nn.CTCLoss()
loss = ctc_loss(input, target, input_lengths, target_lengths)
loss.backward()
print('CTC损失函数的计算结果:',loss)

CTC损失函数的计算结果: tensor(6.1333, grad_fn=)

6 优化器

6.1 Optimizer的属性和方法

• 使用方向：为了使求解参数过程更快，使用BP+优化器逼近求解

• Optimizer的属性：

  • defaults：优化器的超参数
  • state：参数的缓存
  • param_groups：参数组，顺序是params，lr，momentum，dampening，weight_decay，nesterov

• Optimizer的方法：

  • zero_grad()：清空所管理参数的梯度
  • step()：执行一步梯度更新
  • add_param_group()：添加参数组
  • load_state_dict()：加载状态参数字典，可以用来进行模型的断点续训练，继续上次的参数进行训练
  • state_dict()：获取优化器当前状态信息字典

6.2 基本操作

# 设置权重，服从正态分布  --> 2 x 2
weight = torch.randn((2, 2), requires_grad=True)

# 设置梯度为全1矩阵  --> 2 x 2
weight.grad = torch.ones((2, 2))

# 输出现有的weight和data
print("The data of weight before step:\n{}".format(weight.data))
print("The grad of weight before step:\n{}".format(weight.grad))

The data of weight before step:
tensor([[-0.5871, -1.1311],
        [-1.0446,  0.2656]])
The grad of weight before step:
tensor([[1., 1.],
        [1., 1.]])

# 实例化优化器
optimizer = torch.optim.SGD([weight], lr=0.1, momentum=0.9)

# 进行一步操作
optimizer.step()

# 查看进行一步后的值，梯度
print("The data of weight after step:\n{}".format(weight.data))
print("The grad of weight after step:\n{}".format(weight.grad))

The data of weight after step:
tensor([[-0.6871, -1.2311],
        [-1.1446,  0.1656]])
The grad of weight after step:
tensor([[1., 1.],
        [1., 1.]])

# 权重清零
optimizer.zero_grad()

# 检验权重是否为0
print("The grad of weight after optimizer.zero_grad():\n{}".format(weight.grad))

The grad of weight after optimizer.zero_grad():
tensor([[0., 0.],
        [0., 0.]])

# 添加参数：weight2
weight2 = torch.randn((3, 3), requires_grad=True)
optimizer.add_param_group({"params": weight2, 'lr': 0.0001, 'nesterov': True})

# 查看现有的参数
print("optimizer.param_groups is\n{}".format(optimizer.param_groups))

# 查看当前状态信息
opt_state_dict = optimizer.state_dict()
print("state_dict before step:\n", opt_state_dict)

optimizer.param_groups is
[{'params': [tensor([[-0.6871, -1.2311],
        [-1.1446,  0.1656]], requires_grad=True)], 'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False}, {'params': [tensor([[ 0.0411, -0.6569,  0.7445],
        [-0.7056,  1.1146, -0.4409],
        [-0.2302, -1.1507, -1.3807]], requires_grad=True)], 'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0}]
state_dict before step:
 {'state': {0: {'momentum_buffer': tensor([[1., 1.],
        [1., 1.]])}}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}, {'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'params': [1]}]}

# 进行5次step操作
for _ in range(50):
    optimizer.step()
# 输出现有状态信息
print("state_dict after step:\n", optimizer.state_dict())

state_dict after step:
 {'state': {0: {'momentum_buffer': tensor([[0.0052, 0.0052],
        [0.0052, 0.0052]])}}, 'param_groups': [{'lr': 0.1, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'nesterov': False, 'params': [0]}, {'lr': 0.0001, 'nesterov': True, 'momentum': 0.9, 'dampening': 0, 'weight_decay': 0, 'params': [1]}]}

7 训练与评估

def train(epoch):
    # 设置训练状态
    model.train()
    train_loss = 0
    # 循环读取DataLoader中的全部数据
    for data, label in train_loader:
        # 将数据放到GPU用于后续计算
        data, label = data.cuda(), label.cuda()
        # 将优化器的梯度清0
        optimizer.zero_grad()
        # 将数据输入给模型
        output = model(data)
        # 设置损失函数
        loss = criterion(label, output)
        # 将loss反向传播给网络
        loss.backward()
        # 使用优化器更新模型参数
        optimizer.step()
        # 累加训练损失
        train_loss += loss.item()*data.size(0)
    train_loss = train_loss/len(train_loader.dataset)
    print('Epoch: {} \tTraining Loss: {:.6f}'.format(epoch, train_loss))

def val(epoch):  
    # 设置验证状态
    model.eval()
    val_loss = 0
    # 不设置梯度
    with torch.no_grad():
        for data, label in val_loader:
            data, label = data.cuda(), label.cuda()
            output = model(data)
            preds = torch.argmax(output, 1)
            loss = criterion(output, label)
            val_loss += loss.item()*data.size(0)
            # 计算准确率
            running_accu += torch.sum(preds == label.data)
    val_loss = val_loss/len(val_loader.dataset)
    print('Epoch: {} \tTraining Loss: {:.6f}'.format(epoch, val_loss))