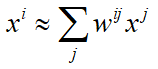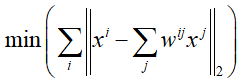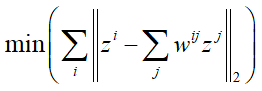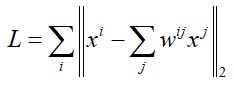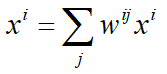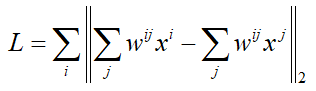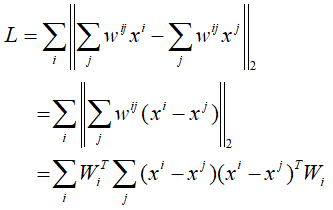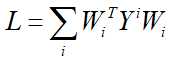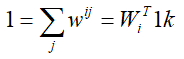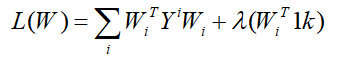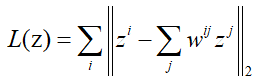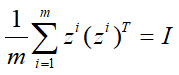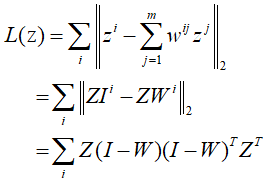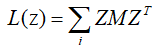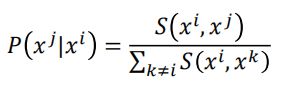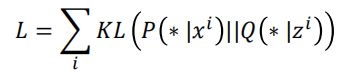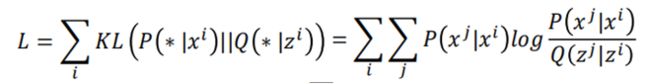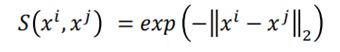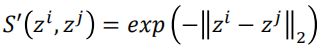【机器学习基础】无监督学习（2）——降维之LLE和TSNE

在上一节介绍了一种最常见的降维方法PCA，本节介绍另一种降维方法LLE，本来打算对于其他降维算法一并进行一个简介，不过既然看到这里了，就对这些算法做一个相对详细的学习吧。

---

0.流形学习简介

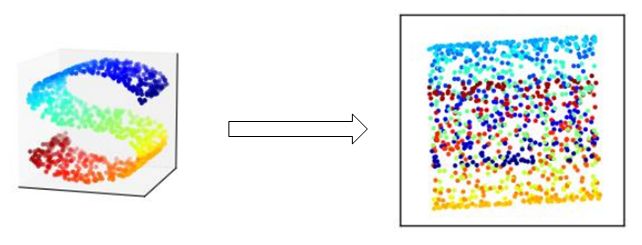
在前面PCA中说到，PCA是一种无法将数据进行拉直，当直接对于曲面进行降维后，导致数据的重叠，难以区分，如下图所示：

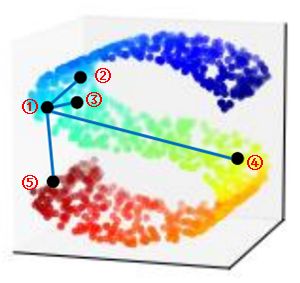
这是因为在使用PCA降维时，PCA仅仅关注于保持降维后的方差最大，没有考虑样本的局部特征，如图所示：

利用PCA在对点①进行降维后，没有考虑点①与其他点②、③、④..的位置关系，也就是说对于点①来说，点⑤到点①的距离相较于点④到点①的距离更近，而在实际中并非如此，有句话说叫“举头见日，不见长安”。

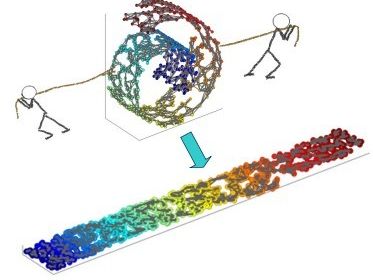
        此时就需要流形学习（Manifold Learning）来解决这个问题。所谓流形学习，就是一类基于流形的学习框架，所谓流形就是上面那样一张“S”的曲面，也可以想象成一个将地毯卷起来的样子，也就是一种不闭合的曲面，而流形学习就是对这个不闭合的去年进行降维，也就相当于把这上面那个“S”拉直，或者把地毯铺开的一个过程。

不同于PCA算法，流形学习在降维中关注保持样本的局部线性特征，为了保持局部特征，在进行降维时，不能将欧氏距离作为样本间的距离了，

此时就需要利用测地距离来保持样本间的特征，这个算法就是ISOMAP等距映射算法，该算法考虑在降维后每一个样本与其它样本的测地距离。

但ISOMAP也有一个问题，就是它要考虑所有其他样本之间的测地距离，当样本的数量巨大时，算法时间较长。这时就需要对算法做进一步的改进。

1.LLE

1.1 LLE简介及基本思想

         LLE（Local Linear Embedding）就是一种流形学习的算法，LLE在降维时不再考虑全部的样本来寻找全局最优解（这个在进行最终求解还是要考虑全局的，只不过对于每个样本而言，仅考虑局部），

而是保留局部的一些样本点作为局部特征进行降维，这样既保留了局部特征，又减少了计算量。

LLE的基本思想比较简单，也就是只考虑“最近几个样本点”进行降维，下面具体来说说LLE的思想：

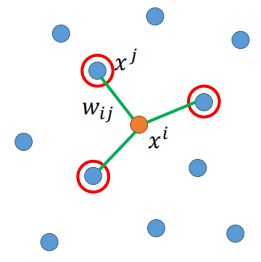
样本在原始空间中，分布如图所示：

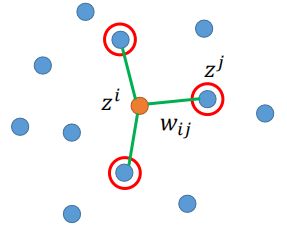
假设现在我们对xⁱ进行降维，将xⁱ从原始空间降到低维空间，降维后暂且在这里称之为zⁱ。

首先第一步，找出能够“代表”xⁱ的一些点，比如利用k-NN的方法，找到距离xⁱ的最近的点x^j.(注意：这里x^j并不是一个点，而是“一些”点）；

然后，定义这些能够“代表”xⁱ的这些点与x^j相连的权重为w^ij，那么xⁱ就可以用这些能够“代表”它的点进行表示为：

但这些也仅仅代表而已，并不真正相等，但我们希望越能够“代表”越好，也就是期望两个值越接近越好。

这是对于一个样本点i，而对于空间中所有的点都是如此，并且希望每一个样本点与能够“代表”它的那些点的越接近越好，也就是：

我们已经通过K-NN找出这些点x^j了,那对于w还是未知的，因此，需要找出一组w，使得上面的那个式子的值越小越好。这不就是一个常规的NN算法吗？直接使用梯度下降进行求解就可以求出w了。

现在假设我们已经求出了一组w，然后用这组w进行降维，同样，假设降维后的数据分布如下图：

这里zⁱ就是xⁱ从原始空间降维后的结果，保持w^ij不变，找一组zⁱ和z^j，使得：

可以看出，这个式子与上面的式子完全一样，不同的是，这里我们所要寻找的是zⁱ和z^j，而上面的式子所要寻找的是权重w^ij,这里同样利用梯度下降就可以进行优化求解。

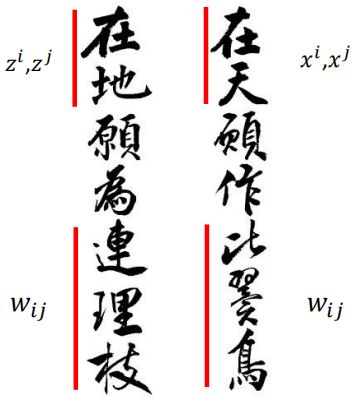
上面就是LLE的基本原理，其实LLE的原理从上面来看是比较简单的，为保持局部样本的特点，将样本用局部其他样本的线性表示然后进行降维。这种方法在李宏毅老师的课程里用一句比较形象的话来概括：

1.2 LLE的数学推导

上面介绍了LLE的基本原理，说到了对于降维的过程直接用梯度下降的方法进行优化求解即可，然而同PCA一样，LLE也有一套完整的推导流程。

前面对于PCA是基于数学推导流程，求出的解析解，然后说道PCA可以看做一个NN结构，利用梯度下降进行求解。

本打算这里不再对LLE的推导进行阐述，但看到目前sklearn下对LLE用的就是解析解的方法，这里就对LLE推导和求解过程进行一个简单的学习和推导。

• 首先，对于第一步寻找xⁱ的最近邻样本x^j这里就不再赘述，直接采用K-NN算法找出就可以了。
• 假设原始空间中有m个样本，每个样本为n维，假设样本xⁱ的近邻样本x^j有k个。

接下来，在高维空间中，需要找出xⁱ与x^j的空间线性关系，也就是找出权重系数w^ij。损失函数前面已经给出：

这里一般会对权重系数做一个归一化的处理，也就是：

为了便于推导，根据上面的归一化对xⁱ做一个变形：

则有：

作进一步的变换：

这里，然后令，则有：

再对约束条件进一步变形：

这里"1k"表示k*1全为1的向量。

根据损失函数L和约束条件，利用拉格朗日乘子求最小值：

对W进行求导，令其为0，则得到：

这里就得到了在高维空间中的权重系数。

这里W_i是一个k维的列向量，将所有样本的W_i串起来后，最终W则是一个m*k维的矩阵。

• 接下来根据这些权重系数，在低维空间中找出降维后的数据，使得下面的损失函数越小越好：

这里zⁱ和z^j是新的空间中的数据，也就是说原数据为m*n，到新空间中假设降到d维，则新空间数据变为m*d。

为了方便后边的推导，这里需要注意的是，这里的j不再是1~k，而是1~m，也就是说，从m个数据中拿出对应的k个样本，对于不属于近邻内的w则为0，也就是说，

W由原来的m*k维扩充到了m*m维，这里同样对于标准化数据有闲置条件：

对损失函数L(z)进一步整理得到：

令M=，则:

这里就类似于PCA中降维的求解过程类似（在PCA中是使其最大），同样的，对于上面的式子，使得L(z)最小的解为M的前d个最小的特征值所组成的特征向量所组成的Z。

这里注意的是，M的最小特征值为0，此时对应的特征向量为全1，不能反映数据特征，通常选择第2到d+1小的特征值对应的特征向量得到最终降维后的数据Z。

1.3 LLE的算法实现

根据上面的理论部分，按照其解析解的方式对LLE的算法进行实现，加深算法的理解。然后根据sklearn中的manifold中的LLE方法，实现LLE。

首先是LLE算法的具体实现过程：

import numpy as np


def cal_pairwise_dist(x):
    # 输入矩阵x，返回两两之间的距离
    """
    输入矩阵x，返回两两之间的距离
    (a-b)^2 = a^2 + b^2 - 2ab
    """
    # a^2 + b^2
    sum_x = np.sum(np.square(x), axis=1)

    dist = np.add(np.add(-2 * np.dot(x, x.T), sum_x).T, sum_x)
    return dist


def get_n_neighbors(data, n_neighbors=10):
    dist = cal_pairwise_dist(data)
    dist[dist < 0] = 0
    dist = dist ** 0.5

    n = dist.shape[0]
    N = np.zeros((n, n_neighbors))

    for i in range(n):
        # 计算每一个样本点，距离其最近的近邻点的索引
        index_ = np.argsort(dist[i])[1:n_neighbors+1]
        # 距离每一个样本最近的点的索引i
        N[i] = N[i] + index_

    return N.astype(np.int32)


def lle(data, n_dims=2, n_neighbors=10):
    # 先获取到样本点的近邻的样本索引
    N = get_n_neighbors(data, n_neighbors)
    # 样本数量n，维数为D
    n, D = data.shape

    # 当原空间维度小于近邻点数量时，W不是满秩的，要进行特殊处理
    if n_neighbors > D:
        tol = 1e-3
    else:
        tol = 0

    # 初始化W，W应该是n * n——neighbors维度，即n个样本有n个wi，每一个wi有n_neighbors， 这里做了转置
    W = np.zeros((n_neighbors, n))
    # 即1k，k维全为1的列向量
    I = np.ones((n_neighbors, 1))

    for i in range(n):
        # 对于每一个样本点xi
        # 先将xi进行伸展，形状同xj一致
        Xi = np.tile(data[i], (n_neighbors, 1)).T
        # xj所组成的矩阵
        Ni = data[N[i]].T
        # 求Yi
        Yi = np.dot((Xi-Ni).T, (Xi - Ni))
        # 这里是对于样本维度小于n_neighbors时做的特殊处理，MLLE算法，保持局部邻域关系的增量Hessian LLE算法
        Yi = Yi + np.eye(n_neighbors) * tol * np.trace(Yi)

        # 求解逆矩阵
        Yi_inv = np.linalg.pinv(Yi)
        # 求解每一个样本的wi，并做归一化处理
        wi = (np.dot(Yi_inv, I))/(np.dot(np.dot(I.T, Yi_inv), I)[0, 0])
        W[:, i] = wi[:, 0]

    # 初始化W
    W_y = np.zeros((n, n))

    # 对上一步求的W做进一步扩充，之前是n*k维的，现在变成n*n维的，不是近邻的位置补0
    for i in range(n):
        index = N[i]
        for j in range(n_neighbors):
            W_y[index[j], i] = W[j, i]


    I_y = np.eye(n)
    # 计算(I-W)(I-W).T
    M = np.dot((I_y - W_y), (I_y - W_y).T)
    # 求特征值
    eig_val, eig_vector = np.linalg.eig(M)
    # 找出前n_dim个小的特征值，忽略掉0，取第2到第n_dim+1个
    index_ = np.argsort(np.abs(eig_val))[1: n_dims+1]
    print("index_", index_)
    # 特征值对应的特征向量就是最后降维后得到的样本
    Y = eig_vector[:, index_]

    return Y

然后对上面的代码进行测试，首先导入一些必要的画图的工具包和数据集，数据集采用sklearn自带的“瑞士卷”数据集：

from sklearn.datasets import make_swiss_roll
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


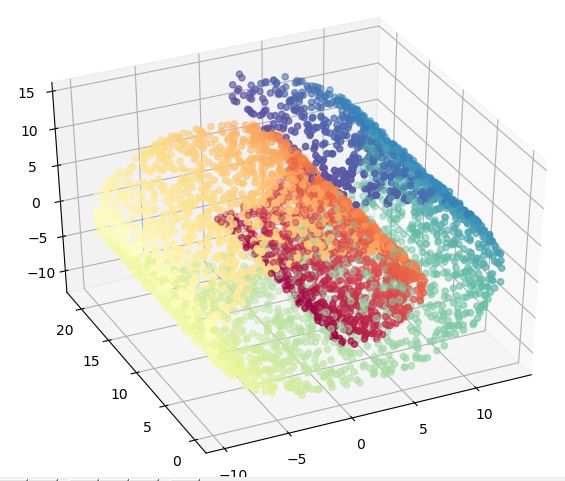
X, color = make_swiss_roll(n_samples=5000, noise=0.1, random_state=42)
fig = plt.figure()
ax = Axes3D(fig)
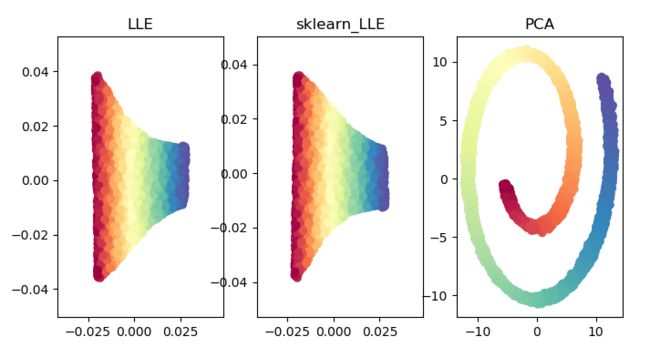
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=color, cmap=plt.cm.Spectral)

同时用sklearn自带的manifold方法实现LLE，并同时用PCA对上面的数据集进行降维，对比三者得到的结果：

from sklearn import manifold
from sklearn.decomposition import PCA


# LLE
data_1 = lle(X, n_neighbors=30)
# sklearn LLE
data_2 = manifold.LocallyLinearEmbedding(n_components=2, n_neighbors=30).fit_transform(X)
# PCA
pca_data = PCA(n_components=2).fit_transform(X)

# 画图
plt.figure(figsize=(8, 4))
plt.subplot(131)
plt.title("LLE")
plt.scatter(data_1[:, 0], data_1[:, 1], c=color, cmap=plt.cm.Spectral)

plt.subplot(132)
plt.title("sklearn_LLE")
plt.scatter(data_2[:, 0], data_2[:, 1], c=color, cmap=plt.cm.Spectral)


plt.subplot(133)
plt.scatter(pca_data[:, 0], pca_data[:, 1], c=color, cmap=plt.cm.Spectral)
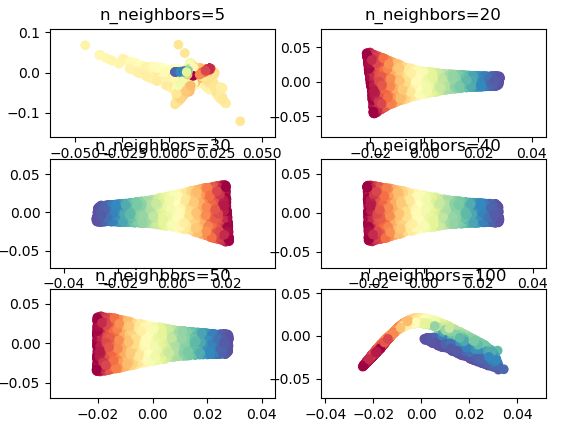
plt.title('PCA')

LLE算法对于所选取的局部样本点的个数较为敏感，所选取局部样本数量不同，对结果影响比较大，如下一组实验：

fig = plt.figure()
for index, k in enumerate((10, 20, 30, 40)):
    plt.subplot(2, 2, index+1)
    trans_data = manifold.LocallyLinearEmbedding(n_neighbors=k, n_components=2).fit_transform(X)
    plt.scatter(trans_data[:, 0], trans_data[:, 1], c=color, cmap=plt.cm.Spectral)

可以看出，当n_neighbors不同取值，对于结果的影响较大，当过多或者过少时，结果则会完全坏掉。

1.4 LLE的优缺点

LLE的原理大致就是上面所介绍的，那么在最后的实验中也比较了不同的近邻数目对结果的影响，在这里总结一些LLE的优点和缺点进行比较：

优点：

• • 方法简单易于实现，相较于ISOMAP而言，计算复杂度低；
  • LLE不同于PCA的线性降维，LLE是一种非线性的降维方法，能够学习任意维的流形图形；
  • 因为其非线性的特点，LLE能够表达局部特征，从而保留原数据特征。

当然，LLE也自身存在一些缺点：

• • 对于近邻算法选取的近邻样本点和样本点的数量较为敏感；
  • 仅能够学习流形图形，对于闭合的非流行图形，算法不适用；
  • LLE只能够用于稠密分布均匀的样本分布，稀疏的样本使用LLE算法效果不佳（这可能也是因为LLE对于近邻样本敏感所造成的）。

2 TSNE算法

前面介绍了两种降维的方法PCA和LLE，这两种降维的方法都有一个共同的特点：在进行降维时，都强调了降维后的相似的数据要尽可能地保持相似，但并没有说对于那些不相似的数据，要有多不相似这个问题，

这就导致了在进行降维时，可能导致数据的重叠问题，导致在低维空间中一样很难进行区分。

这时就需要另一种降维的方法——T-SNE。

所谓T-SNE，其就是SNE（stochastic neighbor embedding）的升级版，SNE同前面的算法一样，希望样本在高维空间中相似的数据点，到低维空间也相似，而T-SNE则是在SNE的基础上，要使得对于高维空间不相似的样本，在低维空间中也尽可能不相似。

SNE则把这种距离的关系转换为一种概率。下面先介绍二者共同的部分，对于区别和改进，在后边进行对比。这里仅做简要原理介绍，不再做过多推导。

首先，定义在高维空间中两个样本xⁱ和x^j之间的相似度S(xⁱ,x^j)，则：

这个概率表示，xⁱ作为中心点，x^j是其近邻点的概率，当两个点越近，则概率越大，距离较远时，则概率较小。

同样的，样本映射到低维空间后，分别为zⁱ和z^j，在低位空间中，二者的相似度定义为S'(zⁱ,z^j)，则：

然后根据这两个分布，在高维空间和低维空间中，我们希望这两个分布越相似越好，而用来衡量样本相似度的指标为KL散度，因此定义损失如下：

具体的KL散度的公式如下：

然后根据这个损失函数，找一组zⁱ和z^j，使得损失越小越好。然后就是梯度下降进行求解。

上面就是SNE与TSNE所共同的过程，在高维空间中，二者都采用高斯分布来度量任意两个点相似性，即：

而在低维空间中，SNE同样采用高斯分布作为相似性度量的方式，即：

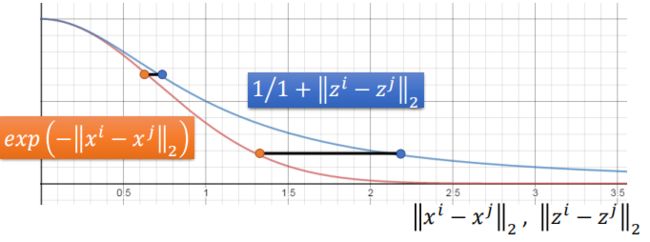
而对于TSNE来说，则采用了更一般的T分布来替代高斯分布：

这样可以不但拉近相似的样本的之间距离，同时，当样本不相似时，则可以使距离拉的更远。如下图所示：

对于两条曲线而言，当i与j相距较近时，二者在相似度上差不多，而当i与j相距较远时，T分布则可以进一步拉远二者之间的距离。

上面就是TSNE的基本思想，具体原理和算法这里不再进行推导，详细内容可以参考博客：TSNE-原理与实现。

关于TSNE的具体实现方法，git地址https://github.com/heucoder/dimensionality_reduction_alo_codes/tree/master/codes/T-SNE。这里就利用sklearn中的tsne方法对其进行实现和比较：

from sklearn.manifold import TSNE

plt.figure()
for index, k in enumerate((5, 15, 25, 30, 40, 100)):
    plt.subplot(230+index+1)
    data_tsne = TSNE(n_components=2, perplexity=k).fit_transform(X)
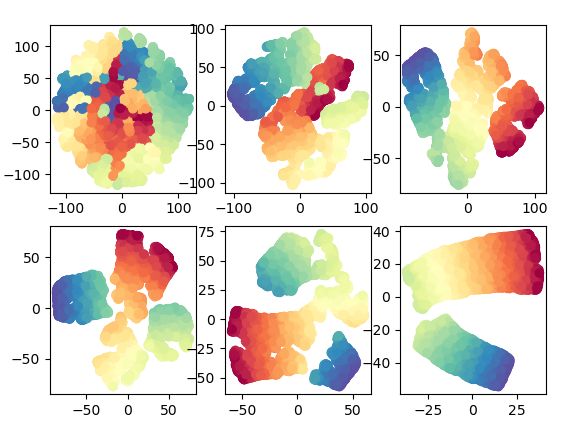
    plt.scatter(data_tsne[:, 0], data_tsne[:, 1], c=color, cmap=plt.cm.Spectral)

对于在手写数字识别上使用TSNE得到的结果，能够更加明显地看出TSNE的优点：

可以看出，TSNE解决了数据在降维之后的拥挤问题。

以上就是关于LLE和TSNE的内容，这里暂时没有对TSNE进行推导，后面自己会对TSNE的源代码进行熟悉和了解加深理解，本节有关降维的方法就先到这里了。

本文参考资料：

局部线性嵌入(LLE)原理总结

LLE原理及推导过程

李宏毅《机器学习》

---

降维的方法其实有很多，也有同一种的不同变形，当用到时后面会再进行补充。下一更准备对比较重要的算法AutoEnder做一个复习。