强化学习之policy-based方法A2C实现（PyTorch）
A2C：Advantage Actor Critic算法
policy gradient结合MC的思想就是REFORCEMENT算法，采用回合更新策略网络。如果对这个感兴趣的，可以看我的另一篇https://blog.csdn.net/MR_kdcon/article/details/111767945。
REFORCEMENT缺陷就是：
①：效率低，回合更新制。
②：直接用累计奖励做critic，其方差较大，收敛过程不稳定，可以通过对奖励做nomalization来缓解回合间相同状态的方差。
针对这两点，actor critic算法就诞生了，其用policy gradient结合TD的思想，采用步进更新策略网络。
一、Actor Critic算法
1.1、A2C算法简介
1.2、A2C算法伪代码
1.1、A2C算法简介
根据critic的不同，大致可将Actor critic分为A2C(Advantage actor critic)、A3C(Asynchronous advantage actor critic)、QAC(Q Advantage actor critic)三类。
如上图所示，在做policy gradient的时候，就算以衰减G为critic，其方差大问题还是存在，造成了收敛的不稳定性，因此我们需要将这个critic换成其期望的形式，即E(G),这样可以抑制方差大带来的不稳定。
看到E(G)，首先想到的就是value-based方法中的Q值函数，没错这里我们就是用Q值来取代G，至于后面的b，即baseline我们可以用V值函数来替代。
这样的话，优势函数Advantage function就变成了Q-V，而V是Q的期望值，故Q-V也是有正负的，这也符合我们设计baseline的初衷。
但是这样也存在一个小问题，除了策略网络以外，你还需要设计2个网络：即Q网络和V网络，为了简化成一个网络，可以对Q做个变式：
回忆一下贝尔曼等式
，这里可以进一步简化，根据期望公式，可转换成：
，虽然都说贝尔曼等式在有模型下才能用，但是上述这个等式在推导过程中可以约去转移概率P，故可以成立。
因此我们的优势函数就变成了
，这样我们设计一个网络就可以了，关键就是我们竟然推导出了TD error的V函数形式，这就可以和我们的DQN结合在一起了。
整个Actor critic算法结构如下：
最后你会发现，其实就是用TD error代替了G，其实V也可以充当TD目标值。只不过我们当初选择Q是因为，一是Q能选择动作而V不能；第二是因为当初用V做的时候，经过预测和控制之后，V仍需要转成Q，有了贝尔曼公式就很方便，然后用贪心策略从Q中选出了动作，那么model-free没有贝尔曼公式中的转移概率P，故为了省去这一步，我们直接选择了Q。但是现在动作有policy网络输出，故我们可以不用Q了。其实Q和V从定义就可以看出没啥大差别，就相差了个动作而已，都表达了未来价值的期望值。
上图是网络结构图，和Dueling网络一样之后，由共享网络和子网络组成，子网络分别为策略网络和V估计网络
1.2、算法伪代码
A2C算法流程：
评估点基于TD误差，Critic使用nn来计算TD误差并更新网络参数，Actor使用nn利用PG的更新方式来更新参数。
上述AC算法已经是一个很好的框架，但实际应用还较远。
二、A2C算法实战
2.1、环境介绍
2.2、算法解析
2.3、实验结果
2.1、环境介绍：
Pendulum：连续动作的RL环境。
目的：让杆子保持直立。
有关Pendulum环境的细节：https://github.com/openai/gym/wiki/Pendulum-v0
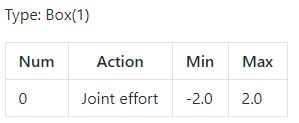
①：状态空间：Box(3)
②：动作空间：Box(1)，连续空间需要注意动作的2个区间值
Note：输入给环境的动作必须是个1维的向量。比如np.array([0.1])，而不能是0维的np.array(0.1)。
③：奖励：
最小-(pi^2 + 0.1*8^2 + 0.001*2^2) = -16.2736044
最大0
可以通过除以最小来归一化，增加收敛的稳定性。
④：初始位置
随机在[-π，π]的角度，[-1,1]的速度中采样。
⑤：终止状态
满200步
2.2、算法解析：
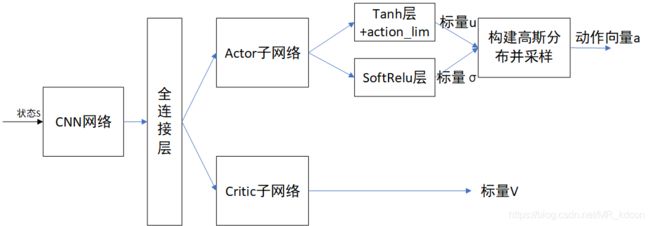
①：初始状态输入actor网络，网络的输出神经元为1个，分别产生一个均值u和标准差σ，用这两个值构建一个高斯分布，也就是说，高斯分布的均值和方差都由神经网络来近似。然后从中采样，将采样到的横坐标值通过裁减输出最后action。
②：action和环境交互，产生s_，r，将s、s_分别输入critic网络，网络的输出为V，故输出神经元也是1，产生V(s)，V(s_)。计算TD误差，一路进行backward更新值函数网络。
③：另一路与action对应的概率密度f取对数后相乘，别忘记Pytorch是基于minimize的，只有梯度下降，故还要取负号，最后backward更新actor网络参数。
④：这样一个step就完成了，然后s=s_，循环①②③④，直到200个step到来，才算一个epsiode完成。
tips：这里将与环境交互得到的r除以其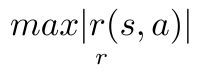
值，用于归一化，由于奖励实时奖励r(s,a)的方差比较大，类似于取期望、nomalization，归一化也有利于收敛的稳定性，让参数更新的幅度不要太大。
Note：在A2C中，并没有Experience Reply，其更新是利用相邻数据做单样本的随机梯度下降实现的。
下图是实际的共享网络，当然你也可以将Actor和Critic完全分开来也行：
2.3、实验结果：
训练1000个episode，然后统计每个episode获得的reward
这张图是未经训练下pendulum的结果。奖励值在[-90,-180]之间。
上面两张图是A2C算法的结果：训练虽然没有收敛，但还是有效果的，在直立的时候，奖励在0附近，而上面的结果有出现些许的接近0的值。
下面是测试过程，显然A2C本身的问题将造成难以收敛：
三、展望与总结
从上面实验可以看出，A2C算法在连续动作的RL上确有效果，但是总的来说A2C很难收敛。因为Critic很难收敛，其一是因为nn的输入要求独立同分布，即输入无关性，不连续，但A2C中critic网络，我们每次都拿下个状态的TD目标值和当前状态的V做loss，然后去更新参数，这种强相关性会让nn学不到东西，可以通过引入经验回放池打破相关性。其二是critic中TD目标值和V估计值公用一个网络，这其实就是NIPS DQN所犯的错误，这会让两者难以靠近，可以通过引入Target网络解决。critic网络这么难收敛，那么actor网络就更难收敛了。
总结：actor-critic提供了很好的框架，并且其采样步进更新，效率比REFORCEMENT更高，采用优势函数做critic，方差更小，稳定性更强，但收敛问题还有待提高，需要在此框架上继续修改。
提升方向：DDPG、A3C