OpenCV修养(三)——图像处理(上)
致谢
OpenCV高斯滤波GaussianBlur_godadream的博客-CSDN博客_gaussianblur
3 图像处理(一)
3.1 几何变换
3.1.1 图像缩放
cv2.resize(src,dsize,fx=0,fy=0,interpolation = cv2.INTER_LINEAR)
参数:
- src:输入图像
- dsize:按固定比例缩小
- fx、fy:自定义比例缩小
- interpolation:插值方法
插值 含义 cv2.INTER_LINEAR 双线性插值法 cv2.INTER_NEAREST 最近邻插值 cv2.INTER_AREA 像素区域重采样 cv2.INTER_CUBIC 双三次插值
import cv2 as cv
# 读取图片
img = cv.imread(r"C:\Users\13966\Desktop\Test01.jpg")
# 缩放
row, col = img.shape[0:2]
resize_img = cv.resize(img, (2*col, 2*row), cv2.INTER_NEAREST)
cv.imshow("image", resize_img)
cv.waitKey(0)
3.1.2 图像平移
cv.warpAffine(src,M,dsize)
- src:输入的图像
- M:2×3的
移动矩阵【这里移动矩阵我也是第一次听说,我后面去学学填上这个坑】- dsize:输出图像的大小
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family']='SimHei'
# 读取图像
img = cv.imread(r"C:\Users\13966\Desktop\Test01.jpg")
# 设置平移矩阵
rows, cols = img.shape[:2]
M = np.float32([[1, 0, 100], [0, 1, 50]])
dst = cv.warpAffine(img, M, (cols, rows))
# 图像显示
fig, axes = plt.subplots(nrows=1, ncols=2, figsize=(10, 8), dpi=100)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("原图")
axes[1].imshow(dst[:, :, ::-1])
axes[1].set_title("平移后结果")
plt.show()
out:
3.1.3 图像旋转
图像旋转是指图像按照某个位置转动一定角度的过程,旋转中图像仍然保持原始尺寸。
这里暂时埋坑!
3.1.4 仿射变换
图像的仿射变换设计到图像的形状位置角度的变化,是深度学习预处理中常用到的一个功能。仿射变换的主要工作是对图像进行缩放、旋转、翻转、平移等。
仿射变换的内核是两个点:
- 变换前是直线的,变换后依然是直线
- 直线比例保持不变
这里暂时埋坑!
3.2 图像阈值
ret,dst = cv2.threshold(src,thresh,maxval,type)
- src:输入图,只能输入单通道图像,通常来说为灰度图
- dst:输出图
- thresh:阈值
- maxval:当像素值超过了阈值,所赋予的值
- type:二值化操作的类型
- cv2.THRESH_BINARY:超过阈值部分取maxval,否则取0
- cv2.THRESH_BINARY_INV:THRESH_BINARY的反转
- cv2.THRESH_TRUNC:大于阈值部分设为阈值,否则不变
- cv2.THRESH_TOZERO:大于阈值部分不改变,否则设为0
- cv2.THRESH_TOZERO_INV:cv2.THRESH_TOZERO的反转
import cv2
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
img = cv.imread(r"C:\Users\13966\Desktop\Test01.jpg")
ret, thresh1 = cv2.threshold(img, 127, 255, cv.THRESH_BINARY)
ret, thresh2 = cv2.threshold(img, 127, 255, cv.THRESH_BINARY_INV)
ret, thresh3 = cv2.threshold(img, 127, 255, cv.THRESH_TRUNC)
ret, thresh4 = cv2.threshold(img, 127, 255, cv.THRESH_TOZERO)
ret, thresh5 = cv2.threshold(img, 127, 255, cv.THRESH_TOZERO_INV)
title = ['img', 'THRESH_BINARY', 'THRESH_BINARY_INV', 'THRESH_TRUNC',
'THRESH_TOZERO', 'THRESH_TOZERO_INV']
fig, axes = plt.subplots(nrows=2, ncols=3, figsize=(20, 8), dpi=80)
axes[0][0].imshow(img[:, :, ::-1])
axes[0][0].set_title(title[0])
axes[0][1].imshow(thresh1[:, :, ::-1])
axes[0][1].set_title(title[1])
axes[0][2].imshow(thresh2[:, :, ::-1])
axes[0][2].set_title(title[2])
axes[1][0].imshow(thresh3[:, :, ::-1])
axes[1][0].set_title(title[3])
axes[1][1].imshow(thresh4[:, :, ::-1])
axes[1][1].set_title(title[4])
axes[1][2].imshow(thresh5[:, :, ::-1])
axes[1][2].set_title(title[5])
plt.show()
out:
3.3 图像平滑
3.3.1 图像噪声
由于图像采集、处理、传输等过程不可避免的会受到噪声的污染,妨碍人们对图像理解及分析处理,常见的噪声有高斯噪声、椒盐噪声等。
3.3.1.1 椒盐噪声
椒盐噪声也称为脉冲噪声,是图像中经常见到的一种噪声,它是一种随机出现的白点或者黑点,其出现的原因可能是因为影像讯号受到突如其来的强烈干扰而产生。如下图所示:
3.3.1.2 高斯噪声
高斯噪声满足高斯分布。
3.3.2 均值滤波
均值滤波实际上就是深度学习里面的平均池化。
让我们先给出一张带有噪点的图片,以便下面做处理。
我们来解释一下池化的含义。
池化是卷积神经网络CNN的术语。认识什么是池化之前,我们要先了解什么是卷积,卷积就是通过一个小型矩阵(卷积核)对原图片矩阵做扫描来输入另外一个矩阵,这个另外的矩阵我们叫做卷积层。
小型矩阵和原图片矩阵的映射关系是通过互相关运算来实现的,即对应的元素相乘在相加。如下图所示:
理解了原理就好说了。池化层也是通过某种关系来输出新矩阵的,根据这种关系我们将池化层分为平均池化层和最大池化层,其本质是用一个n×n的卷积核去扫描,而这个卷积核是没有数字的,且他也不和原图片做互相关运算。如果是平均池化层,那么是输出卷积核覆盖区域的平均数;而如果是最大池化层,则输出卷积核覆盖区域的最大数。
举个例子,用2×2的池化窗口去扫描,如果窗口内的值是
-
max(0,1,3,4)=4,
-
max(1,2,4,5)=5,
-
max(3,4,6,7)=7,
-
max(4,5,7,8)=8。
说完了池化,让我们回到滤波器。实际上,均值滤波的本质实际上就是平均池化窗口。
让我们试着对上面的图片做一下均值滤波处理。
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test03.jpg")
blur_img = cv.blur(img, (3, 3))
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(blur_img[:, :, ::-1])
axes[1].set_title("blur_img")
plt.show()
out:
3.3.3 方框滤波
cv2.boxFilter( src, ddepth, ksize, anchor, normalize, borderType)
- src指的是处理的图像
- ddepth:处理结果图像的图像深度,一般使用1 表示与原始图像使用相同的图像深度
- normalize:是否进行归一化
方框滤波使用归一化时效果和均值滤波完全一样,而不使用归一化时,超过255的像素点默认会变成255,,如下所示。
import cv2 as cv
import matplotlib.pyplot as plt
img = cv.imread(r"C:\Users\13966\Desktop\Test03.jpg")
blur_img = cv.boxFilter(img, -1, (3, 3), normalize=False)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(blur_img[:, :, ::-1])
axes[1].set_title("blur_img")
plt.show()
out:
3.3.4 高斯滤波
cv2.GaussianBlur(src, ksize, sigmaX, sigmaY=0, borderType=BORDER_DEFAULT);
src:输入图像
ksize:高斯卷积核的大小
sigmaX:表示水平方向的标准差
sigmaY:表示垂直方向的标准差,默认为0,表示于sigmaX相同
- borderType:边缘填充类型,默认无填充
高斯滤波器(卷积核)里的数值满足高斯分布。
高斯滤波是一种线性平滑滤波,适用于消除高斯噪声,广泛应用于图像处理的减噪过程。通俗的讲,高斯滤波就是对整幅图像进行加权平均的过程,每一个像素点的值,都由其本身和领域内的其他像素值经过加权平均后得到。
import cv2 as cv
import matplotlib.pyplot as plt
img = cv.imread(r"C:\Users\13966\Desktop\Test03.jpg")
blur_img = cv.GaussianBlur(img, (3, 3), 1)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(blur_img[:, :, ::-1])
axes[1].set_title("blur_img")
plt.show()
out:
3.3.5 中值滤波
中值滤波是效果最好的滤波器,它是这么做的。用一个n×n(n一般为奇数)的卷积核去扫描一副图像,在卷积核每一次覆盖到的位置中,将里面所有的数字从小到大排列后取中位数,用中位数替换卷积核所在位置的中间值。如下图所示:
import cv2 as cv
import matplotlib.pyplot as plt
img = cv.imread(r"C:\Users\13966\Desktop\Test03.jpg")
blur_img = cv.medianBlur(img, 5)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(blur_img[:, :, ::-1])
axes[1].set_title("blur_img")
plt.show()
out:
3.3.6 小结
图像处理中,常用的滤波算法有均值滤波、中值滤波以及高斯滤波等。
两种噪声:
| 噪声 | 说明 |
|---|---|
| 椒盐噪声 | 图像中随机出现的白点或者黑点 |
| 高斯噪声 | 噪声的概率分布是正态分布 |
三种滤波器的对比:
| 滤波器种类 | 基本原理 | 特点 |
|---|---|---|
| 均值滤波 | 使用模板内所有像素的平均值代替模板中心像素灰度值 | 算法简单计算速度快,易收到噪声的干扰,不能完全消除噪声,只能相对减弱噪声 |
| 中值滤波 | 计算模板内所有像素中的中值,并用所计算出来的中值体改模板中心像素的灰度值 | 对噪声不是那么敏感,能够较好的消除椒盐噪声,但是容易导致图像的不连续性 |
| 高斯滤波 | 对图像邻域内像素进行平滑时,邻域内不同位置的像素被赋予不同的权值 | 对图像进行平滑的同时,同时能够更多的保留图像的总体灰度分布特征,对于高斯噪声处理效果很好 |
我不是很建议你在初次学习的时候深究这些滤波器背后的数学原理,因为对于数学基础不好的人来说一旦陷进去对自己的打击很大。
3.4 形态学操作
形态学转换是基于图像形状的一些简单操作,它通常在二进制图像上执行。腐蚀和膨胀是两个基本的形态学运算符,他也有一些变体形式,如开运算、闭运算、礼帽黑帽等。
3.4.1 连通性
3.4.1.1 邻接
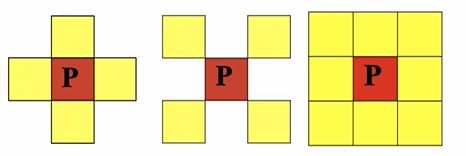
在图像中,最小的单位是像素,每个像素周围有8个邻接像素。常见的邻接关系有3种:4邻接、8邻接和D邻接。
其中我们用 N 4 ( p ) N_4(p) N4(p)表示像素p的4邻接,同理 N D ( p ) N_D(p) ND(p), N 8 ( p ) N_8(p) N8(p)。
3.4.1.2 连通
连通性是描述区域和边界的重要概念,两个像素连通的两个必要条件是:
- 两个像素的位置是否相邻
- 两个像素的灰度值是否满足特定的相似性准则
连通也分三种,即4连通、8连通和m连通。
- 4连通:对于具有值V的像素p和q,如果q在集合 N 4 ( p ) N_4(p) N4(p)中,则称这两个像素是4连通。
- 8连通:对于具有值V的像素p和q,如果q在集合 N 8 ( p ) N_8(p) N8(p)中,则称这两个像素是8连通。
- m连通:m连通就是同时满足4连通和D连通即为m连通。
3.4.2 腐蚀和膨胀
腐蚀和膨胀是最基本的形态学操作,其都是针对白色部分而言。换而言之就是对高亮区域的扩大与缩小。
3.4.2.1 腐蚀
腐蚀的具体操作是用一个结构元素扫描图像中的每一个元素,用结构元素中的每一个元素与其覆盖的像素做“与”操作,如果都为1,则该像素为1,否则为0。如下图所示,结构A被结构B(我们暂且看做是卷积核)腐蚀后:
腐蚀的作用就是消除物体边界点,使目标缩小,其可以消除小于结构元素的噪声点。通俗来说就是让白色部分变小。
cv.erode(src,kernel,iterations,borderType,bordervalue)
- src:要处理的图像
- kernel:核结构
- iterations:腐蚀次数,默认为1
- borderType:填充类型
- bordervalue:填充值
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test03.jpg")
kernel = np.ones((5, 5))
new_img = cv.erode(img, kernel)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
out:
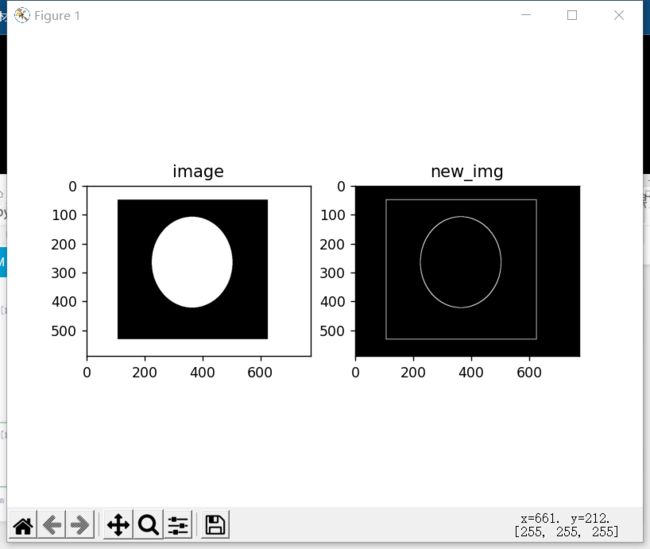
3.4.2.2 膨胀
膨胀的具体操作是用一个结构元素扫描图像中的每一个元素,用结构元素中的每一个元素与其覆盖的像素做“与”操作,如果都为0,则该像素为0,否则为1。其原理和腐蚀很像的,我就不画图了,太累了。通俗来讲,膨胀实际上就是扩大白色部分。
cv.dilate(src,kernel,iterations,borderType,bordervalue)
- src:要处理的图像
- kernel:核结构
- iterations:腐蚀次数,默认为1
- borderType:填充类型
- bordervalue:填充值
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test03.jpg")
kernel = np.ones((5, 5))
new_img = cv.dilate(img, kernel)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
out:
3.4.3 开闭运算
开运算和闭运算和按照一定的次序去进行腐蚀和膨胀,但将原图开运算后是无法通过闭运算返回原图的。
开运算是先腐蚀后膨胀,其作用是分离物体,消除小区域。说成人话就是,如果你的图像是全是黑的,但是其中有一些白色的噪声点,那么开运算可以使你的图片先去除白色噪声,然后又恢复原来的图片,这实际上是一个去除毛刺的操作;闭运算是先膨胀后腐蚀,其作用是消除/闭合物体里面的孔洞,可以填充闭合区域。说成人话就是,先膨胀让白色噪声变大,后腐蚀白色噪声就无法消除了,所以所得图片应该是和原图差不多的白色噪声或比原图还大的白色噪声。说了我们也听不太懂,我们试着来处理一下。
cv.morphologyEx(src,op,kernel)
- src:要处理的图像
- op:处理的方式,进行开运算则cv.MORPH_OPEN,若进行闭运算,则设为cv.MORPH_CLOSE
- Kernel:核结构
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test01.jpg")
kernel = np.ones((3, 3))
new_img = cv.morphologyEx(img, cv.MORPH_OPEN, kernel)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
有没有感觉,这车子有点快跑出来的感觉。
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test01.jpg")
kernel = np.ones((3, 3))
new_img = cv.morphologyEx(img, cv.MORPH_CLOSE, kernel)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
3.4.4 黑帽和礼帽
礼帽运算实际上是原图像和开运算结果之差。
试想,开运算实际上就是消除白色毛刺,而原图像又带有刺,你用带有刺的减去没带刺的,得到的结果(礼帽)不就是只有刺的图了吗。
开运算虽然优化了图片,但是放大了裂缝或者局部低亮度的区域,因此,从原图中减去开运算后的图,得到的效果图突出了比原图轮廓周围的区域更明亮的区域,且这一操作和选择的核的大小有关。
而黑帽运算实际上是闭运算和原图像之差。简单来说,闭运算使得噪声变大或不变,减去原图像,得到的就是噪声的轮廓。
黑帽运算后的效果图突出了比原图轮廓周围的区域更暗的区域,且这一操作和选择的核的大小有关。
黑帽运算用来分离比邻近点暗一些的斑块。
同样的,黑帽运算和礼帽运算使用的是与开闭运算一样的API。
cv.morphologyEx(src,op,kernel)
- op部分选择MORPH_TOPHAT则为礼帽,选择MORPH_BLACKHAT则为黑帽
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test01.jpg")
kernel = np.ones((3, 3))
#new_img = cv.morphologyEx(img, cv.MORPH_TOPHAT, kernel)
new_img = cv.morphologyEx(img, cv.MORPH_BLACKHAT, kernel)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
out:
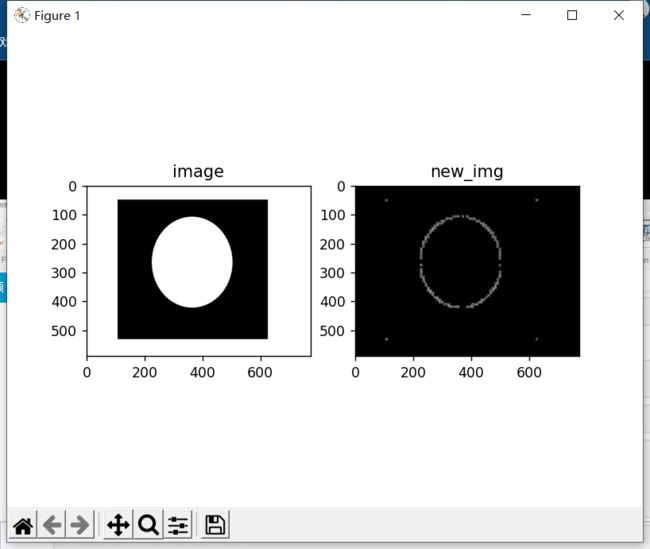
3.4.5 梯度
做一个梯度运算实际上就是先膨胀,再拿原图膨胀的结果减去原图腐蚀的结果。膨胀扩大白色区域,腐蚀缩小白色区域,两个一做差,那么得到的肯定是白色区域的轮廓。如下图所示:
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test04.jpg")
kernel = np.ones((3, 3))
new_img = cv.morphologyEx(img, cv.MORPH_GRADIENT, kernel)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
3.5 图像梯度处理
3.5.1 Sobel算子
如上图,我们如果在图中画一根红线,红线的左右有梯度吗?明显地,这里我们讲的梯度可以用一个更简单的词来代替,即色差。可以看出,这条红线左右是不存在梯度的。
那我们不禁想问,哪里有梯度呢?当然是这个白圈的边缘了。
在形态学操作中,我们似乎都是用一个核去扫描图像,在这里我们同样这么做。我们可以用以下的卷积核去检测区域的左右边缘。
G x = [ − 1 0 + 1 − 2 0 + 2 − 1 0 + 1 ] ∗ A G_x = \left[\begin{array}{cc}-1&0&+1\\ -2&0&+2\\ -1&0&+1\end{array}\right]*A Gx=⎣⎡−1−2−1000+1+2+1⎦⎤∗A
我们可以用以下的卷积核去检测区域的上下边缘。
G y = [ − 1 − 2 − 1 0 0 0 + 1 + 2 + 1 ] ∗ A G_y = \left[\begin{array}{cc}-1&-2&-1\\ 0&0&0\\ +1&+2&+1\end{array}\right]*A Gy=⎣⎡−10+1−20+2−10+1⎦⎤∗A
我们把以上两个卷积核叫做Sobel算子矩阵,其用于增强边缘的差异。当检测目标区域边缘时,我们可以用对应的核与目标区域做互相关运算。拿 G x G_x Gx来说,其计算的结果我们可以看成是0列左右的差异值,即看成是梯度。
说完原理,让我们看一下在OpenCV中如何使用Sobel算子。
dst = cv2.Sobel(src,ddepth,dx,dy,ksize)
- ddeph:图像深度
- dx和dy分别表示水平和竖直方向
- ksize是Sobel算子的大小
import cv2
import cv2 as cv
import matplotlib.pyplot as plt
img = cv.imread(r"C:\Users\13966\Desktop\Test04.jpg")
new_img = cv.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
out:
从指定参数和输出结果来看,由于在sobel中我们指定参数dy = 0,dx = 1,说明使用上述Sobel算子矩阵 G x G_x Gx。此矩阵右边为正左边为负。在图像中,看往左半边圆圈为白(255)方框为黑(0),则结果Sobel运算后得出结果为正数,所以得出的图像左半圈留白明显。其他情况也可按照上述推导过程推出结果,这里不过多赘述。
在Sobel运算中,白到黑是正数,黑到白是负数,而负数会被截断成0,所以通常我们要取绝对值。
import cv2
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test04.jpg")
# kernel = np.ones((3, 3))
new_img = cv.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
new_img = cv2.convertScaleAbs(new_img)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
out:
当你想要同时检测左右边缘和上下边缘时,同时对参数dx和dy设为1未尝不可,但是由于dx设为1时上下会黑,dy设为1时左右会黑,当同时开启时,可以会导致上下左右都会黑,而不会出现完美检测轮廓的效果。如下图所示:
import cv2
import cv2 as cv
import matplotlib.pyplot as plt
img = cv.imread(r"C:\Users\13966\Desktop\Test04.jpg")
new_img = cv.Sobel(img, cv2.CV_64F, 1, 1, ksize=3)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
out:
为此,我们可以分别求解 G x G_x Gx和 G y G_y Gy,然后将两者用图像混合操作按比例混合即可。如下所示:
import cv2
import cv2 as cv
import matplotlib.pyplot as plt
import numpy as np
img = cv.imread(r"C:\Users\13966\Desktop\Test04.jpg")
new_img_x = cv.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
new_img_y = cv.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
new_img = cv.addWeighted(new_img_x, 0.5, new_img_y, 0.5, 0)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("image")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("new_img")
plt.show()
out:
上面的图片似乎不是很能看出效果,我们用另外一张图片来看看效果:
import cv2
import cv2 as cv
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family']='SimHei'
img = cv.imread(r"C:\Users\13966\Desktop\Test02.jpg")
new_img = cv.Sobel(img, cv2.CV_64F, 1, 1, ksize=3)
new_img_x = cv.Sobel(img, cv2.CV_64F, 1, 0, ksize=3)
new_img_y = cv.Sobel(img, cv2.CV_64F, 0, 1, ksize=3)
new_img1 = cv.addWeighted(new_img_x, 0.5, new_img_y, 0.5, 0)
fig, axes = plt.subplots(nrows=1, ncols=3)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("原图")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("指定参数效果")
axes[2].imshow(new_img1[:, :, ::-1])
axes[2].set_title("混合效果")
plt.show()
out:
3.5.2 Scharr算子
Scharr算子与Sobel算子类似,只不过它对于边缘的检测效果会放大。
G x = [ − 3 0 3 − 10 0 10 − 3 0 3 ] ∗ A G_x = \left[\begin{array}{cc}-3&0&3\\ -10&0&10\\ -3&0&3\end{array}\right]*A Gx=⎣⎡−3−10−30003103⎦⎤∗A
G y = [ − 3 − 10 − 3 0 0 0 − 3 − 10 − 3 ] ∗ A G_y = \left[\begin{array}{cc}-3&-10&-3\\ 0&0&0\\ -3&-10&-3\end{array}\right]*A Gy=⎣⎡−30−3−100−10−30−3⎦⎤∗A
我们来看看它对于图片的处理效果:
import cv2
import cv2 as cv
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family'] = 'SimHei'
img = cv.imread(r"C:\Users\13966\Desktop\Test02.jpg")
new_img_x = cv.Scharr(img, cv2.CV_64F, 1, 0)
new_img_y = cv.Scharr(img, cv2.CV_64F, 0, 1)
new_img = cv.addWeighted(new_img_x, 0.5, new_img_y, 0.5, 0)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("原图")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("Scharr算子效果")
plt.show()
out:
3.5.3 laplacian算子
laplacian算子和上述两个算子不同,其由二阶导组成,对于一些边缘十分敏感,这虽然能够提高精度,但是却易受噪点影响。
G = [ 0 1 3 1 − 4 1 0 1 0 ] G = \left[\begin{array}{cc}0&1&3\\ 1&-4&1\\ 0&1&0\end{array}\right] G=⎣⎡0101−41310⎦⎤
对于拉普拉斯算子,其由于是二阶导,所以不必在添加dx和dy参数。如下所示:
import cv2
import cv2 as cv
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.family'] = 'SimHei'
img = cv.imread(r"C:\Users\13966\Desktop\Test02.jpg")
new_img = cv.Laplacian(img, cv2.CV_64F)
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].imshow(img[:, :, ::-1])
axes[0].set_title("原图")
axes[1].imshow(new_img[:, :, ::-1])
axes[1].set_title("拉普拉斯算子效果")
plt.show()
out: