一文教你搞懂2D卷积和3D卷积

前言

    本人最近在搞毕设时发现自己一直会搞混2D卷积和3D卷积，于是在网上查阅了大量资料，终于明白了其中的原理。希望刷到这篇博客的小伙伴能够停下来静心阅读10分钟，相信你读完之后一定会有所收获。

2D卷积

单通道卷积

    在深度学习中，卷积是最基本的乘法和加法，对于一幅只有一个信道的图像，其卷积如图所示（本例中stride = 1, padding = 0）。

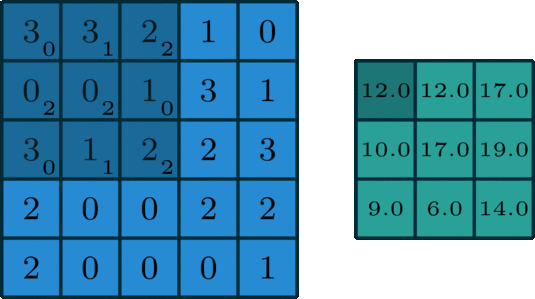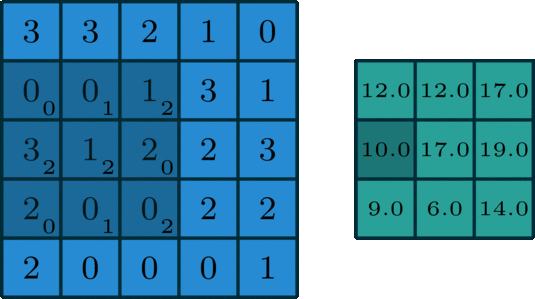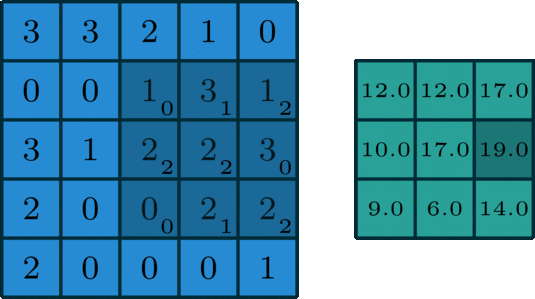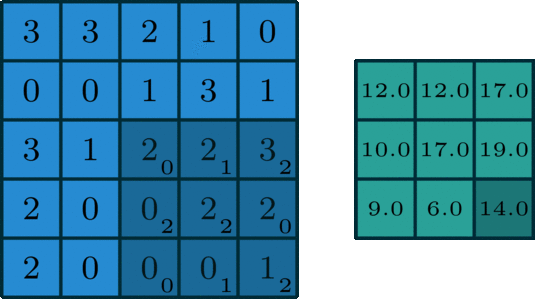
    这里的过滤器是一个3×3的矩阵，它的元素是[[0,1,2]，[2,2,0]，[0,1,2]]。过滤器在输入端滑动。在每个位置，它都在做元素的乘法和加法。每个滑动位置都以一个数字结束。最终的输出是一个3x3矩阵。

多通道卷积

    多通道卷积过程如下：每个kernel都应用于前一层的输入通道，以生成一个输出通道。我们对所有kernel重复这个过程以生成多个通道。然后将这些通道汇总在一起，形成一个单独的输出通道。
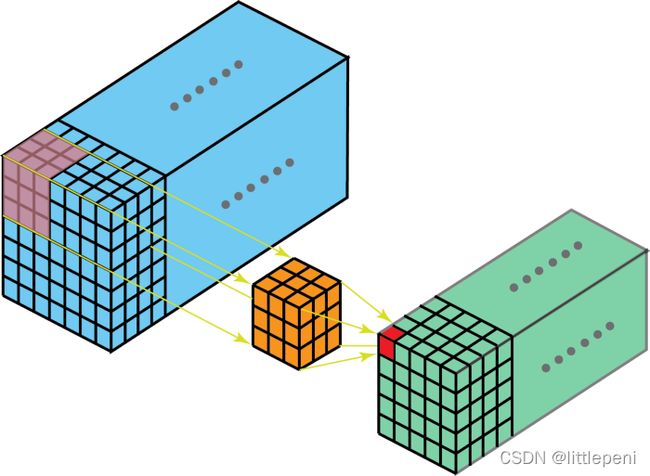
    这里的输入层是一个5×5×3的矩阵，有3个通道。Convolution Filter是一个3×3×3矩阵。首先，Filter中的每个kernel分别应用于输入层中的三个通道，执行三个卷积，得到3个通道，大小为3 x 3。

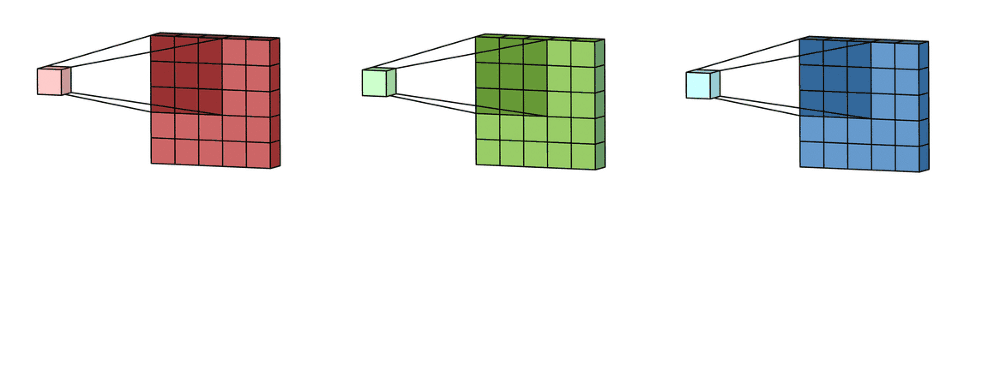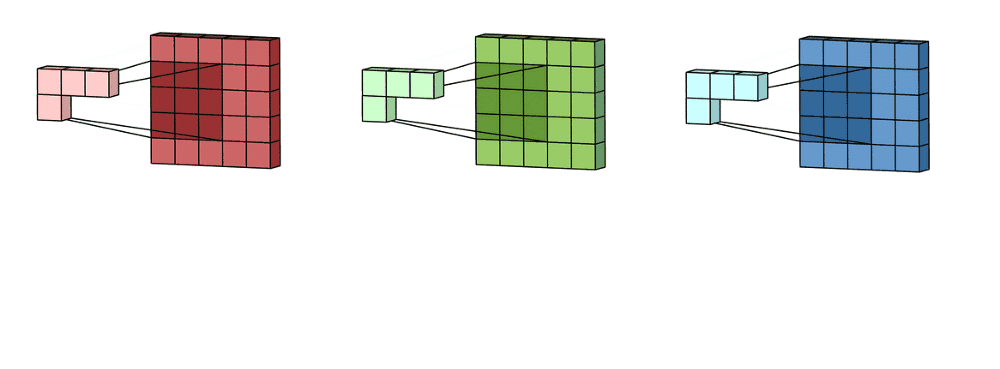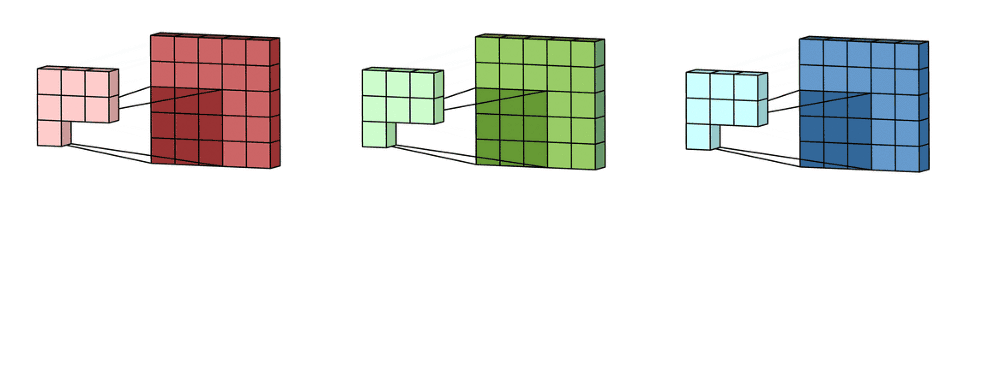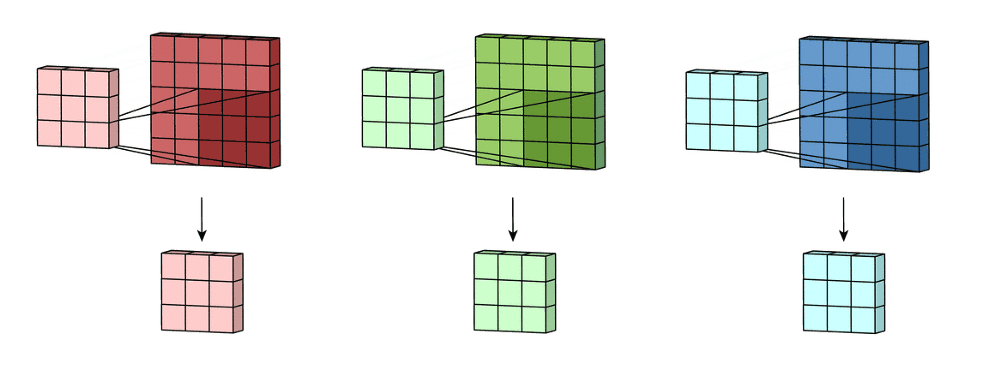
    在5×5矩阵上执行遍历的就是每一个kernel。然后这三个输出的通道相加(元素相加)形成一个单独的通道(3 x 3 x 1)。这个最终的单通道就是使用Filter(3 x 3 x 3矩阵)对输入层(5 x 5 x 3矩阵)进行卷积的结果。

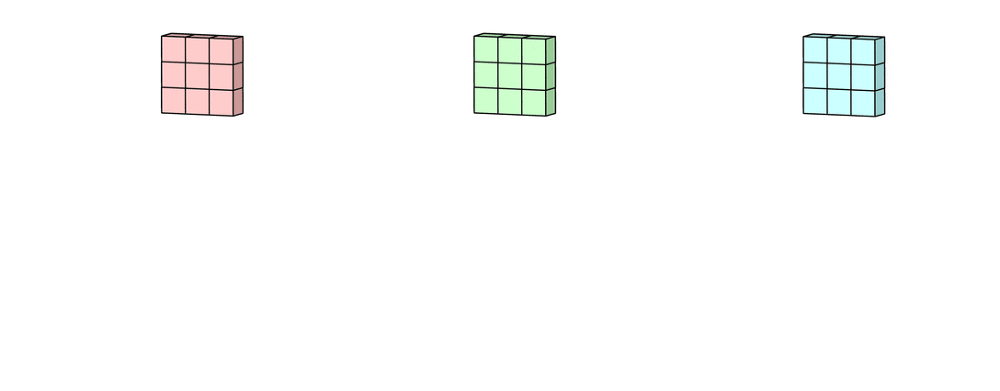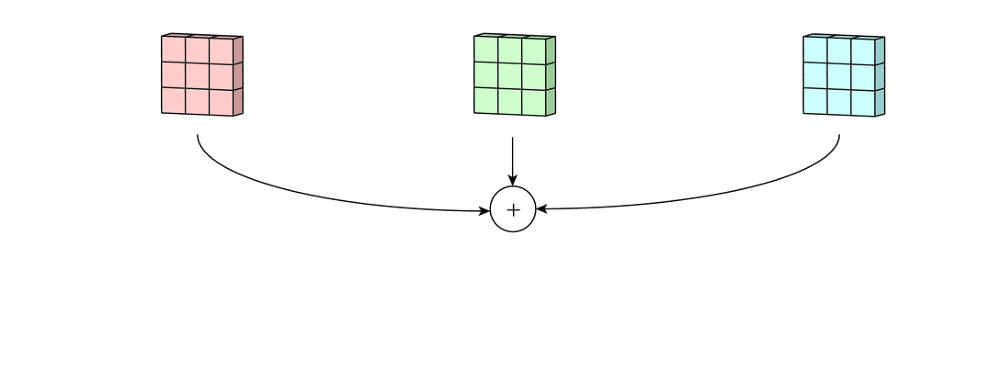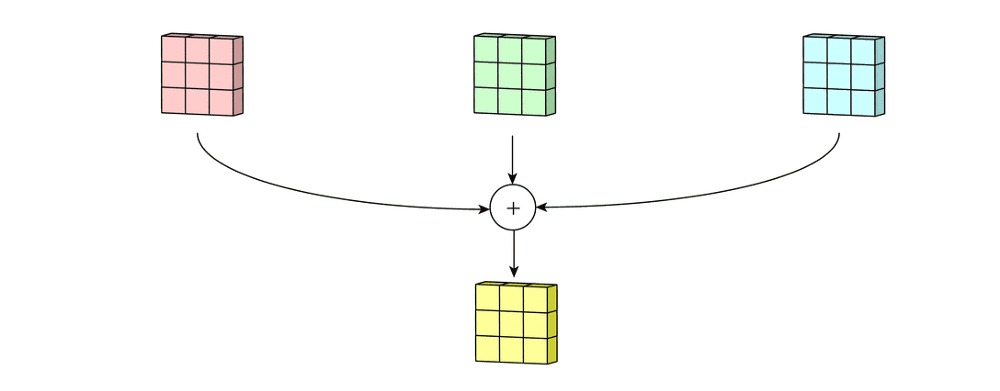
    我们可以认为此过程是将3D Filter矩阵滑过输入层。请注意，输入层的通道数和Filter的Kernel数相同。3D Filter 只能在图像的2个方向（高度和宽度）上移动（这就是为什么这种操作被称为2D卷积的原因，尽管3D Filter 用于处理3D体积（高度×宽度×通道数）数据）。在每个滑动位置，我们执行逐元素的乘法和加法运算，结果为单个数字。
  在以下示例中，滑动在水平5个位置和垂直5个位置（5=7-3+1)进行。在深度方向上再进行元素相加后，我们得到一个输出通道。

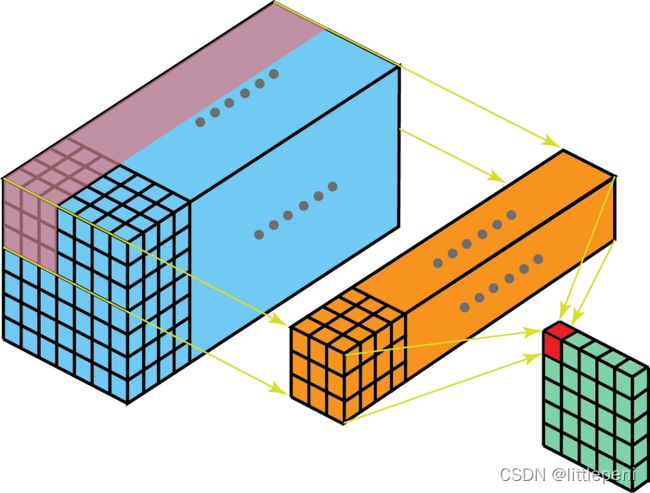
    现在我们可以知道如何在不同深度的图层之间进行变换。假设输入层具有Din通道，而我们希望输出层具有Dout通道。我们需要做的只是将Dout 个Filter应用于输入层，每个Filter都有Din个kernel，每个Filter提供一个输出通道。应用Dout个Filter后，我们将拥有Dout个通道，然后可以将它们堆叠在一起以形成输出层。（输出层的Dout个通道也可称为Dout个Feature map，因此输出的Feature map数实际与Convolution Filter的数量相同。）

3D卷积

    在上面已经解释过，虽然我们是在3D数据（高度×宽度×通道数）上进行卷积，但由于Convolution Filter只能在高度和宽度方向上移动，因此仍被称为2D卷积，一个Filter和一张图像卷积只能生成一个通道的输出数据。
    3D卷积使用的数据和2D卷积最大的不同就在于数据的时序性。3D卷积中的数据通常是视频的多个帧或者是一张医学图像的多个分割图像堆叠在一起，这样每帧图像之间就有时间或者空间上的联系。
    下面这张图可以说明3D卷积的大致过程。左边是输入层，此时我们在空间上看到的3维（即深度方向）不再表示通道数，而是图片的帧数，**也就是说这其实是图像中的单个通道的一帧帧图片堆叠之后的效果。**因此对于三通道（RGB）图像组成的一段视频，实际应该包含三个这样的3D数据，这里只是其中一个通道。Convolution Filter的深度不再与通道数相同（很显然），只需要满足<=帧数即输入层的深度即可。总结一下，输入层现在的维度是（Channel×Depth1×Height1×Width1），Filter的维度是（Depth2×Height2×Width2）。
    自然地，卷积核就可以在深度、高度、宽度三个方向上自由移动，两个立方体之间的每一层进行卷积然后再在深度上逐元素相加，得到一个数据，形成一个平面后，卷积核向深度方向移动，继续卷积，于是就输出了一个3D的Feature map。
    有人可能会问，一个通道的多个帧和一个Filter生成了一个3D Feature map，那三通道的图像卷积最后就一定生成三个3D Feature map吗，它们的转化关系究竟是怎么样的？？关于这里的疑惑，我们放到代码部分来讲解。先再次强调，输出层的通道数就等价于输出层的Feature map数！！

代码部分

    相信通过上面理论部分知识的讲解，小伙伴已经能看懂个大概了，接下来我们就用代码来证明一下。这里使用的是深度学习框架Pytorch。

2D Convolution

    首先创建一个模型：

import torch as t
import torch.nn as nn

class A(nn.Module):
    
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(2, 2, 3)
        self.conv2 = nn.Conv2d(2, 2, 3)
        self.conv3 = nn.Conv2d(2, 2, 3)
        
    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = self.conv3(x)
        
        return x

    这个模型非常的简单，就是三个2D卷积层的结构，每个卷积层的输入通道数和输出通道数均为2，卷积核的size是（3，3）。具体可以参照以下参数定义：

torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True, padding_mode='zeros', device=None, dtype=None)

    然后我们输出模型每一层的参数：

a=A()
print(list(a.parameters()))

    结果如下：

Parameter containing:
tensor([[[[-0.0299,  0.0891,  0.0303],
          [ 0.0869, -0.0230, -0.1760],
          [ 0.1408,  0.0348,  0.1795]],

         [[ 0.2001,  0.0023, -0.1775],
          [ 0.0947, -0.0231, -0.1756],
          [ 0.1201, -0.0997, -0.0303]]],


        [[[-0.0425,  0.0748, -0.1754],
          [-0.1191, -0.1203, -0.1219],
          [-0.0794,  0.0895, -0.1719]],

         [[ 0.1968, -0.0463,  0.0550],
          [-0.0386,  0.1594,  0.1282],
          [-0.0009,  0.2167, -0.1783]]]], requires_grad=True)
Parameter containing:
tensor([ 0.0147, -0.0406], requires_grad=True)
Parameter containing:
tensor([[[[-0.0578, -0.1114, -0.1194],
          [-0.1469, -0.1175, -0.1616],
          [-0.2289, -0.0975, -0.1700]],

         [[-0.0894,  0.0074,  0.1222],
          [-0.0176, -0.0509,  0.1622],
          [-0.0405, -0.1349,  0.1782]]],


        [[[-0.0739,  0.2167,  0.1864],
          [ 0.0956, -0.1761,  0.0464],
          [ 0.0062, -0.0685,  0.0748]],

         [[ 0.1085,  0.1481,  0.1334],
          [ 0.2236, -0.0706, -0.0224],
          [ 0.0079, -0.1835, -0.0407]]]], requires_grad=True)
Parameter containing:
tensor([-8.0720e-05,  1.6026e-01], requires_grad=True)
Parameter containing:
tensor([[[[-0.0702,  0.1846,  0.0419],
          [-0.1891, -0.0893, -0.0024],
          [-0.0349, -0.0213,  0.0936]],

         [[-0.1062,  0.1242,  0.0391],
          [-0.1924,  0.0535, -0.1480],
          [ 0.0400, -0.0487, -0.2317]]],


        [[[ 0.1202,  0.0961,  0.2336],
          [ 0.2225, -0.2294, -0.2283],
          [-0.0963, -0.0311, -0.2354]],

         [[ 0.0676, -0.0439, -0.0962],
          [-0.2316, -0.0639, -0.0671],
          [ 0.1737, -0.1169, -0.1751]]]], requires_grad=True)
Parameter containing:
tensor([-0.1939, -0.0959], requires_grad=True)

    接下来我们需要对这个输出结果进行详细分析了。可以看出输出的一共有6个Tensor，即每一个卷积层输出了2个Tensor。首先观察一维Tensor，这个是self.bias，加到输出层的每个通道上，因此只有两个元素。那么为什么卷积层的参数Tensor的维度是（2，2，3，3）呢？因为在nn.Conv2d(2, 2, 3)中可以看中输出channel数是2，因此有2个filter，每个filter的深度又和输入层的channel数相同，所以每个filter的kernel数为2，每个kernel的size又是（3，3），所以最终维度是（2，2，3，3）。 代码输出结果证明了理论的正确性。

3D Convlution

    同理，定义一个模型并输出每层参数：

import torch as t
import torch.nn as nn


class A(nn.Module):

    def __init__(self):
        super().__init__()
        # Conv3d的输入是5维的Tensor(N,C_in,D_in,H_in,W_in),输出为(N,C_out,D_out,H_out,W_out)
        self.conv1 = nn.Conv3d(
            1,  # 输入图像的channel数,C_in
            3,  # 卷积产生的channel数,C_out
            kernel_size=2,  # 卷积核的尺寸,这里实际是(2,2,2),第一维表示卷积核处理的帧数
            stride=(1,1,1),  # 卷积步长,(D,H,W)
            padding=(0,0,0),  # 输入的每一条边补充0的层数,(D,H,W)
            bias=False)
        self.conv2 = nn.Conv3d(
            1,  # 输入图像的channel数,C_in
            3,  # 卷积产生的channel数,C_out
            kernel_size=2,  # 卷积核的尺寸,这里实际是(2,2,2),第一维表示卷积核处理的帧数
            stride=(1, 1, 1),  # 卷积步长,(D,H,W)
            padding=(0, 0, 0),  # 输入的每一条边补充0的层数,(D,H,W)
            bias=False)

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)

        return x


if __name__ == "__main__":
    a=A()
    print(list(a.parameters()))

    结果如下：

[Parameter containing:
tensor([[[[[-0.0935,  0.0865],
           [ 0.2209, -0.2845]],

          [[-0.0739, -0.1571],
           [-0.0937,  0.0381]]]],



        [[[[ 0.3118,  0.0228],
           [ 0.0528,  0.3362]],

          [[ 0.2571, -0.2860],
           [-0.0248,  0.0413]]]],



        [[[[ 0.2757, -0.2870],
           [-0.0762, -0.0426]],

          [[-0.1114, -0.2718],
           [-0.2009,  0.2822]]]]], requires_grad=True), Parameter containing:
tensor([[[[[ 0.2868,  0.2352],
           [-0.0007,  0.0850]],

          [[-0.3403, -0.1515],
           [ 0.1643,  0.0257]]]],



        [[[[ 0.0032,  0.1932],
           [-0.0097, -0.2940]],

          [[-0.0324, -0.1837],
           [ 0.1531,  0.0724]]]],



        [[[[-0.0221, -0.0570],
           [-0.2833, -0.0661]],

          [[ 0.2186, -0.3194],
           [ 0.2589,  0.3500]]]]], requires_grad=True)]

    我们继续来分析这个结果，顺便解答上文中提到的疑惑。输出的每一层weight的维数是（3，1，2，2，2），这是为什么呢？因为输出的channel数是3，输入的channel数是1，因此每组filter个数只有一个，对应有3组；而每个filter的size是（2，2，2），因此最终构成了这样的维度。如果我们将输入channel数改为2，结果如下：

[Parameter containing:
tensor([[[[[ 0.0010,  0.2182],
           [ 0.1555, -0.2320]],

          [[-0.0709,  0.0921],
           [-0.1355,  0.0346]]],


         [[[-0.0892, -0.0357],
           [ 0.2133,  0.0405]],

          [[ 0.2069,  0.0941],
           [-0.0764,  0.1953]]]],



        [[[[ 0.2018, -0.2457],
           [-0.1158, -0.1205]],

          [[-0.0726,  0.0943],
           [ 0.0482, -0.0663]]],


         [[[-0.0650, -0.1981],
           [ 0.0315,  0.2254]],

          [[ 0.0718,  0.0973],
           [ 0.1592, -0.1737]]]],



        [[[[ 0.2142,  0.1077],
           [ 0.1751,  0.0160]],

          [[-0.1013,  0.0274],
           [ 0.1019,  0.1532]]],


         [[[-0.0256,  0.2313],
           [ 0.0342, -0.1884]],

          [[ 0.2467,  0.2350],
           [-0.0755, -0.0327]]]]], requires_grad=True), Parameter containing:
tensor([[[[[ 0.0423,  0.1196],
           [-0.0128, -0.2416]],

          [[-0.0489, -0.0292],
           [-0.1986,  0.0883]]],


         [[[-0.0821, -0.0545],
           [-0.0520,  0.0355]],

          [[-0.2379,  0.1677],
           [ 0.1035,  0.0444]]]],



        [[[[-0.1435, -0.1594],
           [-0.2482,  0.2464]],

          [[ 0.0265,  0.2154],
           [ 0.1938, -0.0941]]],


         [[[-0.2427,  0.1314],
           [ 0.2092,  0.0563]],

          [[-0.2206, -0.2361],
           [ 0.0972,  0.0308]]]],



        [[[[-0.1759,  0.2255],
           [-0.0830,  0.0939]],

          [[ 0.0004, -0.1010],
           [-0.2034, -0.0256]]],


         [[[-0.1844,  0.2256],
           [-0.1646, -0.0182]],

          [[-0.0159, -0.1947],
           [ 0.0426, -0.2360]]]]], requires_grad=True)]

    可以看到输出的每一层weight的维度是（3，2，2，2，2），即每组filter有两个，一共有三组。所以现在的卷积过程等于是：一组filter中的一个filter和一个channel的多个帧分别进行3维的卷积，相乘相加后得到一个数据，然后两个数据相加得到最终的一个数据。 等于是下面这幅图进行两次，一个channel对应进行一次，然后最后再加上两个数据相加的过程。

    所以最终的输出是三个绿色立方体堆叠在一起，形成了三个channel的feature map，即一个feature map不再是一个平面，而是一个三维的立方体了。在这里我们就可以看出，在3D卷积中，输出的feature map数（即输出通道数）仍然与卷积核的个数有关，不过在这里准确来说应该称为组数而不是个数，因为每一组可能会有多个filter，每组的filter数量就等于输入的通道数。

后言

    看到这里，小伙伴有没有清楚2D卷积和3D卷积的原理了呢？如果觉得博主写的还不错，麻烦小伙伴点赞收藏加关注，也欢迎在评论区发言，谢谢！