MTALAB学习笔记——二三维图像的基本画法
MATLAB是用于数学建模的一个软件,其名称为“matrix laboratory”(矩阵实验室)的缩写。顾名思义,MATLAB主要解决数学矩阵和图像相关的问题,其工作区与python类似,代码与C语言类似。
本篇文章的重点将会聚焦于MATLAB里的图像表达着重于讲解二三维曲线和显函数与隐函数的表述
二维图像
显性二维图像:
对每一个x有唯一与其对应的y即可以表示为 y = f ( x ) y=f(x) y=f(x)的图像,我们称之为显性函数
要表示这种函数只需写出y与x之间的关系式即可,在操作前,我们先认识几个重要的函数:
-
plot
plot(x,y):创建Y中数据对X中对应值的二维线图
plot(x,y,LineSpec):设置图像的线型和颜色等
eg:
plot(x,y1,'r--');输出y1=f(x)的图像,图像的线为红色虚线 -
Linspace
简单的说:x=linespace(a,b,c); 就是把a到b划分c份,然后每一份都存储到x数组中
-
hode on和hode off:将这个函数图像继续显示在坐标轴上因为在MATLAB中,若不提前写
hode on则新的图像就会把原来的图像顶替掉。
所以,当你想要一次性显示多个图像时,则需要将上一个图像hode on -
legend
在坐标图上添加图例 -
xlabel ylabel zlabel
为x,y,z,轴加上标签 -
colon, :
x = j:k:创建一个向量 x, [j,j+1,…,k]。
x = j:i:k创建一个等间距向量 x,以 i 作为元素之间的增量。向量元素大致为 [j,j+i,j+2i,…,j+mi],其中 m = fix((k-j)/i)。但是,如果 i 不是整数,则浮点算术运算的作用在于确定 colon 是否包括向量中的端点 k,因为 k 可能并不是正好等于 j+m*i。如果指定非标量数组,则 MATLAB 将 j:i:k 解释为 j(1):i(1):k(1)
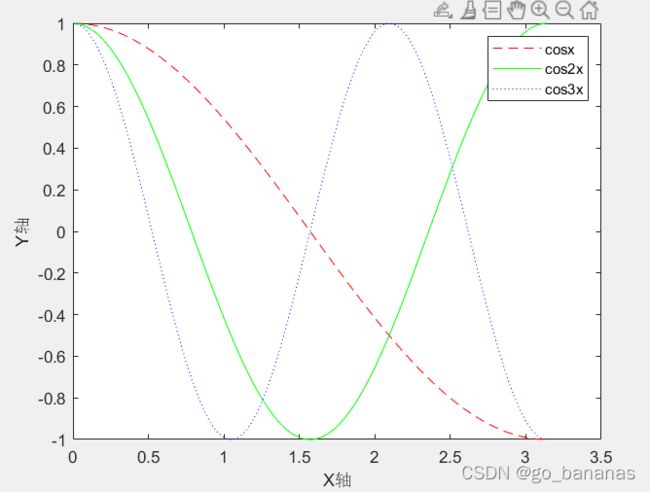
综合运用:我们根据前面的描述写下代码
x=linspace(0,pi,1000); %把x从0到pi分成1000份
y1=cos(x);
y2=cos(2*x);
y3=cos(3*x); %不同函数定义
plot(x,y1,'r--');
hold on; %防止新函数遮盖了之前的函数
plot(x,y2,'g-');
hold on;
plot(x,y3,'b:');
xlabel('X轴'); %标出x轴
ylabel('Y轴'); %标出y轴
legend('cosx','cos2x','cos3x'); %标出图例
隐性二维图像
对于绝大多数二维图像,一个x可能会对应多个y,此时函数图像再也不能写成 y = f ( x ) y=f(x) y=f(x)的形式,而是应该写成 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0的形式。此时我们又该如何描述我们的二维图像呢?
举个例子:我需要画出 x 2 + y 2 − 1 = 0 x^2+y^2-1=0 x2+y2−1=0的图像,在MATLAB里面的过程应该是怎样的呢?
- 将x,y,表示成二维网格(为什么不能把x,y分开写?看这个)
- 对每个二维网格上的点 ( x i , y i ) (xi,yi) (xi,yi)带入表达式的值记作 z i zi zi。
- 把 z i zi zi的等高线中 z i = 0 zi=0 zi=0的那条线取出来
- 最后的结果就是 x 2 + y 2 − 1 = 0 x^2+y^2-1=0 x2+y2−1=0的图像了
实际操作如下:
运用到的函数:
- contour :等高线相关函数,返回等高线
- meshgrid :网格线
- axis
PS:在计算 x ∗ x x*x x∗x时,不能写X*X而是要写X.*X(因为这里的X是矩阵,要用点乘)
写下代码
[X,Y] = meshgrid(-2:0.01:2 , -2:0.01:2);%把x,y从-2到2每隔0.01个单位分隔画网格
Z = X.^2+Y.^2-1;%作出Z关于X,Y的表达式
v = [0,0];%等高线为0
contour(X,Y,Z,v);
axis('equal');%使得x,y轴单位长度相等
参数方程确定的二维图像
还有些情况,我们会发现我们得到的曲线方程是 :
f ( x , y ) = { x = f ( t ) y = g ( t ) f(x,y)=\left\{ \begin{matrix} x=f(t) \\ y =g(t) \end{matrix} \right. f(x,y)={x=f(t)y=g(t)
这一类方程又如何在MATLAB中表示呢?其实大致过程和显函数区别不大。
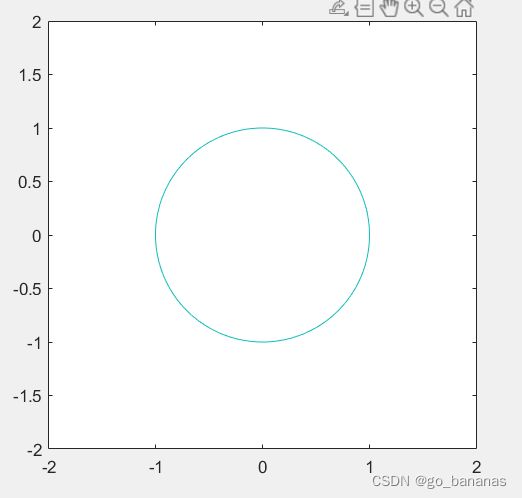
下面给出一个画单位圆的例子
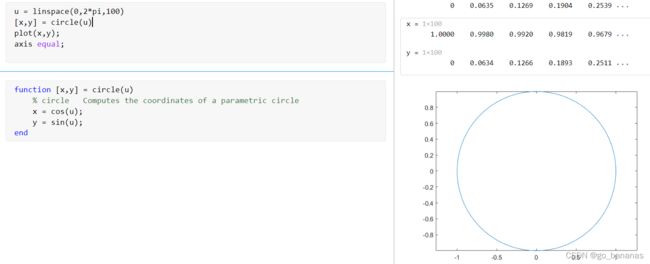
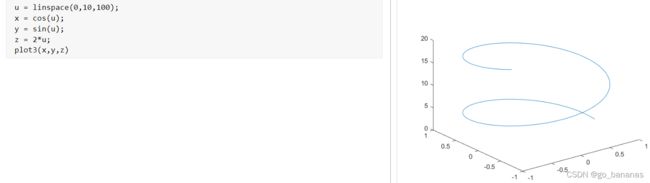
三维函数同理:
三维图像
显性三维图像
显性三维图像比较易于理解,在这里就不过多赘述。
只需注意函数contour,surf(类似于plot)shading
写下代码
x=linspace(-2*pi,2*pi,200);%定义x的取值范围
y=linspace(-2*pi,2*pi,200);%定义y的取值范围
[X,Y]=meshgrid(x,y)%建立网格
Z=myfunction(X,Y);
surf(X,Y,Z);%画出图像
shading interp;%定义图像格式
function res = myfunction(x,y)
res=sin(x)+cos(y);
end
就得到了 z = s i n ( x ) + c o s ( y ) z=sin(x)+cos(y) z=sin(x)+cos(y)的图像:
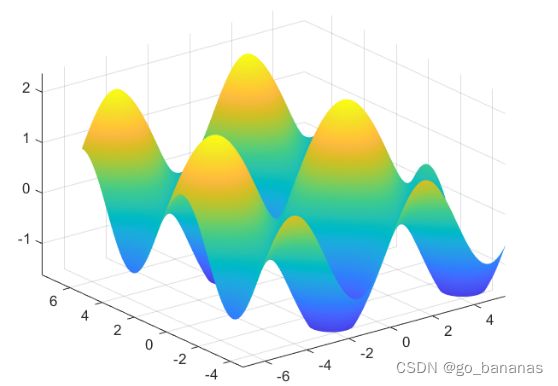
ps:你也可以把surf(X,Y,Z)改为contour(X,Y,Z)来把图像改为等高线。
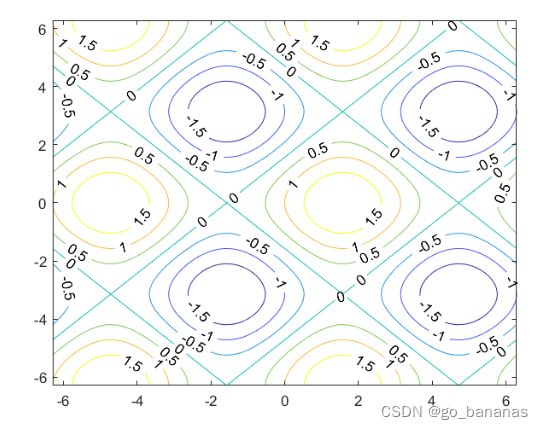
例如把上面代码的surf(X,Y,Z)改为contour(X,Y,Z,'ShowText',"on");就会出现下面的图像
隐性三维图像
在介绍隐性三维图像前,我们先认识一个函数isosurface你可以把它理解为一个找三维图像等值面的函数。
例如:
我现在需要画一个 x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x2+y2+z2=1的图像,这显然是一个隐性图像,我们的一般步骤如下:
- 把函数化为 f ( x , y , z ) = x 2 + y 2 + z 2 − 1 f(x,y,z)=x^2+y^2+z^2-1 f(x,y,z)=x2+y2+z2−1的形式。
- 我们的图像就是 f ( x , y , z ) f(x,y,z) f(x,y,z)在 f ( x , y , z ) = 0 f(x,y,z)=0 f(x,y,z)=0的一系列点构成的图像
- 利用isosurface函数画出图像即可
我们写出代码:
x=linspace(-5,5,100);
y=linspace(-5,5,100);
z=linspace(-5,5,100);
[X,Y,Z]=meshgrid(x,y,z);%做出x,y,z的三维网格
V=myfunction(X,Y,Z);
isosurface(X,Y,Z,V,0);%画出图像
axis('equal');%令坐标轴长度相等
function res = myfunction(x,y,z)
res=x.*x + y.*y + z.*z -1;
end
参数方程确定的三维图像
对于这样一类图像: x = f ( u , v ) ; y = g ( u , v ) ; z = h ( u , v ) x=f(u,v);y=g(u,v);z=h(u,v) x=f(u,v);y=g(u,v);z=h(u,v)
我们又因该如何来描绘呢?
其实方法和显性图像类似,举个例子:
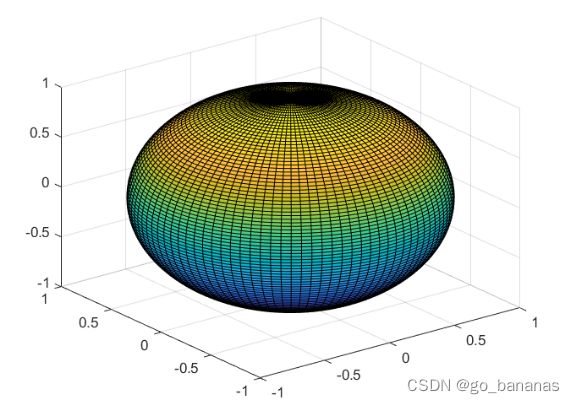
x = sin u cos v , y = sin u sin v , z = cos u , u ∈ [ 0 , π ] , v ∈ [ 0 , 2 π ] x = \sin u \cos v, y = \sin u \sin v, z = \cos u, u \in [0,\pi], v \in [0,2\pi] x=sinucosv,y=sinusinv,z=cosu,u∈[0,π],v∈[0,2π]
我们一样按照显性函数的描述方法写下代码:
u = linspace(0,pi,100)
v = linspace(0,2*pi,100)
[U,V] = meshgrid(u,v)
[X,Y,Z] = sphereparam(U,V)
surf(X,Y,Z)
function [x,y,z] = sphereparam(u,v)
x = sin(u).*cos(v);
y = sin(u).*sin(v);
z = cos(u);
end
得到图像:
以上就是二三维图像的基本画法了。
我们总结一下,不难发现:
- 对于显性函数和参数函数:描绘起来很简单,主要是熟悉各种函数的用法。
- 对于隐性函数:主要是掌握等值面的思想。