【题解】NKOJ——分治练习赛

A 组队参赛

问题描述
一年一度的信息学竞赛NK校赛即将开始，何老板在组织安排报名工作。
南开信竞队分为小学、初中、高中三个梯队:
小学梯队有N个队员，年龄分别是 $A_1$,$A_2$…$A_N$
初中梯队有N个队员，年龄分别是 $B_1$,$B_2$…$B_N$
高中梯队有N个队员，年龄分别是 $C_1$,$C_2$…$C_N$
比赛是组队参赛，三人一队，要求每只队伍里面必须要有小学、初中和高中各一人。同时，要求每个队中，小学队员的年龄<初中队员的年龄<高中队员的年龄。
何老板想知道，总共可能的组队方案有多少种？请你帮他算一算。两种组队方案中，至少存在一个不相同的同学，即被认为是不同方案。

输入格式
第一行，一个整数N
接下来三行，每行N个整数，分别表示每个梯队的队员年龄：
$A_1$,$A_2$…$A_N$
$B_1$,$B_2$…$B_N$
$C_1$,$C_2$…$C_N$
输出格式
一个整数，表示不同的组队方案总数。

1<=N<=10⁵
1<=$A_i$,$B_i$,$C_i$<=10⁹

---

因为是算方案数，看数据范围因该是一个O(N log(N))的算法，所以很容易想到先对三个数组排序，
再枚举B数组二分查找A中比它小的和C中比它大的再乘起来即可。

代码：

#include
#include
#define H 100005
using namespace std;
long long A[H],B[H],C[H],N;
long long Ans;
int main(){
	scanf("%lld",&N);
	for(int i=1;i<=N;i++)scanf("%lld",&A[i]);
	for(int i=1;i<=N;i++)scanf("%lld",&B[i]);
	for(int i=1;i<=N;i++)scanf("%lld",&C[i]);
	sort(A+1,A+1+N);
	sort(B+1,B+1+N);
	sort(C+1,C+1+N);
	for(long long i=1;i<=N;i++){
		long long t=B[i];
		long long a=lower_bound(A+1,A+1+N,t)-A;
		long long c=upper_bound(C+1,C+1+N,t)-C;
		Ans=Ans+(a-1)*(N-c+1);
	}
	printf("%lld",Ans);
}

---

B 外地比赛

问题描述
何老板带着信竞队的k个同学出去外地打比赛。
到达目的地后，何老板就找了一家酒店，准备住下。酒店工作人员告诉何老板，由于酒店一些房间已经有客人入住了，何老板和同学们的房间可能没法全都挨在一起。
酒店共有n个房间，房间编号1到n，编号相邻的房间间距为1,每个同学单独入住一个房间。
何老板想要在这n间房中找k+1间空房住下，但是为了同学们们的安全，必须让同学们们离着何老板尽可能最近。
现在已知这n间房的入住情况（0表示没有人，1表示有人），现在要你帮助何老板安排入住：
保证同学们都能入住的情况下，让离何老板最远的房间与何老板的房间距离尽可能近。

输入格式
第一行，两个整数n和k (1 ≤ k < n ≤ 100000)
第二行，一个长度为n的01串，依次表示1到n号房间的入住情况。

输出格式
一个整数，表示距离何老板最远的同学的距离。

---

看题目：
保证同学们都能入住的情况下，让离何老板 最远 的房间与何老板的房间距离 尽可能近 。

显然的二分提示，所以我们这里二分一 个同学们离何老板最远的距离的最大值（也就是答案）。
对于每一个答案，我们只需要O(N)的时间复杂度带入验证即可。

代码：

#include
#include
#define H 100005
using namespace std;
int N,K,A[H];
int R[H],Ans;
bool check(int Mid){
	memset(R,0,sizeof(R));
	for(int i=1;i<=Mid+1;i++)if(!A[i])R[Mid+1]++;
	for(int i=Mid+2;i<=min(2*Mid+1,N);i++)if(!A[i])R[Mid+1]++;
	for(int i=Mid+2;i<=N;i++){
		R[i]=R[i-1];
		if(!A[i-Mid-1])R[i]--;
		if(i+Mid<=N&&!A[i+Mid])R[i]++;
	}
	for(int i=Mid;i<=N;i++)if(!A[i]&&R[i]>=K+1)return 1;
	return 0;
}
int main(){
	scanf("%d%d",&N,&K);
	for(int i=1;i<=N;i++)scanf("%1d",&A[i]);
	int l=0,r=N,Mid;
	while(l<=r){
		Mid=l+r>>1;
		if(check(Mid))Ans=Mid,r=Mid-1;
		else l=Mid+1;
	}
	printf("%d",l);
}
//R[i]：以i为中心半径为Mid的长度中可以居住的房间个数

PS:好像三分老师房间的位置也可以通过此题

---

C 部落划分

传送门
问题描述
聪聪研究发现，荒岛野人总是过着群居的生活，但是，并不是整个荒岛上的所有野人都属于同一个部落，野人们总是拉帮结派形成属于自己的部落，不同的部落之间则经常发生争斗。只是，这一切都成为谜团了——聪聪根本就不知道部落究竟是如何分布的。
不过好消息是，聪聪得到了一份荒岛的地图。地图上标注了N个野人居住的地点（可以看作是平面上的坐标）。我们知道，同一个部落的野人总是生活在附近。我们把两个部落的距离，定义为部落中距离最近的那两个居住点的距离。聪聪还获得了一个有意义的信息——这些野人总共被分为了K个部落！这真是个好消息。
聪聪希望从这些信息里挖掘出所有部落的详细信息。他正在尝试这样一种算法：
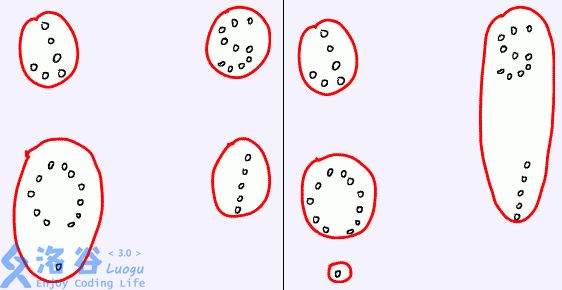
对于任意一种部落划分的方法，都能够求出两个部落之间的距离，聪聪希望求出一种部落划分的方法，使靠得最近的两个部落尽可能远离。 例如，下面的左图表示了一个好的划分，而右图则不是。请你编程帮助聪聪解决这个难题。

输入格式
第一行包含两个整数N和K(1< = N < = 1000,1< K < = N)，分别代表了野人居住点的数量和部落的数量。
接下来N行，每行包含两个正整数x,y，描述了一个居住点的坐标(0 < =x, y < =10000)

输出格式
输出一行，为最优划分时，最近的两个部落的距离，精确到小数点后两位。

---

如何把不同的部落合并到一起？ " 并查集 "
如何计算所有部落的之间的最小距离的最小值的最大值？"二分答案"
我们二分出距离的最小值的最大值‘ Mid ’，枚举图中所有点之间的连边，如果两个点之间的距离小于Mid就把两个点用并查集合并起来；最后统计不同的集合个数，如果小于K，加大Mid，否则减小Mid

代码：

#include
#include
#define H 1005
#define db double
using namespace std;
int N,K,fa[H];
db X[H],Y[H],Ans,L,R,Mid;
int gf(int x){return x==fa[x]?x:fa[x]=gf(fa[x]);}
db Dis(db x1,db y1,db x2,db y2){
	return sqrt( (x1-x2)*(x1-x2) + (y1-y2)*(y1-y2) );
}
int main(){
	scanf("%d%d",&N,&K);
	for(int i=1;i<=N;i++)scanf("%lf%lf",&X[i],&Y[i]);
	for(int i=1;i<=N;i++){
		for(int j=1;i<=N;i++)R=max(R,Dis(X[i],Y[i],X[j],Y[j]));
	}
	int T=60;
	while(T--){
		Mid=(L+R)/2.0;
		for(int i=1;i<=N;i++)fa[i]=i;
		for(int i=1;i<=N;i++){
			for(int j=1;j<=N;j++){
				if(i!=j&&Dis(X[i],Y[i],X[j],Y[j])=K)L=Mid;
		else R=Mid;
	}
	printf("%.2lf",R);
}
//好像kruakal最小生成树也可以完成此题,这里就不写了

---

D 楼房重建

问题描述
小A的楼房外有一大片施工工地，工地上有N栋待建的楼房。每天，这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆，数自己能够看到多少栋房子。

为了简化问题，我们考虑这些事件发生在一个二维平面上。小A在平面上(0,0)点的位置，第i栋楼房可以用一条连接(i,0)和(i,Hi)的线段表示，其中Hi为第i栋楼房的高度。
如果这栋楼房上存在一个高度大于0的点与(0,0)的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。

施工队的建造总共进行了M天。初始时，所有楼房都还没有开始建造，它们的高度均为0。
在第i天，建筑队将会将横坐标为Xi的房屋的高度变为Yi(高度可以比原来大—修建，也可以比原来小—拆除，甚至可以保持不变—建筑队这天什么事也没做)。
请你帮小A数数每天在建筑队完工之后，他能看到多少栋楼房？

输入格式
第一行两个正整数N,M
接下来M行，每行两个正整数Xi,Yi

输出格式
M行，第i行一个整数表示第i天过后小A能看到的楼房有多少栋

---

显然，对于第 $i$ 和第 $j$ 栋建筑($i$<$j$)，当且仅当($H_j/j$>$H_i/i$)时，才可以既看到$i$建筑又看到$j$建筑。
那么显然我们要求的是对于每一栋建筑，我们算出它的斜率($H_j/j$)，我们要求的是对于$1.....N$ 栋建筑其斜率的最长上升序列的长度。
由于题目有单点修改操作，所以我们需要依靠某种数据结构来完成此题。

此题有两种数据结构的方法，线段树版，分块版

线段树版 代码：

#include
#include
#define H 100005
#define db double
#define int long long
using namespace std;
struct node{db Max;int Tot;}T[H*12];
int N,M;
int ask(int L,int R,int P,int X,db W){
	if(L==R){
		return T[P].Max>W;
	}
	if(T[P].Max<=W)return 0;
	int Mid=L+R>>1;
    if(T[P<<1].Max>W) return T[P].Tot-T[P<<1].Tot+ask(L,Mid,P<<1,X,W);
    else return ask(Mid+1,R,P<<1|1,X,W);
}
void add(int L,int R,int P,int X,db W){
	if(L==R){
		T[P].Max=W;
		T[P].Tot=1;
		return;
	}
	int Mid=L+R>>1;
	if(X<=Mid)add(L,Mid,P<<1,X,W);
	else add(Mid+1,R,P<<1|1,X,W);
	T[P].Max=max(T[P<<1].Max,T[P<<1|1].Max);
	T[P].Tot=T[P<<1].Tot+ask(Mid+1,R,P<<1|1,X,T[P<<1].Max);
}
main(){
	scanf("%lld%lld",&N,&M);
	while(M--){
		int x,y;scanf("%lld%lld",&x,&y);
		add(1,N,1,x,db(y)/db(x));
		printf("%lld\n",T[1].Tot);
	}
}
//T[P].Tot 子树P节点所表示的区间中对答案(其斜率的最长上升序列的长度)的贡献的个数
//T[P].Max 子树P节点所表示的区间中的最大值

---

分块版 代码：
PHenning大佬的说法：

**神犇们都用的线段树QWQ本人太魔芋了只会用分块QWQ。
首先把楼房看成一个序列，每个数字是，这个应该没有问题吧QWQ。
先把序列分成块，对每一个块开一个vector，把这个块从左往右扫一遍，在vector中记录站在这个块的最左端能够看到的数字。例如一个块是，则vector中存的是。显然站在序列最左端能看到的数字一定可以在所有块的vector中找到。
假设某一次修改了第块中的某个数，那么前块能看到的数字都还是能看到，记录当前能看到的最大数字，然后从第块往后扫每一个块，对于每一个块，在vector中二分查找比大的数，计入答案，然后更新。
理论时间复杂度$O(m\sqrt{n}{\log }_{2}n)$。但是它不会T，也不会爆精度，WA了也是正常的QWQ。 **

附上大佬的代码：
b数组等于vector

#include
#include 
#include 
#include 
#include 
using namespace std; 
const int maxn=1e5+5; 
void rin(int &t) 
{t=0;char c=getchar();while(!isdigit(c))c=getchar();while(isdigit(c)){t=t*10+c-'0';c=getchar();}} 
int n,m,S,cnt[350],Size; 
double a[maxn],b[maxn]; 

void modify(int x,double y) 
{ 
    int i=(x-1)/S+1; 
    a[x]=y; 
    int r=min(n,i*S); 
    cnt[i]=0;
    for(int k=(i-1)*S+1;k<=r;k++)
    {
        if((a[k]!=0&&cnt[i]==0)||(cnt[i]!=0&&a[k]>b[(i-1)*S+cnt[i]]))b[(i-1)*S+(++cnt[i])]=a[k];
    }
} 

int query() 
{ 
    double tmp=0; 
    int ans=0; 
    for(int k=1;k<=Size;k++) 
    { 
        int x=upper_bound(&b[(k-1)*S+1],&b[(k-1)*S+1+cnt[k]],tmp)-(&b[(k-1)*S]); 
        ans+=cnt[k]-x+1; 
        if(x!=cnt[k]+1)tmp=b[(k-1)*S+cnt[k]]; 
    } 
    return ans; 
} 
int main() 
{ 
    rin(n);rin(m);S=sqrt(n);Size=n/S; 
    if(n%S)Size++; 
    int x,y; 
    for(int i=1;i<=m;i++) 
    { 
        rin(x);rin(y); 
        modify(x,(double)y*1.0/x); 
        printf("%d\n",query()); 
    }     
}

---

E 比赛评分

问题描述
Lj​最近参加一个选秀比赛，有N个评委参加了这次评分，N是奇数。
评委编号为1到N。每位评委给Lj​的分数是一个整数，评委$i$($1\le i\le N$)的打分为。
这次采用了一种创新的方法计算最后得分，计算规则是：
  最初N位评委排成一排，检查队伍排头的3位评委的评分，去掉一个最高分和一个最低分，剩下的一个评委移动到队伍最后，反复执行以上操作，直到队伍中的评委只剩一位，那么这个评委的打分就是Lj的最后得分。
由于有的评委年纪比较大了，不记得自己的位置了，现在有$M$($1\le M\le N-2$)个评委很快找到了自己的位置，剩下的$N-M$人找不到位置了，需要给他们重新安排位置。
由于Lj希望自己的得分尽可能高。请你帮忙计算出LJ最后得分可能的最大值。

输入格式
第一行为整数N和M，用空格分隔。表示有N位评委，其中M人的初始排列位置已经确定。

接下来M行中第i行($1\le i\le M$)为两个整数$D_i$和$P_i$，用空格分隔。

表示第i位评委的评分为Di，初始排列位置为队伍排头开始的第Pi位。 接下来$N-M$行中第i行为整数$D_i{+}_M$，表示评委(i+M)的评分为$D_i{+}_M$。 3 ≦ N ≦ 99 999，

1 ≦ M ≦ N - 2，
1$\le$$D_i$$\le$ 10⁹
1 ≦ Pi ≦ N (1 ≦ i ≦ M)，
Pi != Pj (1 ≦ i < j ≦ M)。

输出格式
输出一行，为1个整数，表示LJ得分的最大值。

分析： 如果只有三个分数 $D_i$,$D_j$,$D_k$ .如果我们想让最后的分数$\ge$Ans 的话，其充要条件是$D_i$,$D_j$,$D_k$中至少有两个数$\ge$Ans.

eps: $A[i]$：表示 $i$ 号评委的打分，如果i位置不确定，$A[i]$=0.

立即注意到： 答案$Ans$（最后的得分）得分 与 位置不确定的打分$\ge$$Ans$的评委个数有单调性 所以可以二分
我们设：
$Ans$：二分的答案
$优质评委$： 位置不确定的评委中，打分$\ge$$Ans$ 的评委
$F[i]$：使得$A[i]$单个位置（只看这个位置，不看前面位置）的值$\ge$$Ans$所需要的优质评委个数。
显然，我们可以得到如下式子：

if(A[i]==0)F[i]=1;//i号位置不确定所以需要1个优质评委
else if(A[i]>=Ans)F[i]=0;//A[i]已经>=Ans,不需要优质评委
else if(A[i]=Ans,赋值为无穷大

那么这对于我们解题有什么帮助呢？
这里有一个显然的贪心：
对于$F[i]$,$F[j]$,$F[k]$ $(i=j-1=k-2)$
从中会淘汰掉两个数值，为了使的留下来的数$\ge$$Ans$,我们需要付出的最小代价是
$min(F[i]+F[j],F[i]+F[k],F[j]+F[k],inf)$
最后用队列维护一下即可

代码：

#include
#include
#define H 100005
#define inf 123456789
using namespace std;
int A[H],E[H],L,R,Mid,tot,Ans;
int N,M;
bool check(int Mid){
	for(int i=1;i<=N-M;i++)if(E[i]>=Mid)tot++;
	queue Q;
	for(int i=1;i<=N;i++){
		if(A[i]==0)Q.push(1);
		else if(A[i]>=Mid)Q.push(0);
		else Q.push(inf);
	}
	while(Q.size()>1){
		int x1=Q.front();Q.pop();
		int x2=Q.front();Q.pop();
		int x3=Q.front();Q.pop();
		Q.push(min(x1+x2,min(x1+x3,min(x2+x3,inf))));
	}
	if(Q.front()<=tot)return 1;
	else return 0;
}
int main(){
	scanf("%d%d",&N,&M);
	for(int i=1;i<=M;i++){
		int w,p;scanf("%d%d",&w,&p);
		A[p]=w;
		R=max(R,w);
	}
	for(int i=1;i<=N-M;i++){
		scanf("%d",&E[i]);R=max(E[i],R);
	}
	int T=60;
	while(T--){
		Mid=(L+R)/2,tot=0;
		if(check(Mid))Ans=L,L=Mid+1;
		else R=Mid-1;
	}
	printf("%d\n",Ans-1);
}

---

有什么不懂的，欢迎留言。(只要蒟蒻我会)