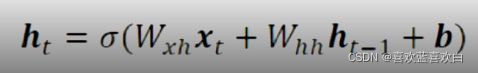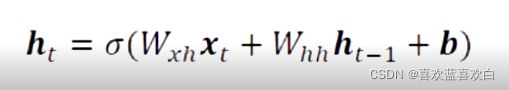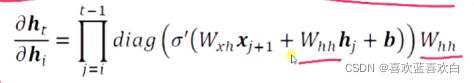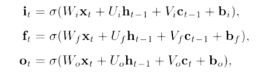循环神经网络（内含LSTM、GRU实战）

目录

1. Embedding

2. RNN介绍

       2.1. memory机制

3. SimpleRNN （实战）

4. 循环神经网络的问题

5. LSTM

6. LSTM层在情感分类（实战）

7. GRU （理论+实战） 

8. 深层循环神经网络

---

1. Embedding

        以前讲的都是常用与空间性的学习，而时序性的学习则需要使用循环神经网络。

        那项声音，文字等序列是如何表示的呢？

        可以利用序列的相关性表示。

        这就可以讲到一个Embedding了。

        Embeddin层：

1. 通过计算相似度，在空间中查找最近邻。
2. 实现高纬稀疏特征向量像低稠密特征向量的转换。
3. 训练好的embedding可以当作输入深度学习模型的特征。

        常用Embedding方式：

        Word2vec（使用最为广泛的词嵌入方法）：速度快，效果好，容易扩展，简单。

        

         一般Word2vec分为两个模型：        

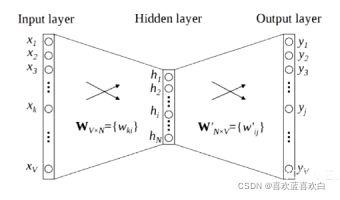
        CBOW

1.      1. 输入层： 上下文单词的onehot。（要训练此的上下文）
2. 所欲的onehot分别乘以共享的输入权重矩阵W
3. 所有的向量相加求平均作为隐层向量
4. 乘以输出权重矩阵W
5. 得到向量经过激活函数处理得到概率分布
6. 概率最大的index所指示的单词为预测的中间词（target word）与true label的onehot作比较，误差越小越好（更具误差更新权重矩阵）
7. 假设我们此时的到的概率分布已经达到了设定的迭代次数，那么输入层的每个单词与矩阵W相乘得到的向量的就是我们想要的词向量。

       TF实战实例：

        注意：输入进去的不是真的字，而是是一个索引！！！

        

import tensorflow as tf
from tensorflow import keras

x = tf.range(5)
x

x = tf.random.shuffle(x)
x

net = tf.keras.layers.Embedding(input_dim=5,output_dim=4)
# input_dim 输入单词的个数 是可处理的容量，要大于真正的输入，这次实验是>5
# output_dim 是一个向量有多少个数表示。我理解为特征。

net(x)

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data()

(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

tf.keras.datasets.imdb.get_word_index()

#Embedding 输入必须是等长的。因此要对数据做一些处理。
x = tf.keras.preprocessing.sequence.pad_sequences(x_train , maxlen=250)
len(x[0]),len(x_train[0])

net = tf.keras.layers.Embedding(input_dim=90000,output_dim=4)

net(x) # 25000个句子，一个句子250个单词，一个单词由4个词向量组成

---

情感分析，具体演示循环神经网络过程：

        把序列通过数字输入，经过Embedding层转为词向量，词向量是[句子数，单词长度，词向量长度（特征）] 。

---

2. RNN介绍

        

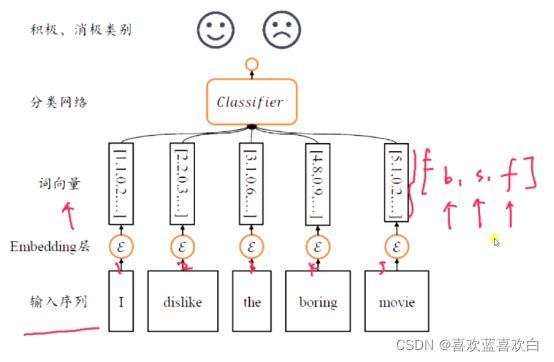
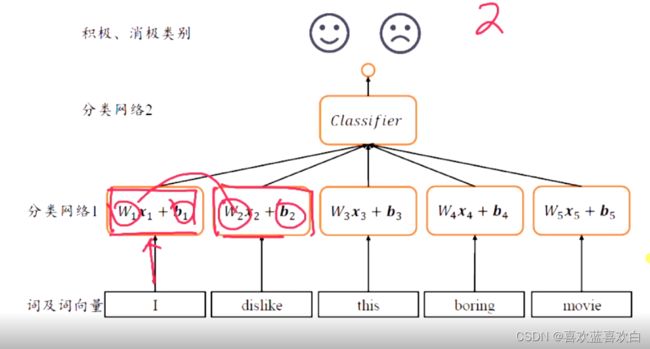
        首先思考这样的二分类全连接神经网络可行吗？

        没一个单词对应的词向量经过一个网络层，最后再经过一个合并，然后最后再进行一个类别的区分。可这样的话，和以前的相同的，参数量也会过多。同事每个句子也没法保证每个句子的长度保一样。这样构建的全连接网络层是动态变化的。是不太好的。而且每个输入之间是没有关系的。比如x1只会和x1有关系，但是一个句子是一句话，他们之间是有关系的，我们不能捕捉这种关系。因此我们要逐一解决这种问题。

        解决思路：

        以前在卷积就提出过，权值共享的思路，既能减少网络的参数量，但是这一段话的句子还是将句子分开几个部分理解，还是不能理解句子的整体特征。

       2.1. memory机制

        那么怎么获取网络的整体语义信息呢？或者说怎么将特征逐渐积累，直至最后提取整个句子的信息呢？我们提出了memory机制。

        如果说，网络提供一个单独的网络特征词向量，我们每次提取网络的词向量特征的时候，同时刷新memory，直到序列的最后。

         将memory机制实现成一个状态张量h：

         除了每个词都有一个句子的共享权值w_xh，还有一个w_hh是一个额外增加的权重。

        最后一个h就能够很好的代替整个句子的语义信息。

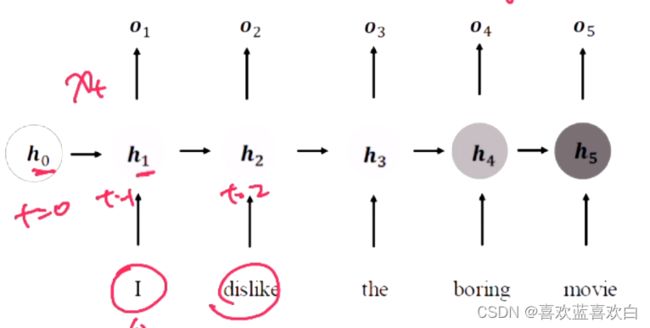
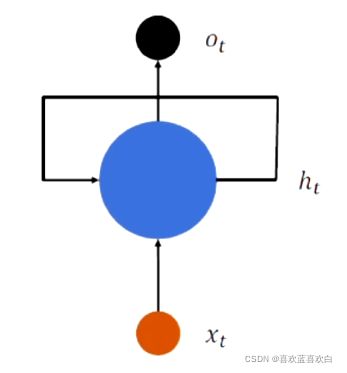
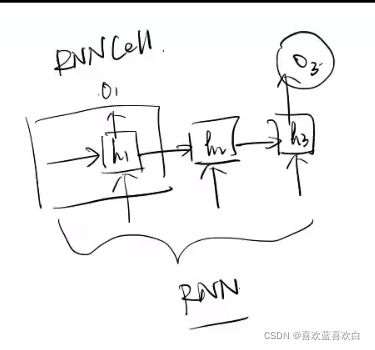
        基于上述的过程，有人提出了这样一个网络层：

        在每一个时间戳上都进行一个输入输出的循环计算，在每个时间戳上，网路都会接受一个输入xt(词向量),输入网络的xt会与上一个网络的输出ht-1，计算得到该网络的输出，简要公式是：

        其中f是一个网络逻辑，是一个参数集合。

        这样的网络模型，我们既可以保留之前句子的信息，也能有当前词的信息。

        一个基本的CNN是：激活函数里面的，就是CNN的网络逻辑。

        模型简化：

3. SimpleRNN （实战）

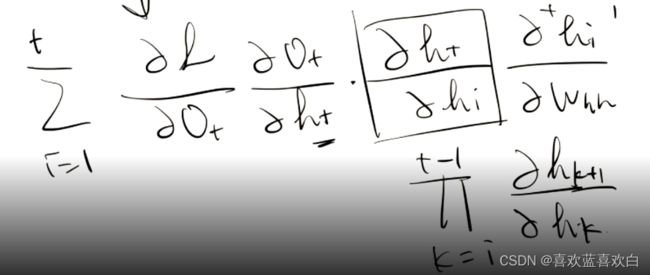
        先介绍梯度的计算：

        上图模型最后得到的O，可以与真实值进行比较，然后得到一个loss，然后对loss进行反向传播求得梯度，再对参数进行更新。不过循环神经网络一个很大的问题就是，我们求得的梯度过程中要进行一个Whh的连乘计算，计算起来比较慢。

        

       SimpleRNNCell：

         SimpleRNNCell是指只完成了一个时间戳上的计算（因为每个时间戳都有一个输出，这个输出与h有关），而SimpleRNN是一整个CNN过程。

        输入的形状是什么呢？总共的训练集是：[多少句话,句子单词数,每个词的Embedding后的词向量长度]，训练是在句子每个单词序列上展开的，则输入的是：[句子单词数，embedding后的特征]。

        那么每次运算后我们希望能够降维，只要利用 [b,f] @ [f,n]，设置n大小即可。

        CNN还可以纵向进行多层训练。因为out也是一个输出，把out作为新层的输入即可。

        具体计算方式既可以先纵向，再横向。当然也可以先横向再纵向。 

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

cell = layers.SimpleRNNCell(3) # 输出的个数，即n
cell.build(input_shape=(None,4)) #4是输入的，3是输出神经元的个数
cell.trainable_variables

# 【4，3】是输出有四句话，每句话被Embedding到3个词向量长度。
# 【3，3】是当前的whh,是一个额外的向量。

h_0 = [tf.zeros([4,64])] # 4个句子，做计算后姜维的到64个词向量大小
x = tf.random.normal([4,80,100]) # 4句话，每句话80个单词，100个Embedding后的大小。

# 沿着80展开，让【4,100】 @ 【100,64】
x_1 = x[:,0,:] #第一个词
x_1.shape

cell = layers.SimpleRNNCell(64)
#两个输出，一个out，一个h，h还要进入下一层进行计算。
out_1,h_1 = cell(x_1,h_0)
#这里两者完全相等
out_1==h_1

out_1.shape

h = h_0
for x_i in tf.unstack(x,axis=1):
    out , h = cell(x_i , h)

out

x_1 = x[:,0,:]

cell_0 = layers.SimpleRNNCell(64)
cell_1 = layers.SimpleRNNCell(32)

h_0 = [tf.zeros([4,64])] #把他转换为一个列表
h_1 = [tf.zeros([4,32])]

for x_i in tf.unstack(x,axis = 1): # 再s上扩展
    out_0 ,h_0 = cell_0(x_i,h_0)
    out_1 ,h_1 = cell_1(out_0,h_1)

out_1

layer = layers.SimpleRNN(64)

out = layer(x)
out

model = keras.Sequential([
    #return_sequences=True，除了最末层以外，每个时间戳伤都要返回一个状态的输出
    layers.SimpleRNN(64,return_sequences=True),
    layers.SimpleRNN(32)
])

model(x)

4. 循环神经网络的问题

        当层数过多的时候，RNN的长期依赖问题：梯度爆炸和梯度弥散（消失）

        上述梯度中有一个连乘计算，当Whh的最大特征值大于1时，就会出现梯度爆炸（因为指数级的计算是很庞大的）。而Wt 与等于 Wt-1时就会出现梯度弥散现象

        使用权重衰减或梯度截断（裁剪）解决

        权重衰减是通过给参数增加l1范数或l2范数的正则来限制参数的取值范围，从而使得γ <= 1，

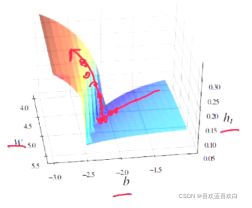
        梯度截断是另一种有效的启发式方法，当梯度的模大于一定阈值时，就将他截断成为一个较小的数。

         如下图这种情况，如果不进行截断，会一下子上去，因此要在之前就要进行截断。

        除了以上提到的梯度爆炸问题，梯度消失问题是循环神经网络的最主要的问题。RNN最大的问题就是，当层数增多时，之前的记忆会逐渐模糊！！！即短时记忆。除了改变学习率，减小层数，等方法外，最直接的方法就是改变学习的模型        

        解决方案：让过去得输出不仅作为输入，还要作为输出的一部分保留信息。

• 改进模型1：乘法保持信息。但是梯度爆炸的速度就更加快了。一般都会有限制，使用也只用于控制。
• 改进模型2：加法保持信息。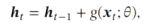会丢失非线性激活的性质，降低模型表达能力。所以我们可以把ht-1放进g（）中，即改进3.
• 改进模型3：增加非线性关系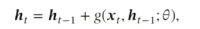：即存在线性关系，又是非线性关系。所以可以缓解改进2的丢失非线性激活的性质，但仍然存在梯度爆炸问题以及记忆容量问题。

        因为每次记忆都会储存，则会出现即已饱和现象。随着时间，ht会越来越大，但是机器能存储的记忆容量是有限的，则越来越多时，也会出现记忆丢失现象。

        为了解决这两个问题，我们可以引入门控这一个概念。        

---

5. LSTM

         相比传统的CNN来说，LSTM更擅长于处理长时间的记忆。

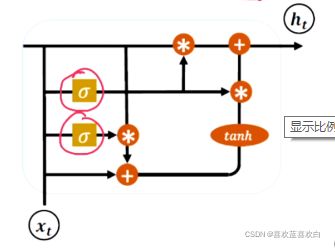
        LSTM的原理：

        与RNN的区别：

         1. 除了输入的xt和ht-1之外，还加入了一个长时记忆单元c，而h控制的是一个短时的记忆。 

         2. 还有门控机制：输入门、遗忘门、输出门，通过三个门来控制信息的流转。

---

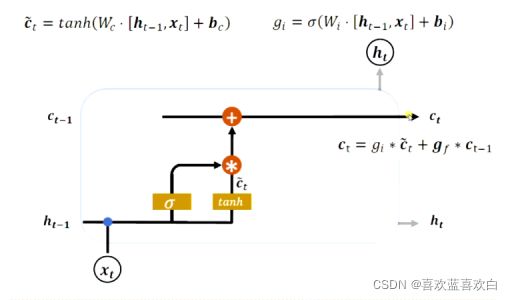
        门控机制：

         输出有多少取决于门控值！我们称门控程度为：门控值，其可以控制阈值。首先把门控值压缩到（0，1）之间，当sigmoid输出为0时是完全关闭，1时是完全打开。

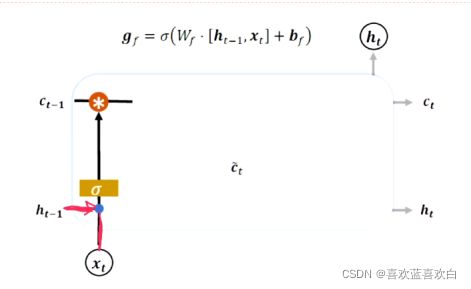
        输入门： 刷新Memory

        控制LSTM对输入的接收程度，不全接收所有输入。

        ht-1是之前记住的20个单词，xt表示新的10个单词。经过tanh将这两个输入做了一个融合（或者说对输入做一个非线性变换，提取所有的输入的信息，最后输出）。tanh还可以把值都压缩至（-1,1）之间。有点像归一化。而值是阀门，可以用sigmoid产生（0,1）之间的值。

        遗忘门：

        Ht-1相当于短时记忆，Ct-1相当于长时记忆。遗忘门来决定长时记忆能记住多少。记住多少也是取决于ht-1和xt。而以前的记忆到底能记住记住多少个，就要看遗忘门。

        当前的输出，能全部输出吗？这要看输出门。

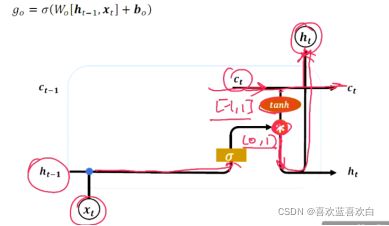
        输出门：

        ct-1是直接输入，但是输入ht-1与xt则与输入门差不多，是部分输入。

输入门	遗忘门	LSTM行为
0	1	只能记忆
1	1	综合输入和记忆
0	0	清除记忆
1	0	输入覆盖记忆

        LSTM变形：

        1. 没有遗忘门

        2. 耦合输入门和遗忘门：输入门和遗忘门，有一定的相同功能，同时使用两个门会有些冗余，于是可以将两者耦合

        3.peephole连接： 把长时 的记忆也放进RNN中 。

6. LSTM层在情感分类（实战）

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

# 我们希望每个输入的长度都是相同的
x_train = keras.preprocessing.sequence.pad_sequences(x_train,maxlen=250)
x_test = keras.preprocessing.sequence.pad_sequences(x_test,maxlen=250)

# 整合成一个train_db，和test_db
train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))

train_db = train_db.shuffle(10000).batch(128 , drop_remainder=True) # drop_remainder多余的就不要了
test_db = test_db.shuffle(10000).batch(128 , drop_remainder=True)

class myLSTM(keras.Model):
    def __init__(self):
        super().__init__()
        #可以吧两个输入整个作为一个输入
        self.state_0 = [tf.zeros([128,64]) , tf.zeros([128,64])]
        self.state_1 = [tf.zeros([128,32]) , tf.zeros([128,32])]

        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)

        self.lstm_cell_0 = layers.LSTMCell(64)
        self.lstm_cell_1 = layers.LSTMCell(32)

        self.fc = layers.Dense(1)

    def __call__(self,inputs, *args, **kwargs):
        x = self.embedding(inputs)
        state_0 = self.state_0
        state_1 = self.state_1
        for x in tf.unstack(x,axis = 1):
            out_0 , state_0 = self.lstm_cell_0(x,state_0)
            out_1 , state_1 = self.lstm_cell_1(out_0,state_1)
        x = self.fc(out_1)
        x = tf.sigmoid(x)

        return x

model = myLSTM()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history = model.fit(train_db,epochs=10)

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

        也可以直接写在一个LSTM中：

class myLSTM(keras.Model):
    def __init__(self):
        super().__init__()
        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)
        self.lstm_0= layers.LSTM(64 ,return_sequences=True) #与RNN同理除了最后一个前面所有都需要一个return
        self.lstm_1 = layers.LSTM(32)
        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        x = self.lstm_0(x)
        x = self.lstm_0(x)
        x = self.fc(x)
        x = tf.sigmoid(x)

        return x

        LOSS收敛图：

         测试机上的正确率：

---

7. GRU （理论+实战） 

        前面说了，LSTM主要是为了解决梯度弥散的问题，但是其有个缺点就是计算复杂。

        三个门复杂，参数量大。如何进行优化呢？

        经过一些研究发现，遗忘门在LSTM中是最重要的一个门，这个已经在2018年的论文中得到证实，甚至发现只有遗忘门在多个数据集上能有良好的表现，甚至有些数据集上只有遗忘门的网络更优于3个门都有的网络。

        在很多简化版LSTM中GRU门控循环网络是引用最广泛的LSTM变种。

        GRU把状态向量，输出向量做出了一个合并。统一成为一个向量h，且把门控减少到2

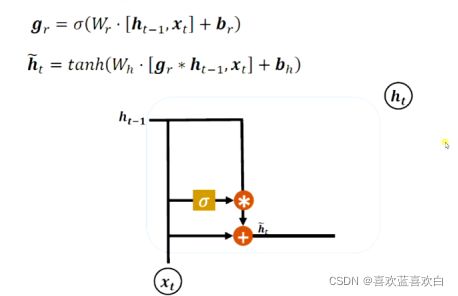
        复位门（重置门）：控制上一个时间戳的状态ht-1进入GRU网络的一个量 。他不再像LSTM中用2个输入c和h，这里只有一个输入h。

         至于上一时段的记忆通过什么来控住阈值呢？还是g作为门控。至于Wr和br只是对记忆h和输入的信息做一个特征提取。然后上一个记忆ht-1经过门控g的控制，再与当前信息x作为输入经过Wr和br的特征提取，最后经过一个激活函数tanh即可。

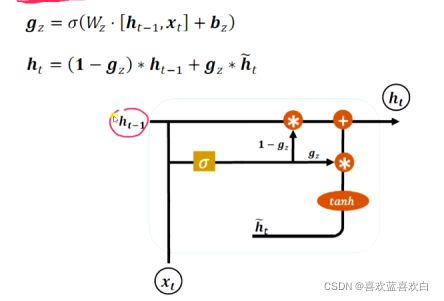
        更新门：控制上一个时间戳上的记忆ht-1和新的ht_hat。

       

        首先对上一个记忆ht-1和当前信息进行特征提取，并经过一个sigmoid，g这里也是阀门。ht-1经过的阀门与ht_hat加起来为1，即此消彼长，二者相互竞争的关系，最后流向ht。

        具体代码：

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.imdb.load_data()
(x_train.shape, y_train.shape), (x_test.shape, y_test.shape)

# 我们希望每个输入的长度都是相同的
x_train = keras.preprocessing.sequence.pad_sequences(x_train,maxlen=250)
x_test = keras.preprocessing.sequence.pad_sequences(x_test,maxlen=250)

# 整合成一个train_db，和test_db
train_db = tf.data.Dataset.from_tensor_slices((x_train,y_train))
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test))

train_db = train_db.shuffle(10000).batch(128 , drop_remainder=True) # drop_remainder多余的就不要了
test_db = test_db.shuffle(10000).batch(128 , drop_remainder=True)

class myGRU(keras.Model):
    def __init__(self):
        super().__init__()
        #可以吧两个输入整个作为一个输入
        self.state_0 = [tf.zeros([128,64])]
        self.state_1 = [tf.zeros([128,32])]

        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)

        self.gru_cell_0 = layers.GRUCell(64)
        self.gru_cell_1 = layers.GRUCell(32)

        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        state_0 = self.state_0
        state_1 = self.state_1
        for x in tf.unstack(x,axis = 1):
            out_0 , state_0 = self.gru_cell_0(x,state_0)
            out_1 , state_1 = self.gru_cell_1(out_0,state_1)
        x = self.fc(out_1)
        x = tf.sigmoid(x)

        return x

model = myGRU()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history = model.fit(train_db,epochs=10)

import matplotlib.pyplot as plt

plt.plot(history.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.show()

model.evaluate(test_db)

class myGRU(keras.Model):
    def __init__(self):
        super().__init__()
        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)
        self.gru_0= layers.GRU(64 ,return_sequences=True) #与RNN同理除了最后一个前面所有都需要一个return
        self.gru_1 = layers.GRU(32)
        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        x = self.gru_0(x)
        x = self.gru_1(x)
        x = self.Drop(x)
        x = self.fc(x)
        x = tf.sigmoid(x)

        return x

# 为了防止过拟合
可以加入Dropout
# 为了防止梯度爆炸
可以加入正则化项

class myGRU(keras.Model):
    def __init__(self):
        super().__init__()
        self.embedding = layers.Embedding(input_dim=100000,output_dim=100)

        self.gru_0= layers.GRU(64 ,return_sequences=True) #与RNN同理除了最后一个前面所有都需要一个return
        self.gru_1 = layers.GRU(32)

        self.bn = layers.BatchNormalization()
        self.Drop = layers.Dropout(0.5)
        self.fc = layers.Dense(1)

    def call(self,inputs):
        x = self.embedding(inputs)
        x = self.gru_0(x)
        x = self.gru_1(x)
        x = self.Drop(x)
        x = self.fc(x)
        x = tf.sigmoid(x)

        return x

model = myGRU()
model.compile(
    optimizer=keras.optimizers.Adam(0.001),
    loss=keras.losses.BinaryCrossentropy(from_logits=True),
    metrics=['accuracy']
)

history = model.fit(train_db,epochs=10)

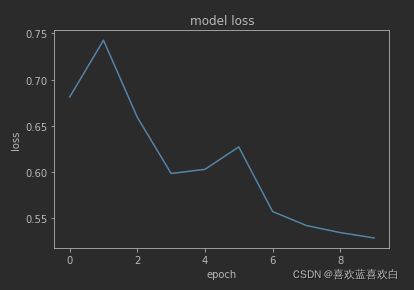
        Loss1:

        训练集和测试集上的准确率：0.943，0.8345。

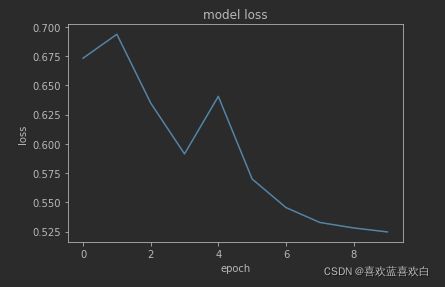
        改进后Loss2（没有加入正则项，因为发现加入正则项无法收敛）：

         训练集和测试集上的准确率：0.9529，0.8516 （10个epoch）0.9732，0.8598（20个epoch）0.9605，0.8397（学习率=0.0004，再训练10次）

8. 深层循环神经网络

        之前说过CNN由于梯度爆炸和梯度弥散，很难进行深层训练。而LSTM主要就是用来解决梯度弥散，至于梯度爆炸可以用梯度截断的方式。

        因为GRU（LSTM的改版）解决了梯度弥散的问题，于是循环神经网络就可以变得更加深层。

        深层循环神经网络有以下几种形式：

•         堆叠循环神经网络：就是之前的纵向计算，之前是堆叠了两层。当然还可以继续堆叠。
•         双向循环神经网络：顺序方向和逆序方向分别训练，后进行纵向叠加。

        应用场景：

         RNN的特点：引入记忆，但是长程依赖问题，或是记忆容量问题，很难深层。