java广度优先求解最短路径_算法:广度优先搜索(BFS)(最短路径)
算法:广度优先搜索(BFS)(最短路径)算法:广度优先搜索(BFS)(最短路径)
我们先看一个案例:
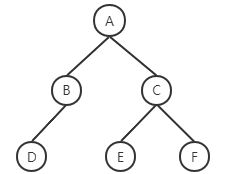
遍历一个树结构,按层次输出树的节点内容,即:欲求 A B C D E F。
实现方式便是从根节点(A)向下遍历,先获取A,其次是A的子节点B和C,其次是B的子节点D……
这种遍历树结构或者图结构的方法被称作广度优先搜索(BFS),与之对应的先遍历到最下层子节点的是深度优先。
起步:BFS基本解法
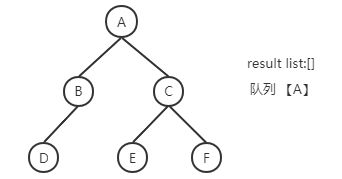
BFS核心采用队列的数据结构,例如上面的树结构中,解法为:
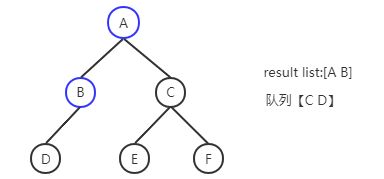
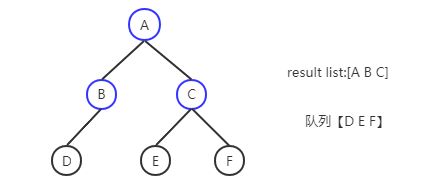
A进队列->A出队列 B、C进队列->B出队列 D进队列 ->C出队列 E、F进队列-> D、E、F出队列
如果想要区分层次边缘,使用count参数即可。
解法步骤(蓝色部分为已经处理完的节点):
详细解法代码为:
//定义树节点
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
public List> levelOrder(TreeNode root) {
List> result = new ArrayList<>();
if (root == null) {
return result;
}
Queue queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
List oneLevel = new ArrayList<>();
// 每次都取出一层的所有数据
int count = queue.size();
for (int i = 0; i
TreeNode node = queue.poll();
oneLevel.add(node.val);
if (node.left != null){
queue.add(node.left);
}
if (node.right != null){
queue.add(node.right);
}
}
result.add(oneLevel);
}
return result;
}
进阶:BFS基于图的示例-最短路径
例题
给定两个单词(beginWord 和 endWord)和一个字典,找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则:
每次转换只能改变一个字母。
转换过程中的中间单词必须是字典中的单词。
说明:
如果不存在这样的转换序列,返回 0。
所有单词具有相同的长度。
所有单词只由小写字母组成。
字典中不存在重复的单词。
你可以假设 beginWord 和 endWord 是非空的,且二者不相同。
示例:
输入:beginWord = "hit",endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
输出: 5
解释: 一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog",
返回它的长度 5。
基本解法——普通的BFS
不难看出此题是一个很经典的图结构:
很容易想到这种题可以用广度优先解法,从start处的hit遍历每一种可能,直到匹配到cog。解法如下(其中提到了剪枝//TODO,因为此题实际不是要走全部节点的广度优先):
class Solution {
public int ladderLength(String beginWord, String endWord, List wordList) {
Queue queue = new LinkedList();
//初始值入队列
queue.offer(beginWord);
int result=1;
//观察题目,其实要求结果在词典中
if(!wordList.contains(endWord)){
return 0 ;
}
while(true){
int length=queue.size();
//全部单词遍历也没结果
if(length==0){
return 0;
}
for(int i=0;i
String a=queue.poll();
//成功转换到了结果值
if(canChange(a,endWord)){
return result+1;
}
for(int z=0;z
if(canChange(a,wordList.get(z))){
queue.offer(wordList.get(z));
//不要重复使用词典中的词,这只会徒增时间复杂度,这是一种 剪枝手段
wordList.set(z,null);
}
}
}
result++;
}
}
/***
* 校验是否符合转换的标准
**/
private boolean canChange(String a,String b){
if(b==null){
return false;
}
int i=0;
for(int q=0;q
if(a.charAt(q)!=b.charAt(q)){
i++;
}if(i>1){
return false;
}
}
return true;
}
}
更快的解法——双向BFS、通用状态
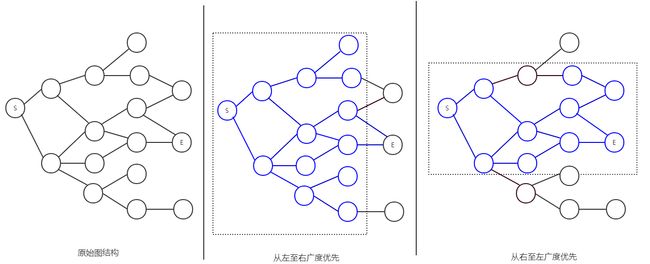
对于上面的单向搜索,当图结构越发复杂时,随着搜索深度的提高,其搜索每一层锁付出的代价也越大,为此我们可以考虑从两端开始分别进行广度优先遍历,这样在多数情况下能节省很多时间,免去不必要的搜索(事实上,这也是一种剪枝手段)。
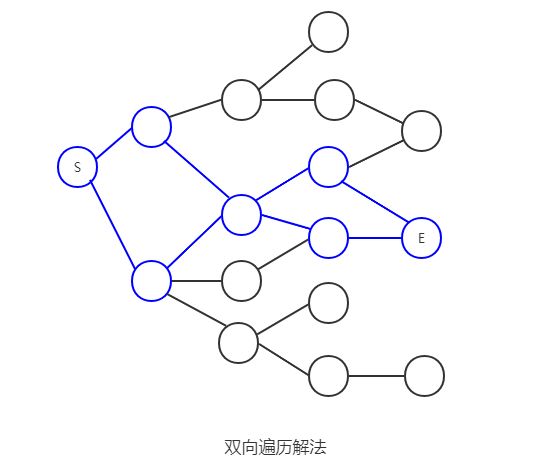
在上面的图例中,分别使用了从起点(S)和终点(E)进行广度优先搜索的结果,便利了很多多余的节点,但是如果我们使用双向BFS,两边以同时进行搜索(可以每次选择子节点最少的端搜索),效率一般会大大提升:
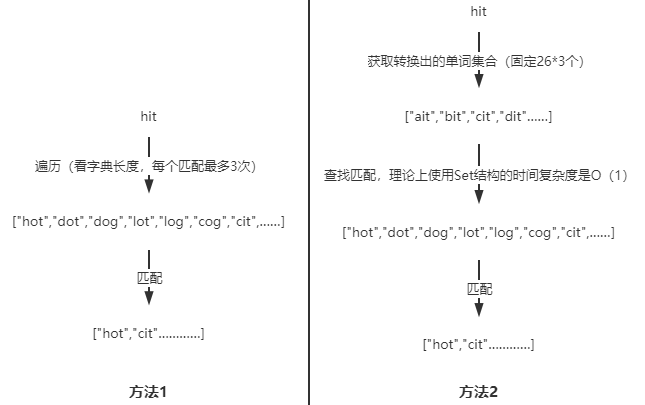
同时,我们可以根据相应的测试用例改变单词匹配的方式,因为字母数量是已知的(26个),但是字典数据的长度却是未知的,我们使用上面的比较方法即下图的方法1,在首次出队列进行单词匹配时,其时间复杂度为O(M*N),M代表词典长度,N代表单词的字母数。如果我们使用方法2,对于每一个节点不是去遍历整个词典,而是去遍历符合其转换条件的所有单词,并且查看单词是否在词典中,其时间复杂度固定为)O(26*N),虽然每一个节点的遍历复杂度都是一样的,但是对于词典长度较长的用例,显然后者的效率更高且稳定。再加上双端便利,效率提升很大。
最终的解法:
class Solution {
public int ladderLength(String beginWord, String endWord, List wordList) {
if (wordList == null || !wordList.contains(endWord)) {
return 0;
}
//转为Set提高查询速度
Set allWord = new HashSet<>(wordList);
//将beginWord加入list
wordList.add(beginWord);
//begin的队列 初始化
Queue queue1 = new LinkedList<>();
//因为用这种方式不知道什么时候才会匹配到,所以需要一个Set记录遍历过的元素
Set visited1 = new HashSet<>();
queue1.add(beginWord);
visited1.add(beginWord);
//end的队列 初始化
Queue queue2 = new LinkedList<>();
Set visited2 = new HashSet<>();
queue2.add(endWord);
visited2.add(endWord);
int depth = 0;
while (!queue1.isEmpty() && !queue2.isEmpty()) {
//将节点更少的作为1队列 交换二者
if (queue1.size() > queue2.size()) {
Queue temp = queue1;
queue1 = queue2;
queue2 = temp;
Set set = visited1;
visited1 = visited2;
visited2 = set;
}
//遍历上面拿到的节点最少的层
depth++;
int size = queue1.size();
while (size-- > 0) {
String poll = queue1.poll();
char[] chars = poll.toCharArray();
//遍历poll的每个字符
for (int i = 0; i
//保存第i个字符,判断结束后需要还原
char temp = chars[i];
//将poll的每个字符逐个替换为其他字符
for (char c = 'a'; c <= 'z'; c++) {
chars[i] = c;
//判断替换后的单词
String newString = new String(chars);
if (visited1.contains(newString)) {
continue;
}
if (visited2.contains(newString)) {
return depth + 1;
}
//如果替换后的单词,存在字典中,则入队并标记访问
if (allWord.contains(newString)) {
queue1.add(newString);
visited1.add(newString);
}
}
//还原第i个字符
chars[i] = temp;
}
}
}
return 0;
}
}