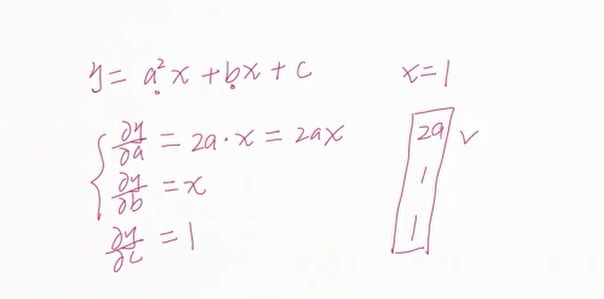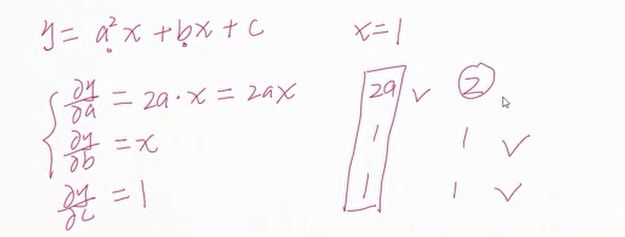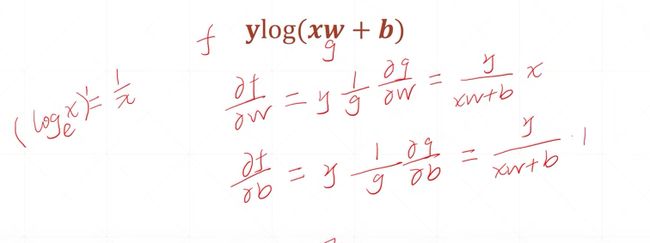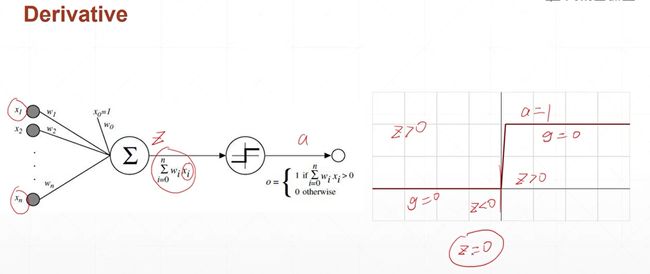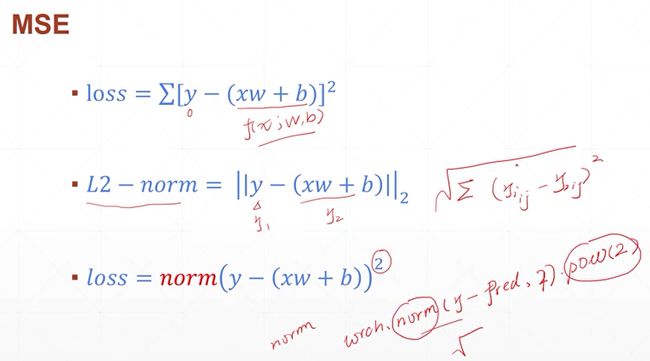网易云课程:深度学习与PyTorch入门实战
网易云课程:深度学习与PyTorch入门实战
- 01 深度学习初见
-
- 1.1 深度学习框架简介
- 1.2 pytorch功能演示
- 2开发环境安装
- 3回归问题
-
- 3.1简单的回归问题(梯度下降算法)
- 3.3回归问题实战
- 3.4 分类问题引入
- 3.6手写数字识别体验
- 4Pytorch基础
-
- 4.1张量数据类型
- 4.2创建Tensor
- 4.3 索引与切片
- 4.4 维度变换
- 5随机梯度下降
-
- 5.1什么是梯度?
- 5.2 什么是梯度
-
- 局部极小值
- 鞍点
- 影响搜索过程的其他因素
- 5.3 常见函数的梯度
- 激活函数与loss梯度1
- 激活函数与Loss梯度2
- 6.5 感知机的梯度推导-1
- 6.6 感知机的梯度推导-2
- 6.7 链式法则
- 6.8 MLP反向传播
- 6.9 2D函数优化问题
- 7 神经网络与全连接层
- 9卷积神经网络CNN
-
- 9.1什么是卷积?
- 9.2 卷积神经网络
- 9.3 池化层
- 9.4 Batch Norm
- 9.5 经典卷积神经网络(LeNet5、AlexNet、VGG、GoogleNet)
-
- 9.5.1 LeNet-5(80年代)
- 9.5.2 AlexNet
- 9.5.3 VGGNet
- 9.5.4 GoogleNet
- 9.6 ResNet(何凯佲)
- 9.7 InceptionNet
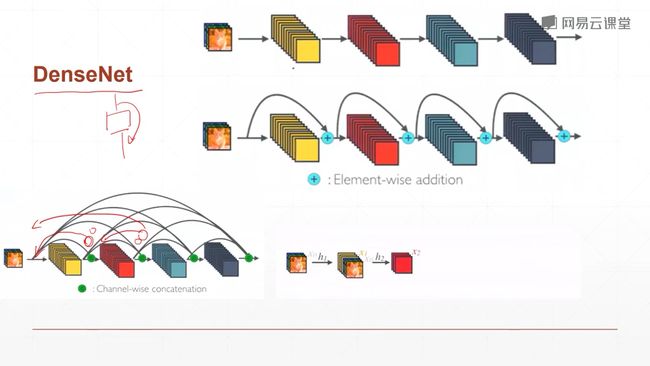
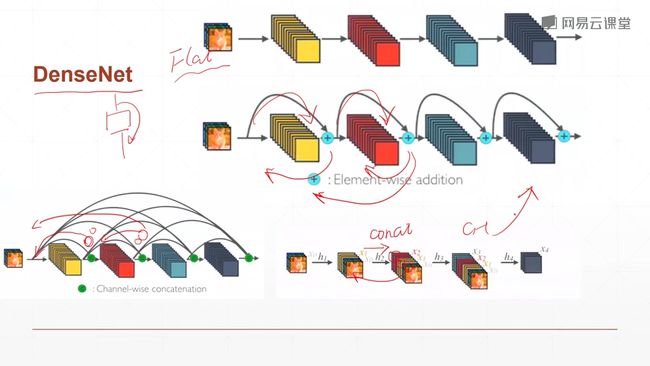
- 9.8 DenseNet
- 9.10 nn.Moudle
01 深度学习初见
1.1 深度学习框架简介
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MAdBgtvY-1627353571007)(5EB9766392EB434A9C110DCA000E54D9)]
Nn.linear 是全连接层
relu是relu层
Conv2d是卷积操作
Softmax激活函数
Sigmoid激活函数
CrossEntropyLoss交叉熵的损失激活函数
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WyASig9a-1627353571009)(AF7EFC6E2C9343B7BB74C62AC636D57D)]
梯度下降算法就是,求导的迭代过程,每次我们求出一个导数,我们就在当前的x上面的值,减去导数的值,得到一个新的$ x' $的值,这样就完成了一次求导迭代的过程,也就是一次梯度下降的过程。我们最终要求得的就是使得lossfunction最小的$ x^* $
1.2 pytorch功能演示

学术;pytorch
工业界:TensorFlow2

pytorch:
自然语言处理:nlp包
计算机视觉:torchVision包
图卷积:pytorch geometric / fast.ai
pytorch训练好的模型,可以用ONNX协议,轻松部署


第一次在cuda上运行的时候,要完成一些环境的初始化,所以时间会边长,而在此运行时,反映的就是比较准确地时间了,加速了50倍左右。
2开发环境安装
3回归问题
3.1简单的回归问题(梯度下降算法)



closed form solution
可以精确求解的问题,称之为closed form solution
闭环问题? 用高斯消元法
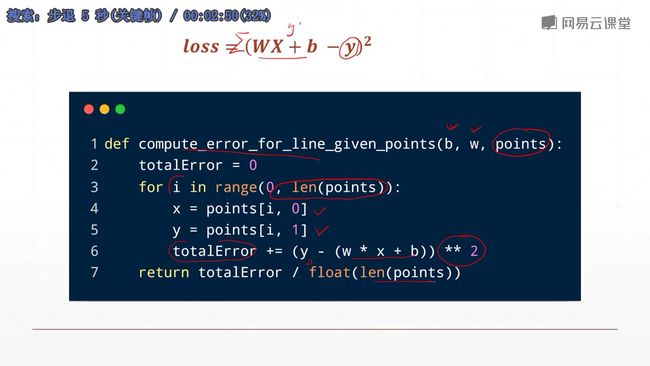
然后在现实生活中,我们拿到的数据往往都是带有一定的噪声的,或者说带有一定的观测误差,人会有自己的主观意志在里面,这使得我们拿到的数据样本会不太一样。就比如说我们在原本的wx+b上面,加上一个随机的高斯噪声,这个高斯噪声是采样自均值为0.01,方差为1的高斯分布。distribution(分布),这个噪声相对而言是比较小的,但是因为它的存在,使得我们拿到的这个数据样本,相对而言是准确的。这里下面的几个绿色的公式,我们拿到了两个方程,我们同样是可以求解的。因为我们引入了误差,我们希望多观测几次这个数据,来求得一个平均的稍微好一点的解,这样子的话,与其观测两个数据点,得到的误差可能会稍微有一点大,我们通过观测一组数据,通过观测者一组数据,来求得这一组数据之上的,整体表现好的这样的一个解,这样的一个解,虽然可能不是closed form solution,但是它被我们经验证明了可以有良好的表现。已经可以达到我们的需求了,因此对于实际的问题我们往往都不会,像初中时候那样,只给出两个观测样本,就比如说方程1和方程2,我们就可以求解了。这往往是不准确的,我们往往会拿到这样的100组或者是1000组这样的方程组,然后通过求解这1000或者100个方程组,整体表现好的一组参数量,来把它作为我们一组方程的解。我们把它写成矩阵形式就是这样子,(WX+b - y)^2,然后我们希望求解的是什么呢?我们为什么要把它写成这个样子呢?大家想想我们刚才讲过的那个例子,我们使用梯度下降算法是求什么?是求这个函数的最小值,但是对于Y = WX+b这个方程来说,我们是要求y的最小值吗?不是,我们是要求y与wx+b这两个差最小,因为我们希望,我们求解的这个w和b的参数使得wx+b这个值更加接近于我们真实的y的值,因此我们并不是要求y的极小值,而是希望求y和wx+b,之间的和最小。我们通过这个方法来衡量他们之间的差距。比如说我们希望求y和wx+b之间差的平方和最小,通过求他们两个之间的平方和最小,我们令这个新的函数称为loss函数,这个loss函数的值最小,我们就达到了使得y和wx+b非常接近的目的,为什么是这个样子的呢?

首先我们来看一下,这个loss 函数是不是大于等于0的,当这个loss function等于0的时候,也就是y等于wx+b的时候。因此我们求y = wx+b的最小值也就是求 y =wx+b,或者说y 近似于wx+b,这样也就得到了你想要的那样一个参数w和参数b,我们用非常真实的模型,来生成一系列的数据,那我们怎么生成呢?
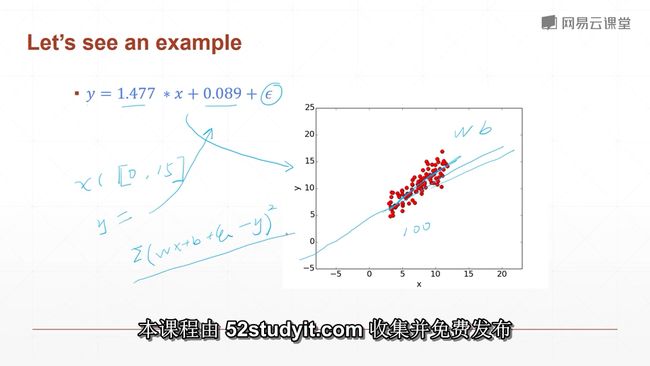
比如说x我们从0-15之间,随便sample出来值,它对应的y的值也会sample出来,就等于上面的公式,我们通过这个具体的模型,sample出来一系列的值,比如说这里面有100个点,我们现在是拿到了一个有高斯噪声的100个数据的采样样本,我们知道这100个高斯噪声,也知道这个函数是怎么生成的,但是我们假设不知道,为什么呢?
因为在实际当中,我们是不知道这个模型是什么样子的。我们通过观察并且给出一定的假设,我们假设这个函数是符合线性分布的。就比如说它是如图的直线,我们就是要求出具体的w和b的参数,使得这条直线跟整体的这个误差比较小,我们怎么衡量这个误差呢?
就是用均方差,就是用我们求得的wx+b+艾普斯冷的值和真实的y值之间的平方和差最小,我们把这个标准作为我们要优化的目标,也就是说我们要求这个函数的极小值,我们把下面那个函数稍微的正式化一下。

对于一个具体的方程,我们要求解的参数是w和b,然后我们观测到的样本是x和y,xi表示我们第i个观测到的样本,我们通过借助于梯度下降的方法,梯度下降可以帮助我们求解一个极小值。我们这里是希望wx+b逼近于y,因此我们构建一个[y-(wx+b)]这样一个新的函数,来求这个新的函数的极小值,也就达到了我们x趋近于b这样一个目的,我们给这个新的函数取名为loss函数,在Loss函数取得极小值的时候,w和b的值,也就是我们要求解的值,我们通过最小化这个Loss function,使得我们求解了一个比较合适的解,合适解我们叫做w’(w派)和 b派(b’),这样,对于一个新的观测样本,w’x’+b’与y’之间的符合度是非常非常高的,因为我们就是这么求解的,即使不知道y·,我们也能够给出一个y’(y派)的估计。
上面谈到的那个方程是非常容易求解的,现在我们来可视化的看一下,整个求解的过程,我们通过调整不同的w和b,会生成不同的loss值,如图示w轴和b变化的轴,我们是希望求解Loss最小的这个点,最小的这个点大概在什么位置?如图蓝色的点是比较低的点,红色的点是比较高的点,我们通过对这个图片的感测,大概可以目测出最低点的位置。所以说,如果Lossfunction能够可视化的话,我们就可以非常直观的来观察出loss function最低点的w和b的值,但是现实生活中往往都不能够可视化,因为我们的x的维度是非常非常高的,导致我们这个w的维度也非常非常高,因此我们很难在三维的空间中把函数loss function的图像画出来,大家可以看一下这个曲面是比较光滑的,是有一个固定的下降区间,你从任何一个点走走走,总会走到这样一个大概的范围里面,因为他有一个全局极小解,而且这个函数就像一个碗一样,你从这个碗里的任何一个地方滴一滴水的话,这个水滴总会顺着这个碗壁,流流流,流到碗底。这样的函数叫做凸函数。
对于凸函数,它有一个专门的学科来讲解如何优化凸函数,就叫做凸优化。对理论感兴趣的话可以稍微去关注一下这些书籍。但是我们做deeplearnning算法,一般来说,对这方面的深入了解会少一些,我们就直接用现成的这些优化器就可以了。这个函数,即使是非凸函数,我们也能够找到一个局部最小值,这个局部最小值根据经验往往来说,已经发现效果比较好了,因此我们即使是一个局部极小值,我们也可以先用着。

![]()

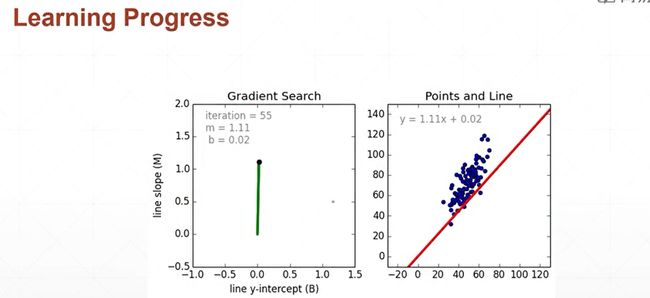
现在我们来动态的来看一下,w和b的动态求解过程,右边的这幅图就是说,我们从一个随机的初始点,比如说我们把w和b都随机地初始化为0,然后我们在每一处对w和b来求导,来更新这个w的值,大家可以看一下,这条红色的线,也就是y=wx + b 对应的一次函数不断向左逆时针走,看左边的图,我们会发现,我们更新100次之后,w和b的值,已经比较接近于我们的理论值了,这两幅图也比较直观地描述了整个学习的过程,这也是我们希望看到的,我们希望看到的就是,一条这样的直线穿过整个数据集,是的整体误差偏小。
现在我们来看一下,我们刚刚求解的问题,我们刚刚求解的问题是什么? 我们要预测wx+b的一个值公式中各个参数的值,我们现在已经拿到了一些样本,我们通过观察这一系列的样本,来推测一个w和b的参数,使得我们对于任何一个给出的xn的值我们能够很好地预估yn,这就是我们最终的目的,我们这里的y的取值范围,大概是属于一个整体的实数空间,比如说是-无穷到+无穷,我们把这种案例,也就是y的取值范围是实数空间的这种案例,叫做linnie regresion线性回归。别看它的名字这么复杂,它其实非常非常简单,它就是说他要预测的一个值是连续的值,那什么是连续的值? 就比如说我们要预测某一个数值的大小,它是连续的吧,我们要估计,年龄的大小,0-100,虽然说,他并不是在整个的实数空间,但是他在0-100的空间,我们也可以理解为y的值是连续的,因此它也是regression,然后,我们可以预测某一个指数,就比如说恒生指数啊,股票的指数呀,某一方面的指数呀,这些都是regression的问题,然后与regression相对的一个叫logistic regression,逻辑回归是什么意思呢? 就是在原本的linear regression的基础上加了一个回归函数,也就是加了一个压缩函数,它会将y从负无穷到正无穷的一个去见范围压缩到0-1的这样一个范围,因此逻辑回归会把原来的一个实数的连续取值空间压缩到0-1的范围,那0-1有什么好处?首先0-1表示一个概率的问题,比如二分类的硬币正反面问题,我们需要的不是实数域的取值范围,而是一个0-1的取值范围,用0表示正面,用1表示反面。因此我们就可以用,logistic regression
来解决这个二分类问题。 再比如说0-9的一个手写数字识别问题,这种问题有什么特点呢? 就比如说我有十个点,每个点代表了当前这个lable的概率大小,因此它有一个这样的特点,就是说这十个点的概率加起来会等于一,对于这种问题,它的每一个点的范围是0-1,但是他还有另外一个属性,就是所有的点的概率加起来等于1,这就是分类问题和逻辑回归问题的一个小区别,逻辑回归问题对应的某个点的概率是0-1,他没有说所有的点的概率加起来要是0-1,它是单独的处理就可以了。而线性回归最简单,它是默认所有的取值点都是连续的,你可能不是属于负无穷或者正无穷,但是你是一个比较大的连续空间。
3.3回归问题实战
给位同学,我们上节课讲解了梯度下降算法,我们通过分析一个简单的二元一次方程组,讲解了我们初中时代,使用消元法的clossed fond解法,然后我们通过添加了一个高斯噪声,来模拟现实生活中遇到的一些问题,添加了噪声以后,如果只观测1-2个数据,这样子得出的模型,往往具有非常大的随机性,我们通过sample一些类的数据,来求解一个线性模型,使得这个线性模型,在这一系列数据上总的误差和最小,得到的模型往往具有非常好的鲁棒性。
鲁棒是Robust的音译,也就是健壮和强壮的意思。它是在异常和危险情况下系统生存的关键。比如说,计算机软件在输入错误、磁盘故障、网络过载或有意攻击情况下,能否不死机、不崩溃,就是该软件的鲁棒性。所谓“鲁棒性”,是指控制系统在一定(结构,大小)的参数摄动下,维持其它某些性能的特性。
模型能够透过噪声发现数据的真实的形态。

对于这种预测值属于连续实数空间的问题,
我们给它取个名字,称之为称之为线性回归 Linear Regression。
对于预测值在0-1之间的连续空间的问题,我们换了一个名字,称之为logistics regression,它就是在一般的线性回归模型的基础上加了一个额外的logistics function,这也就是我们常讲的sigmoid function,它的作用就是把x属于负无穷到正无穷之间的范围,压缩到0-1之间,这种压缩特表适合表达概率问题。比如说二分类的硬币,正面还是反面的一个概率问题,以及多分类问题的手写数字识别,我们除了知道它的数字范围在0-1之间外,它还有一个额外的约束,就是要求所有的输出节点之间的总的数据概率之和为1。这个就更加符合一个多分类问题。然后我们取概率最大的一个点作为预测值。
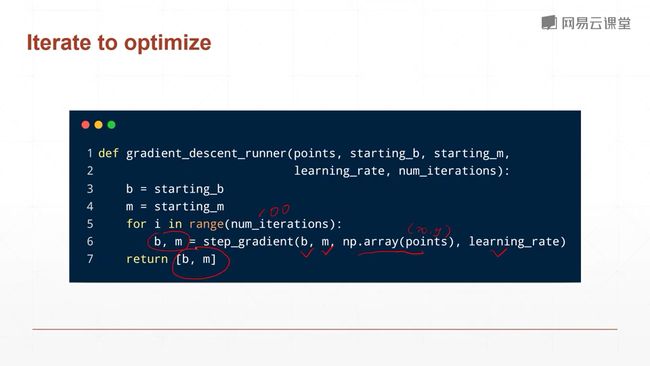
OK,至此,我们已经讲解了如何使用numpy,通过梯度下降的算法来求解一个简单的二元一次方程组,下一节课,我们将使用真正的梯度下降算法去求解一个现实的问题,因为对于这样一种简单的二元一次方程组,可能大家看起来非常的学术化,仅限于一些看起来像是比较简单的例子,下一节可,我们将使用梯度下降算法来求解一个非常具有现实意义的问题。比如说邮政编码的识别,比如说数字车牌的识别。
3.4 分类问题引入
例如数字0,它含有7000张照片,涵盖各种风格样式,可以每个数字用6000来训练,1000来测试。所以就是60K训练,10K来测试。
这样划分的目的是,防止过拟合,过于理想的结果。
现在我们来看一下,怎么计算loss? 要计算Loss,首先要知道我们这个h3,如果作为最后一个输出的话,那么 它怎么表达我们想要表达的lable信息呢?首先我们想到的第一种方法是,对于数字0-9,我们用一个维度,9个数字来表达,因此我们这里h3的输出就可以表示成H3:[1,1],第一个1表示的是照片数量,第二个1表示的就是0-9的一个数字,对于图片来说,lable是1或者lable是3,他们之间是没有相关性的。我们可以对数字进行one-hot编码,这种编码方式就没有大小关系。
如上图,假设我们有一个十维的点,她的真实的lable,建设如图右边[0 1 0 0 0], 根据二维的欧式距离的一个算法,我们这里十维的点也可以直接相减。然后再求一个平方和,这就是欧氏距离的算法。欧氏距离适合于2维、三维、…十维等等这样的向量之间的差距。

我们pred值不采用0-9的数字来表示,因为我们刚刚讲了,我们采用一个10维的向量来表示。
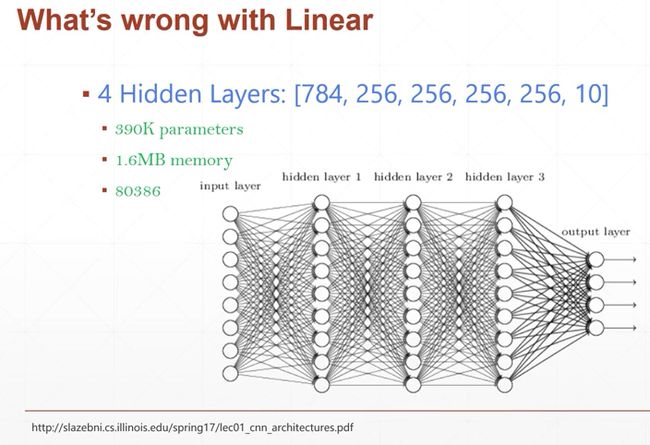
现在还有一个很小的问题就是,因为我们这里的每一个模型都是线性的,即使通过嵌套,增强了她的表达能力,但是他总体的模型还是线性模型,对于一个手写数字来说,比如说1,我们人之所以能够把它识别成1,是因为人脑有很强的表达非线性的能力。对于一个线性模型来说,它是很难完成手写数字体识别这种显示世界中的简单问题的。那怎么解决这个问题呢,我们在这里引入一个新的东西。我们在每一个函数之后,添加一个非线性的部分,这个非线性的部分它是怎么来的呢?

这个非线性的部分是源自于生物学当中的神经元。对于一个神经元,它有多个输入,然后它还有一个输出,这个输出呢,它不是一个简单的线性求和,它是有一个阈值,就比如说,当你的输入非常非常小的时候,它的输出可能就是0,而当你的输入非常非常大的时候,你的输出也不会非常非常大。
简而言之,就是通过你的输入来进行调控。这个就是一个非线性的函数。最常见的有sigmod函数和relu函数。

3.6手写数字识别体验

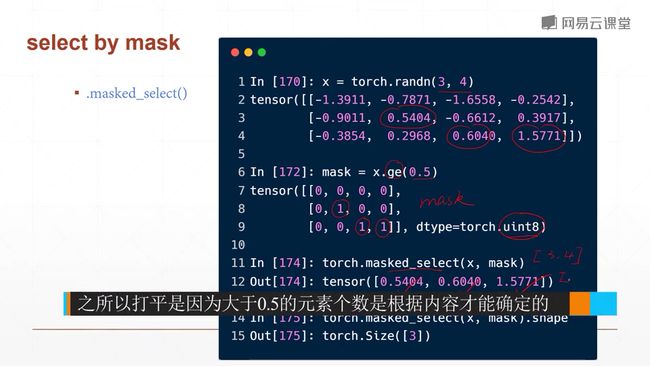
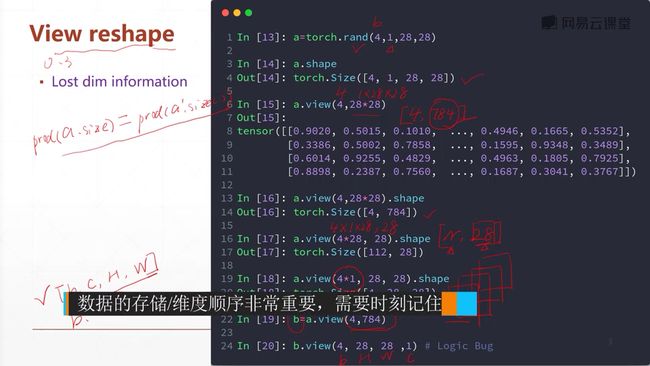
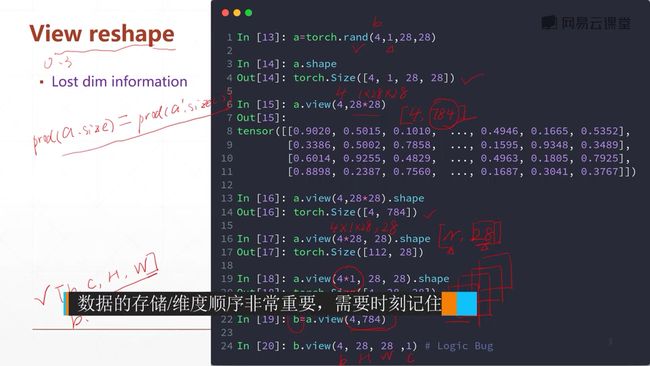
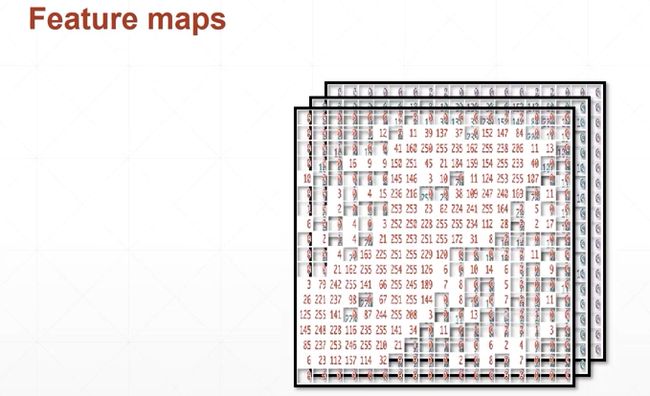
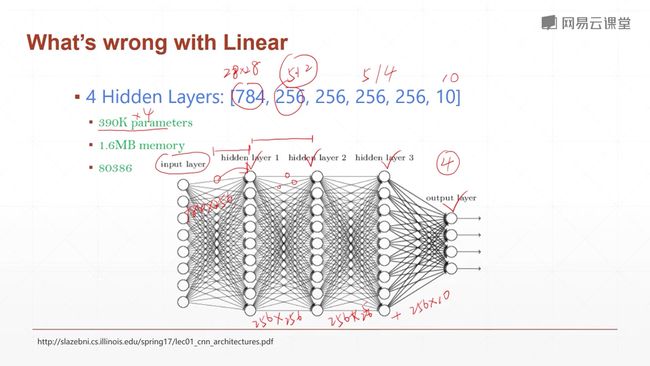
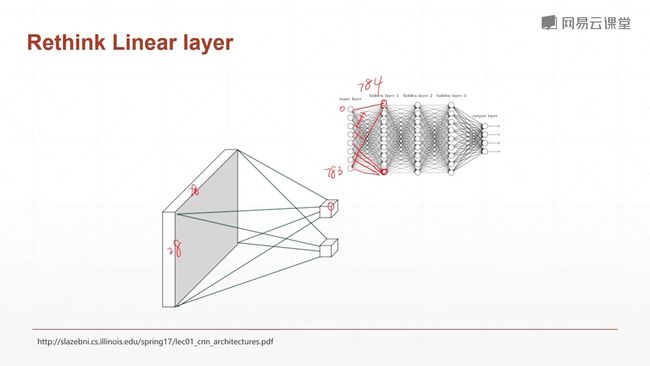
我们用28*28的矩阵来表示一个图,图中的每个元素我们用0~1来表示,这个值代表了这个点的灰度值,0表示白色,1表示黑色。或者相反也可以。然后我们将这个矩阵打平,由二维变成一维,但是数据量是不变的。这样子的好处就是,我们忽略了二维的位置关系。
但是对于这个问题,我们仅用一个线性函数是无法解决的,我们要使用三个线性函数的嵌套,首先我们来看第一个线性函数,
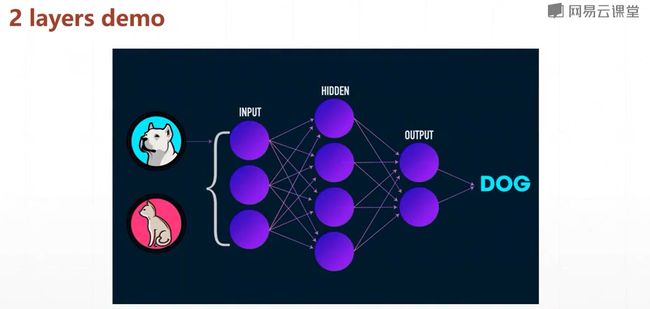

一般来讲,我们最后一层的网络的输出,它的一个激活函数,一般不会是relu,它会根据你的一个具体的任务来选择函数。

下节课,我会向大家讲解如何使用Pytorch来把我们这节课讲的这个理论部分变成实践。并且很好地预测mins数据集的number数字。
batchsize的概念? 因为GPU性能非常强大,一次可以处理多张图片,如果你一次只处理一张图片的话,你可能整个的传播过程大概是三毫秒,你一次处理十张或者100张图片,你占用的时间也就是4、5毫秒的样子,这样的话,通过并行处理图片,可以大大节省你的计算的时间。batch_size指的就是你一次处理的样本的数量,比如说图片的数量。比如说你一次处理的图片的数量。
4Pytorch基础
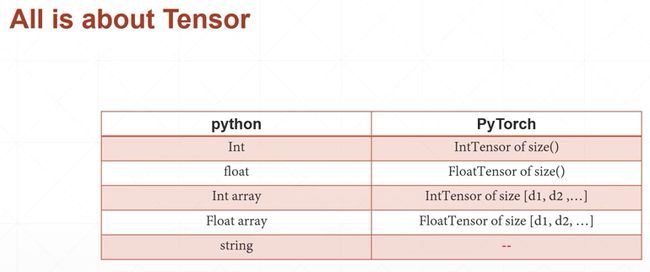
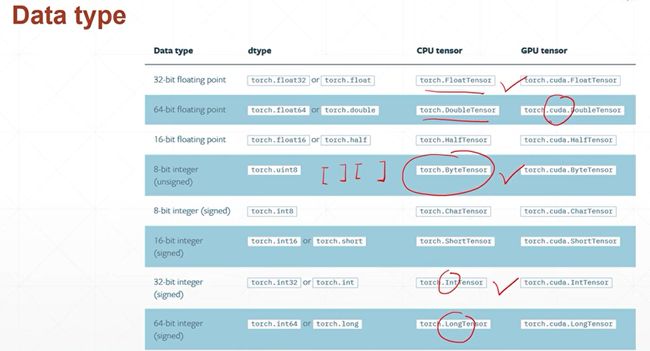
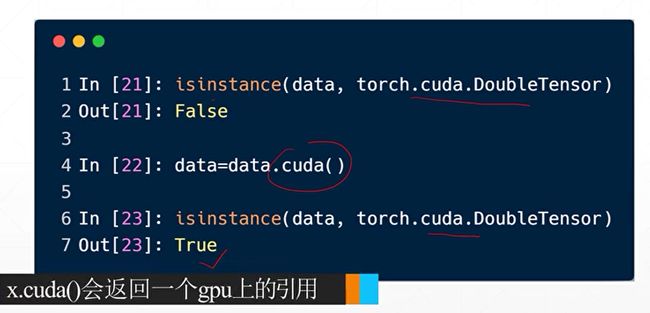
4.1张量数据类型
4.2创建Tensor
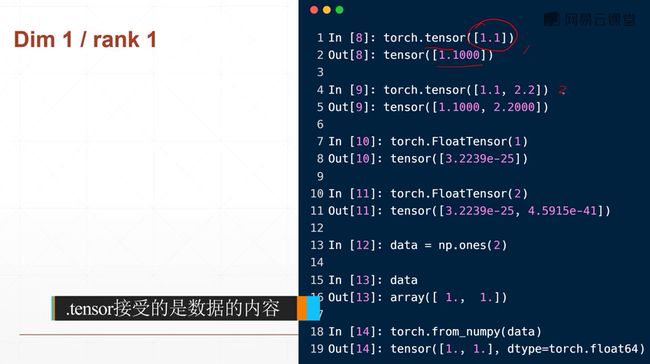
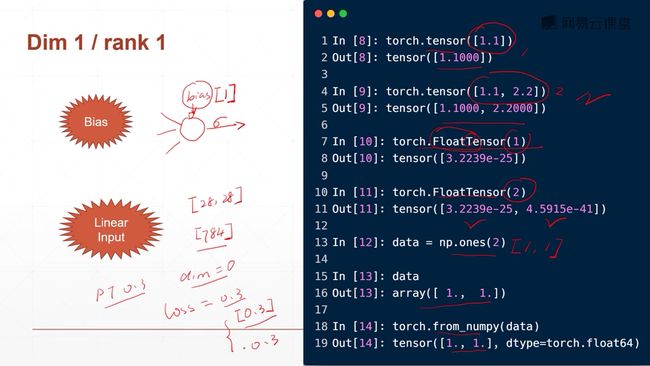
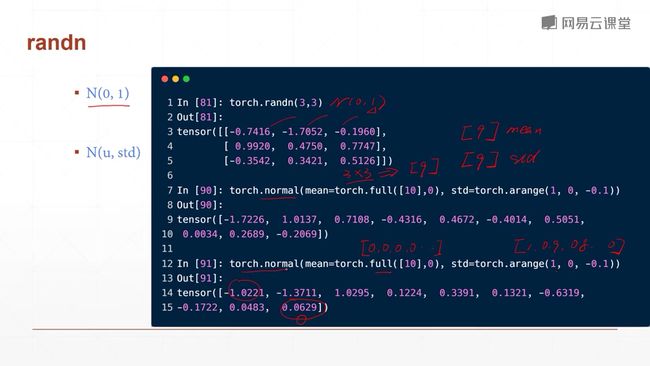
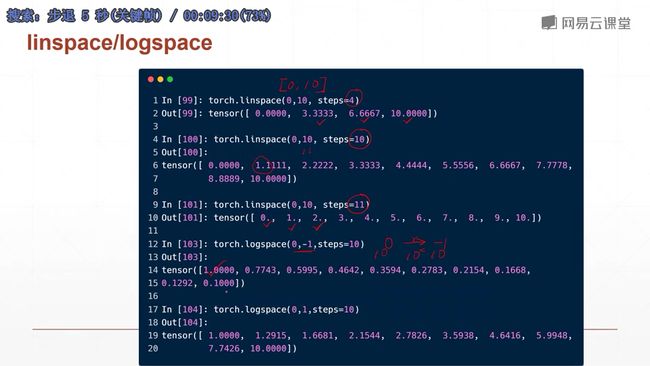
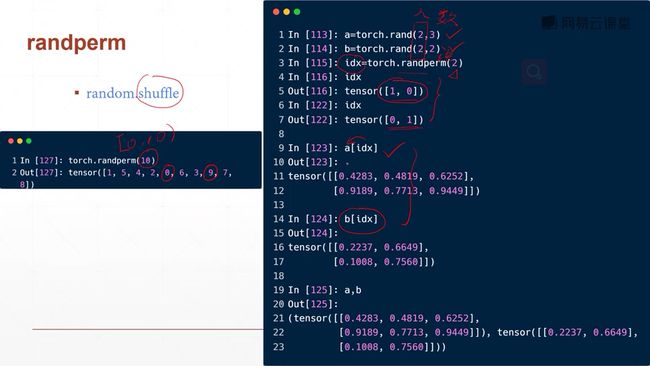
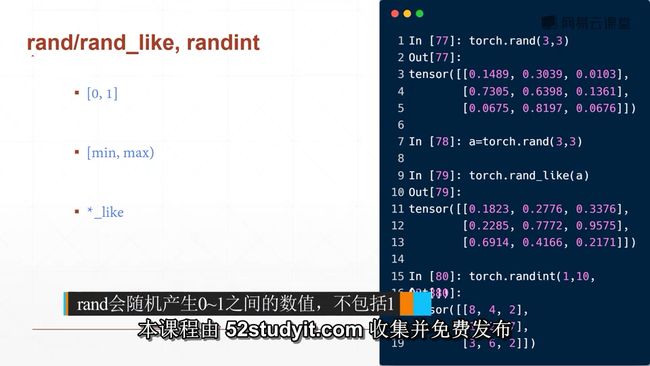
小写的tensor接受现有的数据(常用,尽量不要用大写的传现有数据,大写的传shape)
大写的Tensor接受的是数据的维度shape(也可接受数据,后面再讲)
torch.FloatTensor(d1,d2,d3)

如何申请未初始化数据的内存空间?注意直接使用这些内容空间时会有问题,因此初始化后作为容器一定要赋值使用



上面的没有初始化直接申请的空间会存在很多隐患,因此我们推荐使用随机初始化的tensor。
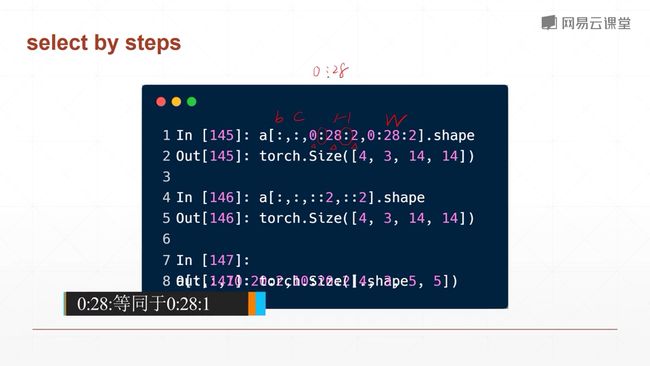
4.3 索引与切片
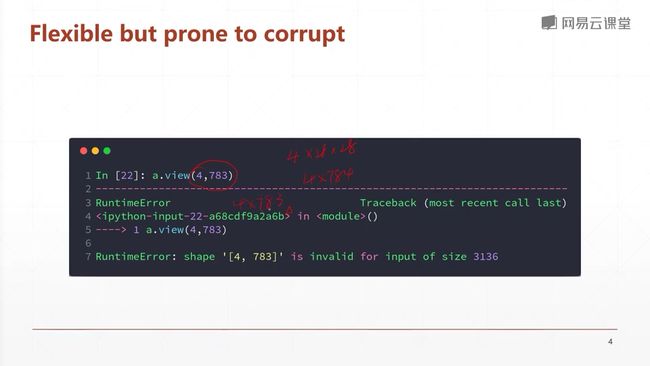
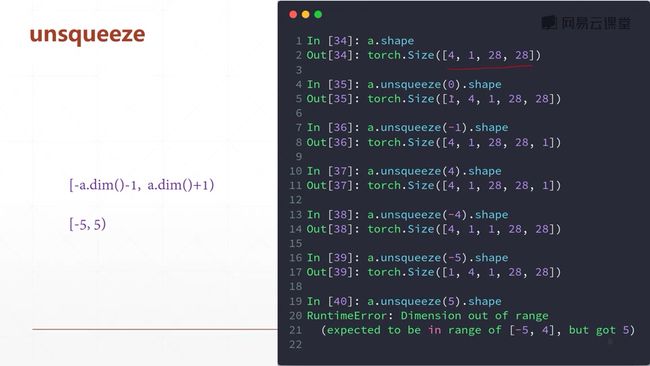
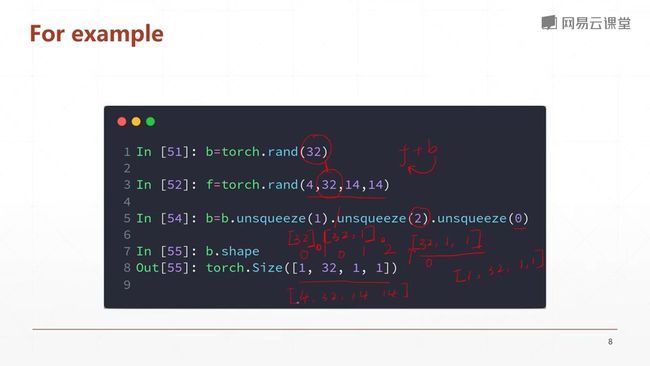
4.4 维度变换
5随机梯度下降
5.1什么是梯度?

导数,反应的是y的值随着x值的变化的变化率。
导数本身是一个标量,它反映的是某个方向上的变换快慢的程度。
在大学里,学到了更高维度的函数,因此有了偏微分。导数的方向是可以随便指定的。但是偏微分讲定的是给定的自变量的方向。有多少个自变量,就有多少个方向。
梯度:定义为所有偏微分的向量。
函数的梯度:就是把所有的偏微分看成一个向量来理解,所以梯度他是一个向量,它不是一个标量。这一点是有本质的区别的。
我们讲偏微分就是一种特殊的导数,它的方向是给定了的。也就是函数沿着x轴沿着y轴变化的一个趋势。它也是一个标量。而对于导数来说,他是一个非常通用的概念。它反映的是在给定一个方向上面的变化量。因此它也是一个标量。它只有大小,没有方向性。
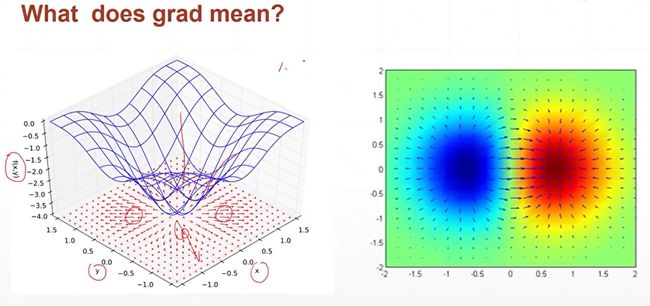
我们知道导数反应的是函数的变化量。那么梯度反应的是什么呢?
直观来看:
1、梯度的长度,反应函数的变化趋势,变化的快慢,越长越快,也可称之为速率
2、梯度的方向,代表它朝着它函数的值越来越大的方向走

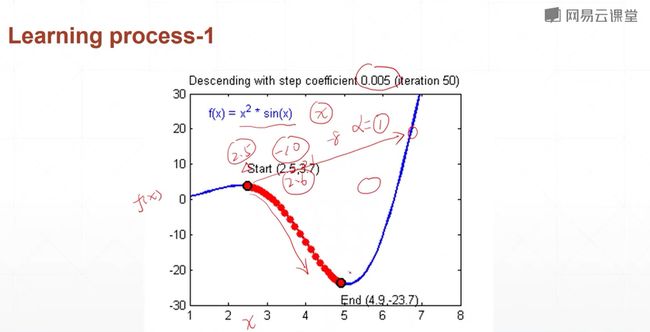
那如何利用梯度向量来搜索极小值解呢?一般情况我们是搜索极小值,如果你想搜索极大值的话,你可以把这个Loss变为负号,这样子你就可以通过搜索极小值解来帮助你找到一个极大值解,我们这里只讨论极小值。
最开始的值,我们通常都是随机初始化的。
5.2 什么是梯度
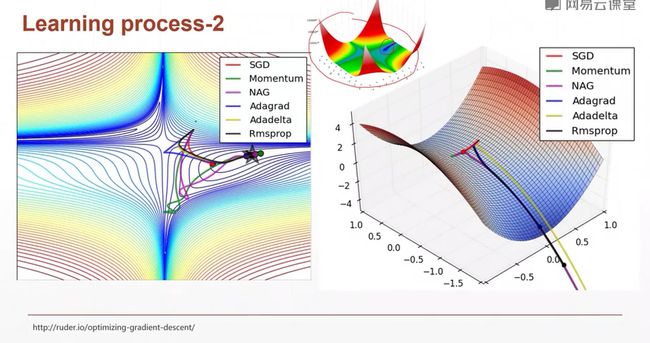
随机初始化为右上角的一个解,这里自变量是x,y,所以是一个二维的平面,每一条曲线代表的是一种不同的优化算法,对于某一个向量来说,它的梯度下降就是$\theta '= \theta - \alpha*\Delta_\theta$
左图下边的是局部最小值,左图右边的是全局最小值。
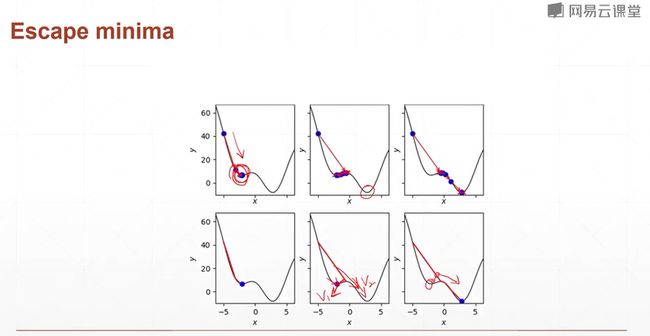
右边这个类似马鞍的图像,我们会发现,原始的SGD搜素卡在上面的位置了,我们后面会讲为什么会出现这种状况。因为你在搜索的时候,你只有目前的视野,所以,如果你没有其他的力量的话,你很有可能卡在一个局部的情况当中,动不了了。
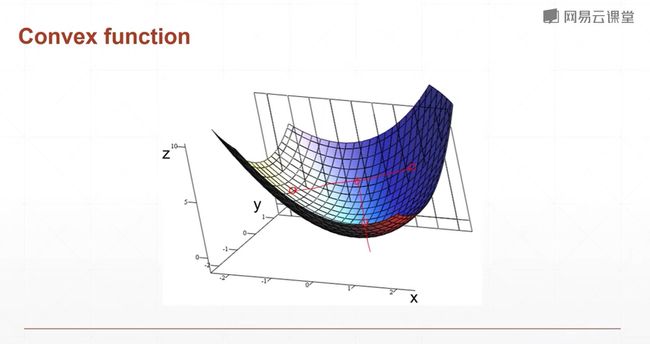
图形中,对于任何的两个点,我们拉一条直线,这条直线中间的中点,以及这个中点所对应的的函数的值。分别定义为z1和z2,对于这个图形始终有z1>z2,这个图形像网一样,这样的图像对应的函数是凸函数。对于这样的图形,总可以找到一个全局最优解。
局部极小值
凸优化在现实生活中存在,但是不太常见。下图是现实生活中存在但是不太常见的例子。
ResNet-56 由华人何凯佲发明
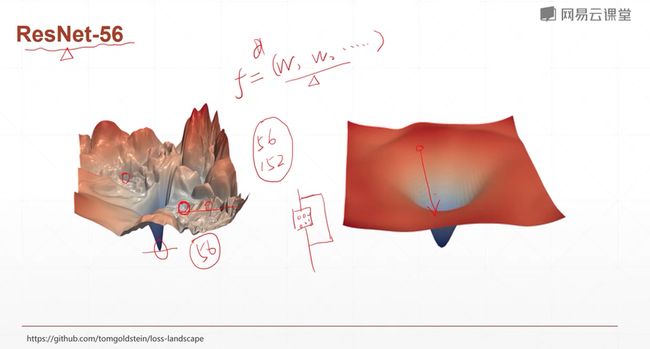
左图是56层神经网络的损失函数的图像,右图是引入resnet机制,加入通道后的网络,图像明显变平滑,优化速度变快。这也就解释了为什么网络可以叠加地很深而且可以很好地优化。
鞍点
鞍点:对于一个方向(平面)是局部极小值而对于另一个方向(平面)是局部极大值

因此对于x和y这两个维度的局部最小值和局部最大值的情况是不一样的。因此鞍点是比局部极小值更可怕的一种情况,因为通常我们的网络有上百的输入,w0,w1…参数有成百上千个,总会出现鞍点的情况。就是说你在这个自变量上取得一个极大值,你在另外一个自变量上取得一个极小值。
在鞍点就会卡住,导致搜不到全局最小值解。
影响搜索过程的其他因素
-
初试状态
如果你不知道如何初始化的话,你就按照凯明在paper中讲的,凯明的初始方法。
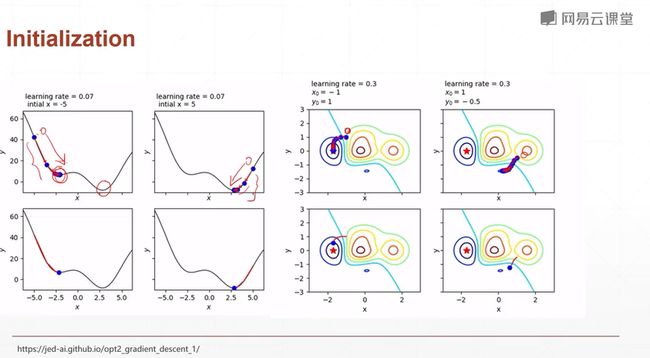
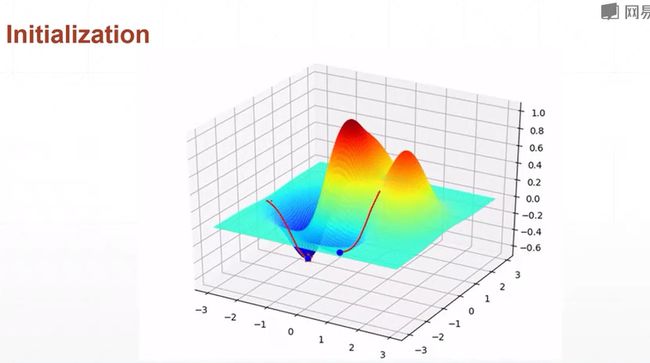
同样的网络,同样的参数,不同的初始化,往往会导致不同的结果。 -
学习率
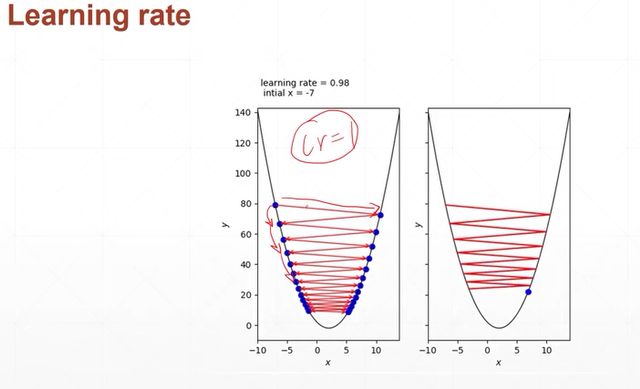
学习率最开始最好设置小一点,如果慢慢收敛了,你再试着把学习率增大一点,这样收敛地更快,但是如果你一开始就把学习率设置地很大的话,函数很有可能不收敛。
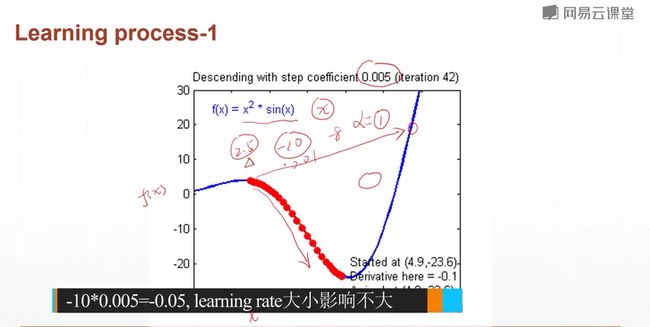
learnning rate即影响速度又影响精度。
5.3 常见函数的梯度

在高中和大学,会陆陆续续学习一些,函数的梯度求解方法,我们这里将梯度和导数的概念混在一起讲,是因为导数是给定的方向,而梯度是所有方向上面的一个综合。
对于一个一维函数,它只有一个方向,因此一维函数的梯度和导数基本上就是一个东西,只不过导数是没有方向的,而梯度是有方向的。
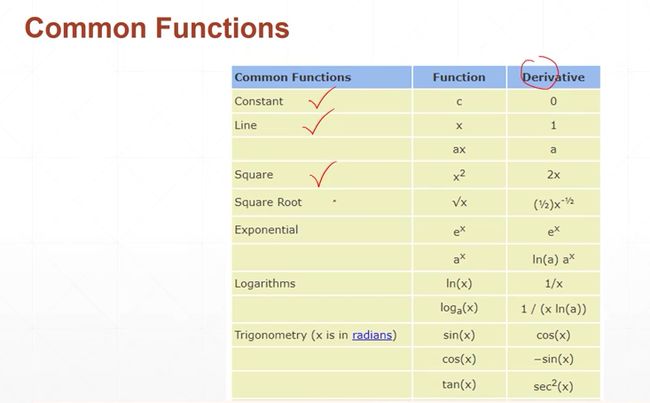
w作为神经网络的参数,x作为神经网络的输入,b也是参数。
w,b是我们整个神经网络要优化的目标。w,b看成是两个自变量。x是参数。
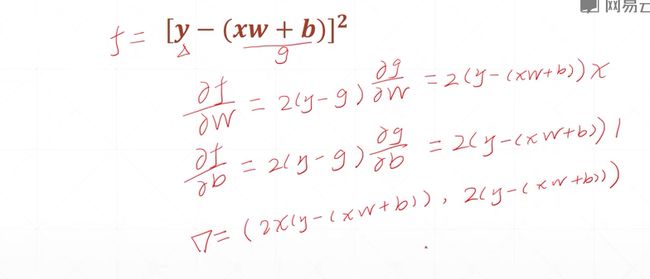
这个式子稍微复杂一点,但是这个式子就是我们真真实实的单层感知机在使用均方差的一个loss度量的一个导数,或者说是一个梯度。因此我们对于一个单层的感知机,使用均方差的时候,它的梯度是可以直接使用closs found直接计算出来的,我们可以直接使用我们计算出的梯度信息,对任何的w和b的状态,求解出该状态下对应的梯度,然后直接进行更新就可以了。这个式子对于我们求解一个单层的感知机来说是非常非常方便的。
激活函数与loss梯度1
由于它不连续,不可导,因此我们必须对他进行优化,从而让激活函数可以进行梯度下降。
为了解决单层感知机不可导的问题,科学家提出了一个连续光滑的函数,名字叫做sigmoid或者叫做Logistic 就是逻辑回归。
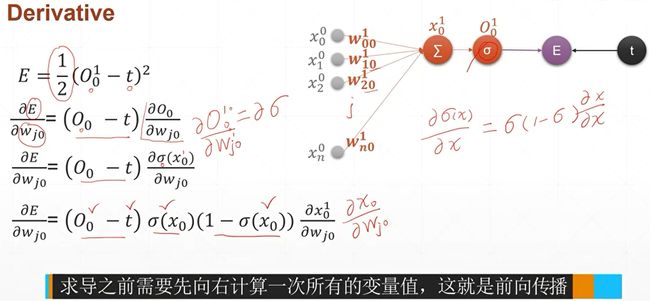
因为 sigma 使我们神经网络当中的一部分,我们在做前向的时候,这个sigma的值等于多少是已知的,因此sigma这个值对w的导数等于sigma乘以1-sigema。因此这个导数也是已知的。
所以说它求导的过程中是非常非常简单的。需要再额外地再去求导。你只要根据它现有的值相乘一下就能够求出导数。
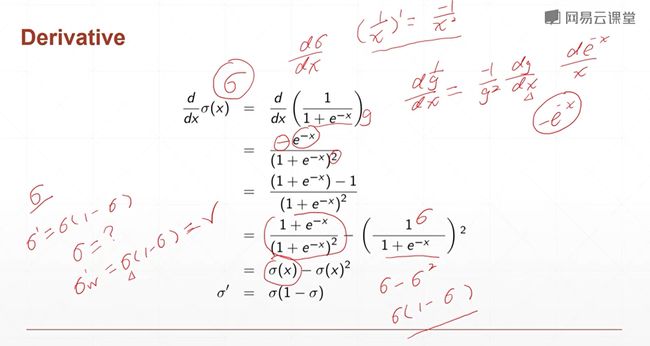
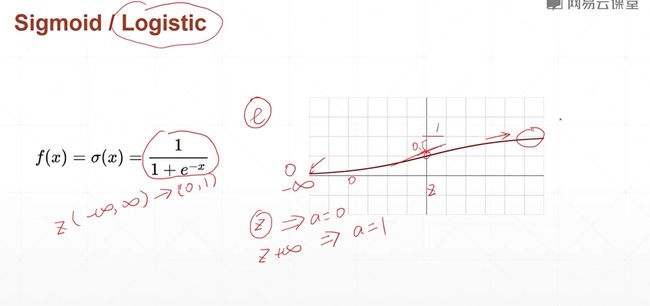
但是呢,当x特别大的时候呢?梯度=0,就会导致梯度长时间得不到更新,就会出现梯度弥散。
激活函数tanH 在RNN中用的比较多!
sigmoid Y轴放大两倍,X轴缩小两倍,再平移2.

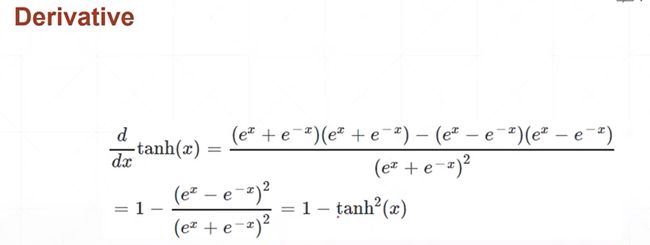
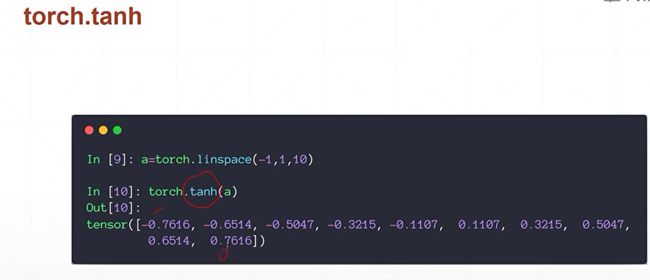
整型线性单元 RelU, 神经网络的奠基之作
减少梯度弥散的出现,右侧部分的梯度永远是1,它在做向后传播的时候,因为你的梯度信息是1,导致你这个梯度计算起来非常非常方便,不会放大也不会缩小,因此对于搜索最优解,relu函数具有先天的优势。它的导数计算起来非常的简单,而且由于其梯度不变性,也不会出现梯度弥散和梯度爆炸的情况。
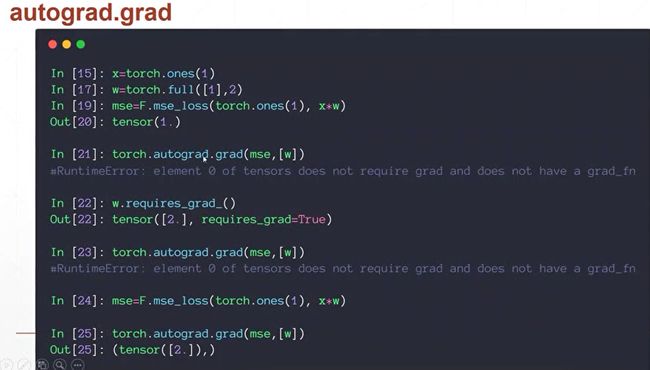
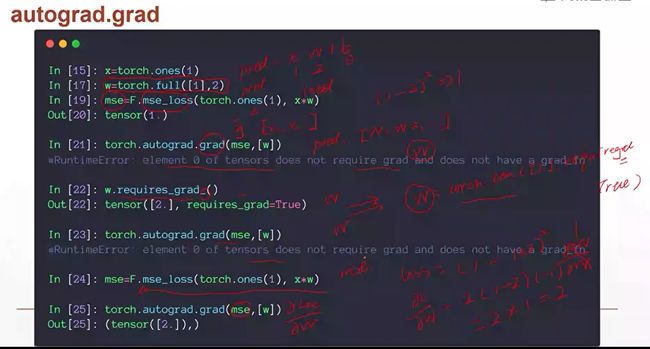
激活函数与Loss梯度2
p = F.softmax(a,dim=0),这个建图过程会自动完成一个前向的操作。
每调用一次backward,就会进行一次反向传播,计算梯度,并把梯度信息放到成员变量w.grad内,并且把这个图的梯度信息给清除掉。因此当你第二次使用backword来操作的时候,就会报这个错误,他会提示你让你设置标志,p.backword(return_graph=True),当你调用这句话,除了会得到你的梯度信息以外,他这个图是不会被清除的。因此你可以再次使用P.backword来获得t度信息。但是如果你在第二次Backword的时候没有设置这个标志,那么第三次backward就不行了。这个标志只会保持一次。因此我们这里本来已经写了这句话了,会因为你没有设置这个标志,当你再次使用的时候这个图就被清掉了,你就不能再次backward了。
然后下面需要注意啊,我们这里无论是使用grad函数,还是使用backword函数,我们最终要的这个loss,一定是一个维度为1长度为1的东西,或者说是维度为0的这样一个scale。就比如说你的Loss是一个长度为1,feature为3的时候,它是不可行的。你的Loss是必须只有一个量,不能有3个量,当你有3个量的时候,说明你的代码一定是有问题的。你的逻辑是有问题的。
我们来看一下,我们这里的P是,是长度为1,维度为3的这样一个vector向量,因此我们在求导的时候,不能够直接传P,因为P不是一个长度为1,维度为1的,我们只能对p中的第二个,或者是第三个(下标为2)进行一个求导,因此我们这里对P的第二个变量也就是
6.5 感知机的梯度推导-1
从这一节课开始,我们会带大家领略一个完整的多层神经网络梯度推导的过程。

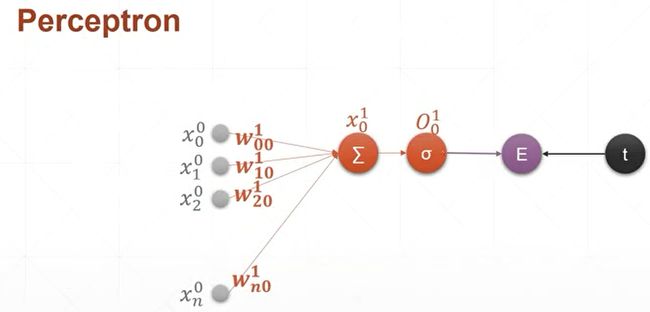
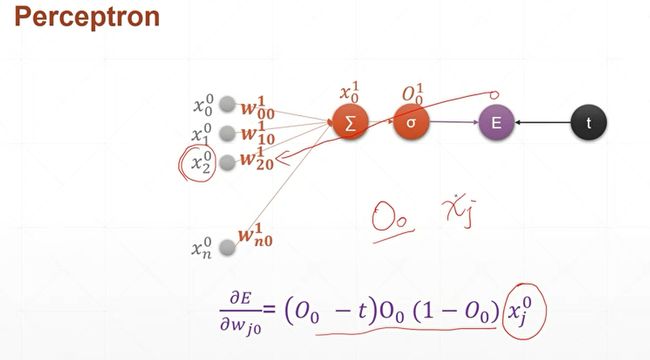
首先我们来看一个,单层的感知机的梯度的计算,以及它的梯度更新的这样一个过程。首先我们来回顾一下,单层的感知机模型。单层感知机,每一个输入节点xi和他对应的权值wi节点,相乘累加以后,再跟一个bios相加,得到的就是它的预测值,下面是它的数学模型,我们已经见过了,因此我们不讲。
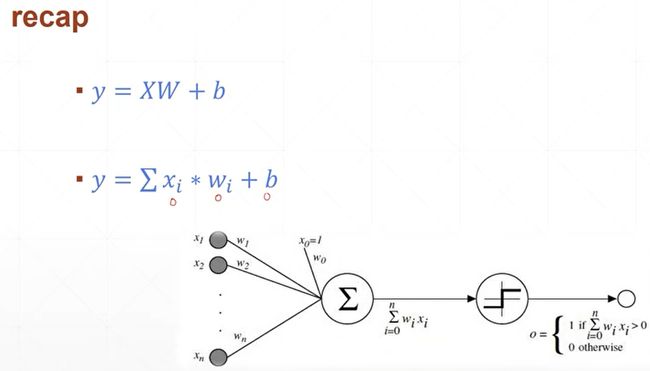
现在我们来看一下,对于单层的感知机,
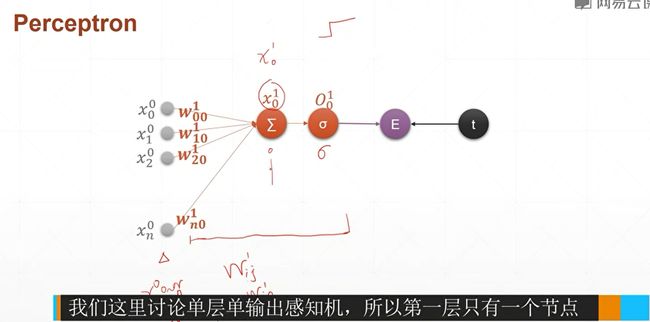
对于单层的感知机,我们已经见过了,因此我们不讲。对于单层的感知机,我们前面讲过,它的激活函数是一个像楼梯一样的函数(不奇函数),这个函数是不可导的,我们在这里使用一个现代化的单层感知机的模型,也就是说它的激活函数不再是一个步进的模型,而是一个sigmoid函数,也就是sigma希腊字符来表示sgimoid函数,现在我们来对符号的定义来进行一个规范化,首先是,对于输入层,我们把每一层进行一个编号,比如说,对于这个输入层,它的层数是第0层,因此对于输入层上面所有的元素,我们的上标0,表示它是属于输入层的,它的下标0~n,表示第0层,一共有n个元素节点。输入,求和以及激活函数sigmoid的输出我们称之为一层,每一层中的参数包括权值w,权值的上标1表示第一层,也就是第一个隐藏层,同时它有两个下标,第一个下标i表示的是连接的上一层的xi结点,第二个下标j表示的是连接的是这一层的j号结点,也就是说,表示上一层的i和这一层的j相连接。因为我们这一层中间层只有一个节点,所以j总是等于0。因此我们这里的wi0,就表示上一层的i号结点与这一层的第0号结点,因为我们这里只有一个节点,然后他的上标1就表示这一层的编号,也就是第一个hidden layer,然后,我们把加权求和的变量起了一个名字,叫做x1下标0,x1表示是第一层上面的x,x下标0表示第一层上面的0号结点,然后,对于x1下标0,它经过激活函数以后会得到一个输出值,我们把经过激活函数的这个输出值起个名字叫做O,O1下标0,1表示第一层,0表示第0号结点,我们这里需要注意的是,因为我们这里仅仅推导了一个单层的感知机,也就是说,第一层只有一个节点,
 ,就是上图这个节点。
,就是上图这个节点。
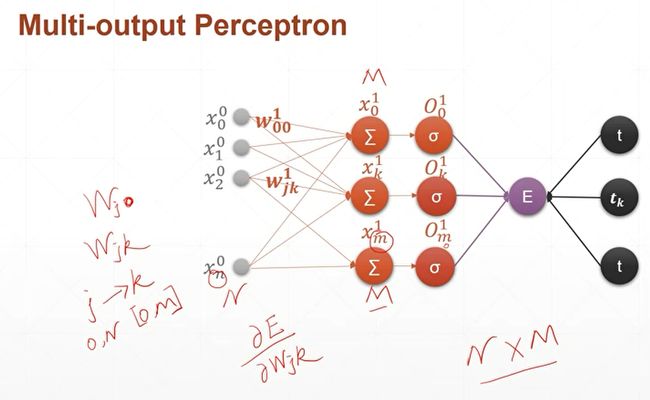
然后,对于我们后续还要推导的多层的感知机,也就是层数有多层,每一层上的结点数量也有多个,因此它可能存在x1下标1,x1下标2,这样的结点。

然后对于每一个x,它的输出,也就是经过激活函数以后,它的编号变成了o1下标1,o1下标2,o^1下标3,为了跟后面的编号保持一致,我们这里还有一些,重复的累赘,比如说这里0号结点我们也写出下标0来啦,这是为了后边方便我们很快地类推到多个输出节点,以及多层上面的一个编号,同样的我们这里的w20也保留了这样一个0的编号。


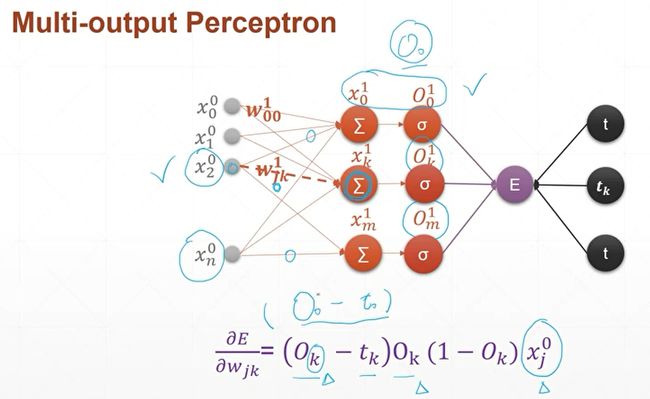
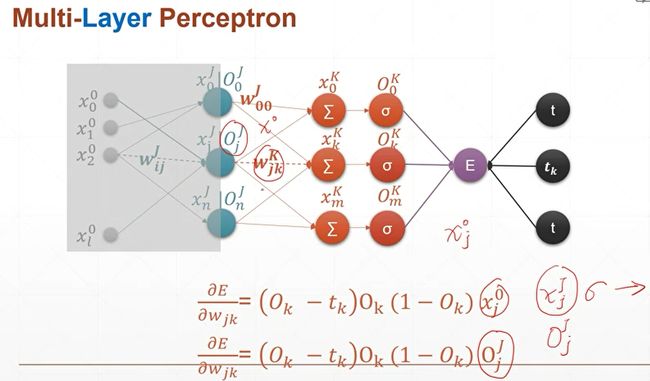
然后经过激活函数以后,O10跟他的target的值做一个Error或者一个loss,就是(O1下标0-t)2,因为只有一个节点,所以求和符号可以省略。现在我们已经把命名规则和大家讲清楚了,对于任意的符号,比如说X,上标表示层的编号,下标表示当前层节点的编号。对于权值来说上标L表示层数,下标i表示上一层节点的编号,下标j表示该层节点的编号。
在这个编号的前提下,我们来推导一下单层感知机的梯度的推导公式,首先我们来写出单层感知机的输出的误差的计算公式,我们把输出的值和它的目标值做一个平方和。这里引入了一个额外的1/2,这个参数是为了跟后面的求导的2抵消掉,如果你写不写1/2都是一样的。因为它的梯度的单调性是不会改变的。下面我们进行一步步的推导。
输入是一个x节点,有十个feature。跟一个一维且有十个w权值做一个转置运算。
然后计算一个Loss,loss是一个标量,也可以理解成它是一个长度是1维的标量向量。

通过梯度下降的反复计算,就可以求得一个越来越优化的w权值。最终我们会得到一个相对较好的w权值,使得x*w的值越来越接近于趋近于它真实的y的值。这样就完成了一次梯度计算的过程。
本节课,我们通过手把手地推导一个单层的感知机的梯度,跟使用单层感知机的梯度,来更新,达到一个优化感知机的这样一个目的。
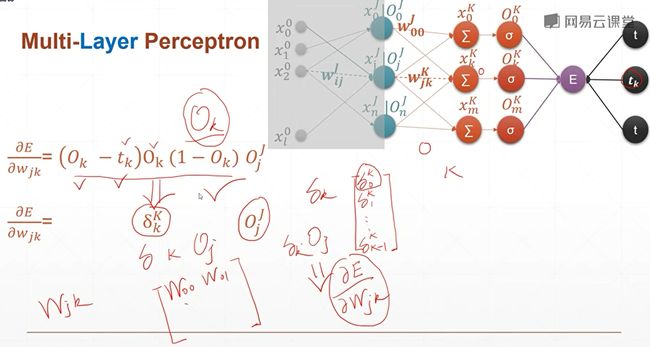
6.6 感知机的梯度推导-2
推导多层感知机梯度传导以及优化的过程。
6.7 链式法则
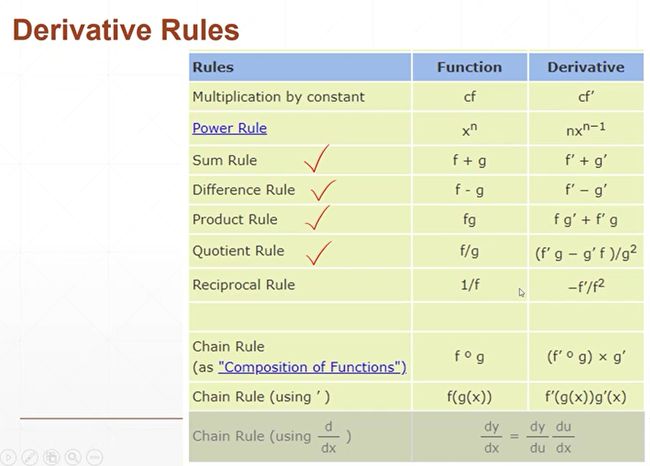
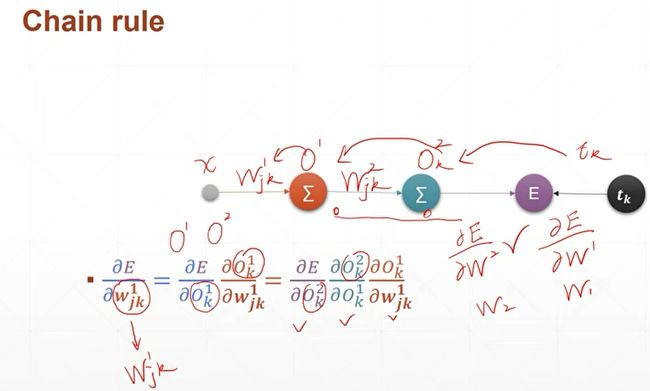
通过链式法则,我们就可以把最后一层的误差一层一层地输出到中间层的权值上面去,从而得到中间层的一个梯度信息。通过这个梯度信息,我们就可以很好地更新这个权值,从而达到一个最优化的效果。说到链式法则,我们前面的一些梯度推导过程中间其实不经意的就已经使用到了这一项法则,但是我们没有明说,在此我们正式地给它介绍一下。在介绍链式法则之前,我们来介绍一下一些其他的常用的公式。
包括:两个梯度的和、差、乘积、商、还有分子。
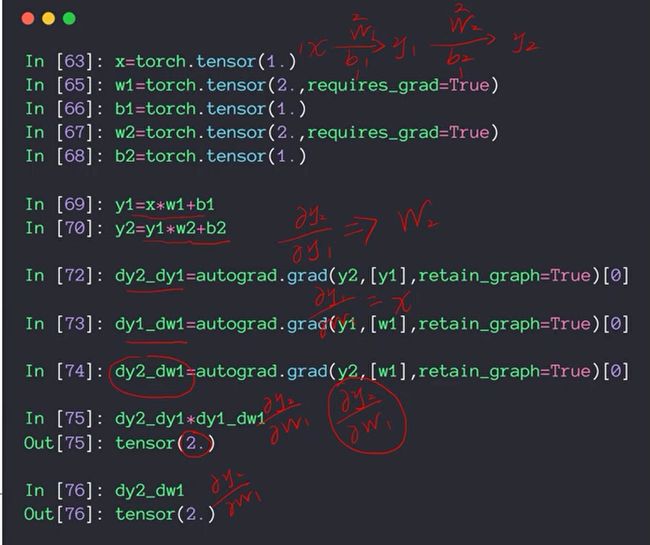
下面我们通过Pytorch提供的自动求导功能来验证一下链式法则。
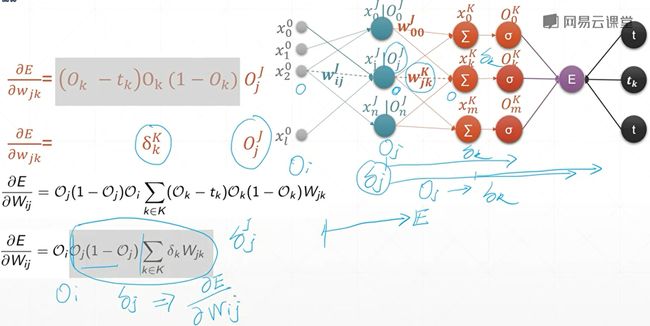
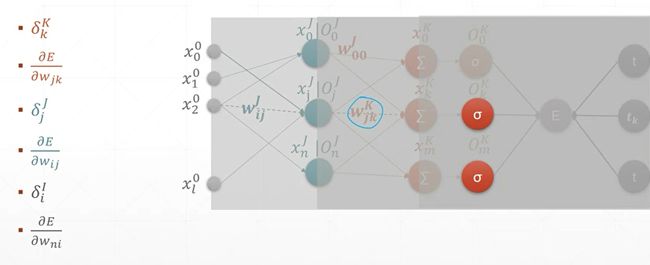
6.8 MLP反向传播
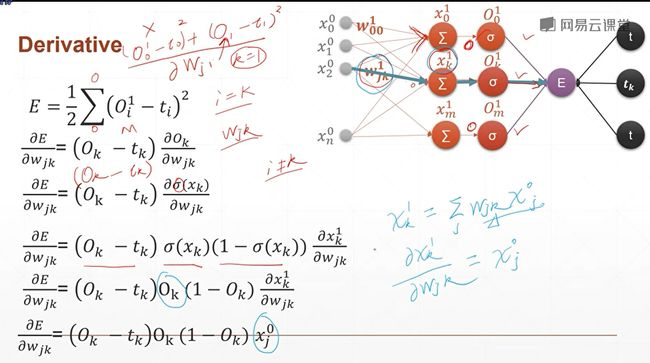
本节课我们将会介绍一个完完整整的,与我们实际使用一摸一样的,多层感知机的反向传播方式。本节课的公式稍微来说比较多一些,但是大家不要害怕,因为这将是deeplearning最后的工序。如果你对这个掌握了以后,后面的一些东西你掌握起来就会非常非常快。
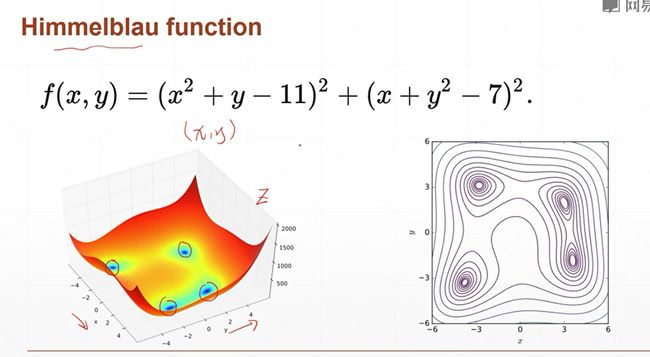
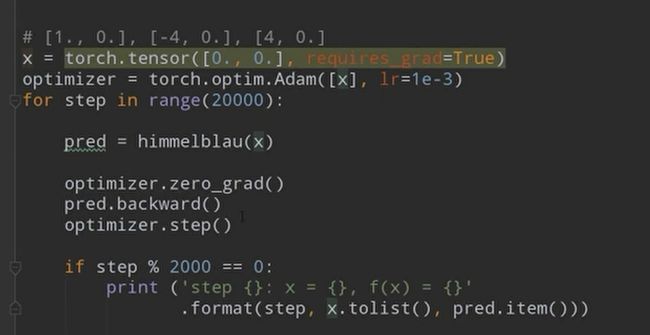
6.9 2D函数优化问题
这个函数有一个专门的名字,它是科学家用来专门检测优化器的一个效果,也就是说我们科学家找到了一系列的非常复杂的,或者说非常便于可视化的这样一些函数。通过在这些示例函数上来搜索和检测你这个优化器能不能找到一个比较好的解。像这个函数来说,它虽然有四个局部极小值,但是每一个值的解都是0,所以来说这四个解,其实都是权值最小解。因为它的解都是一样大的。
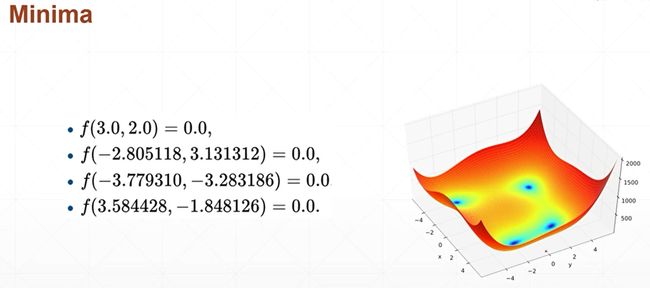
因此我们可以通过求解这个函数,来看一下我们设计的优化器,或者说我们设计的这个梯度下降法则能不能很好地找到这个解,因为这个解我们可以直接通过closed found方法求解出来了。我们只需要看我们通过mechine learnning方法求解出来的这个解跟我们真实的这个解的差距大不大,就知道我们这个优化器有没有真正找到比较好的最小值解。

7 神经网络与全连接层
9卷积神经网络CNN
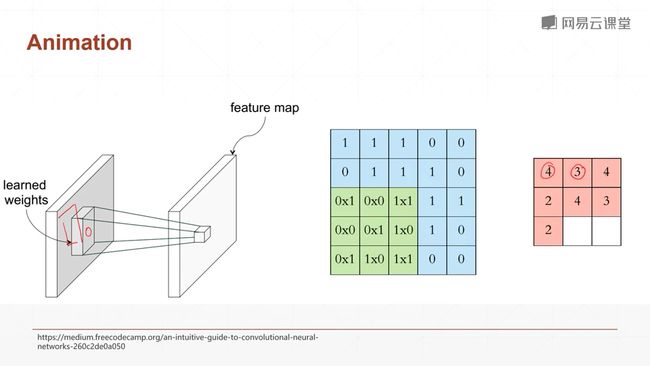
9.1什么是卷积?
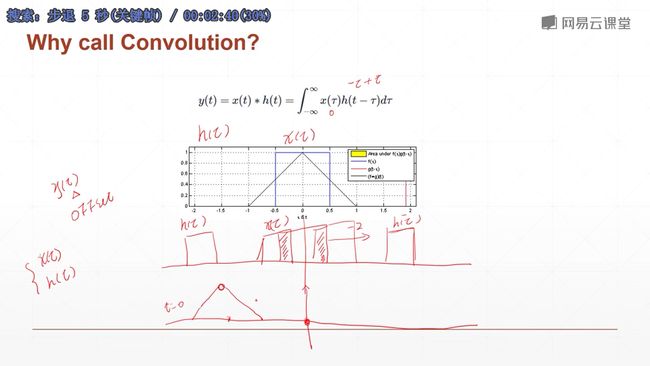
卷积名字的由来:因为它模拟的操作和我们信号模拟中的卷积运算操作是一样的,故得此名。
![]()
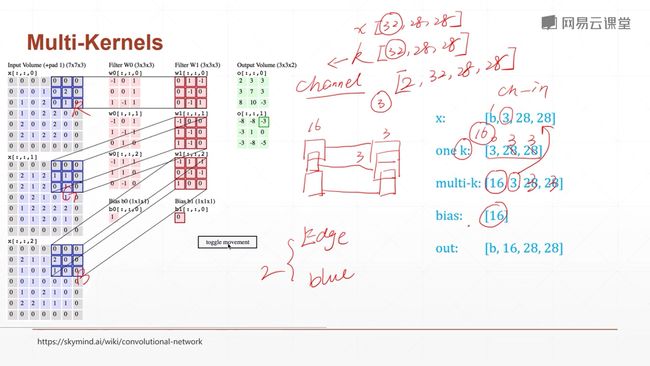
9.2 卷积神经网络
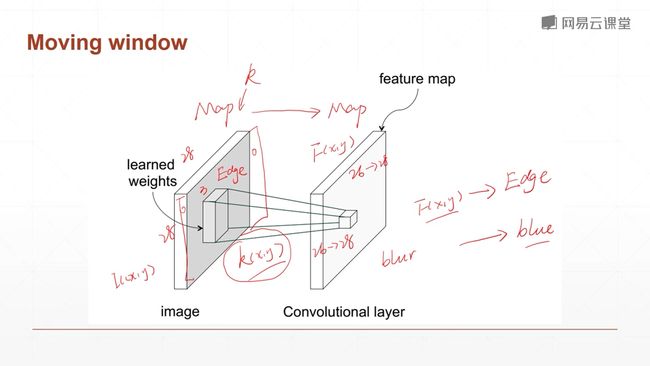
一个kernel(核)一个观察的角度,多个就有多个观察的角度。

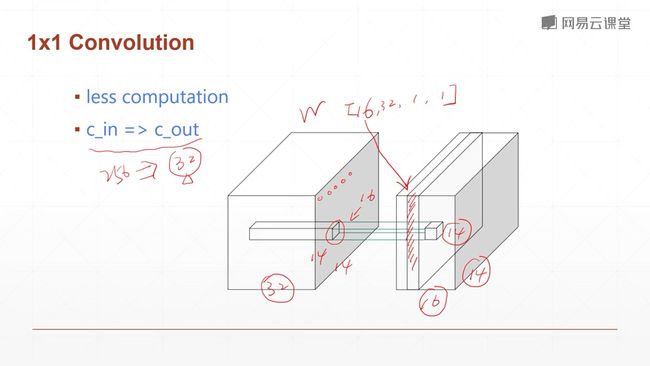
Input_channels指的是输入图像有多少个通道
Kernel_channels指的是你有多少个核(另一个意思 下节课讲解:就是说kernel还有一个通道数的参数,与输入的通道数相同,用于对输入图片的每一个通道进行特征提取)
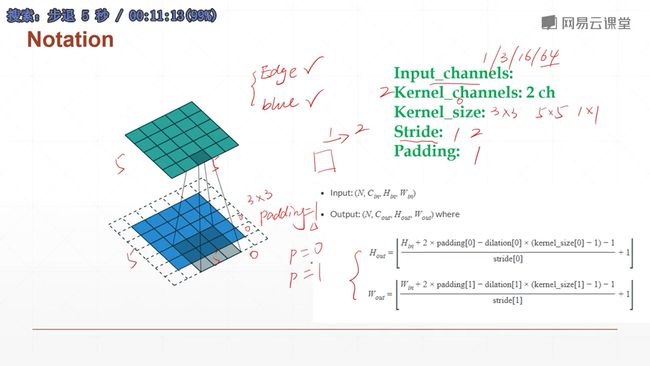
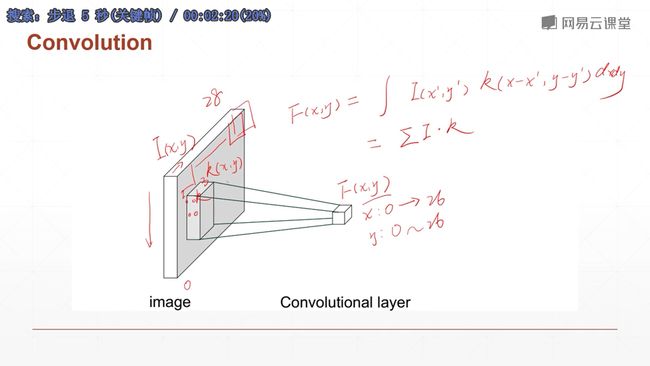
上图就是计算过程卷积后的结果层的H和W的Size的计算方法:
(输入尺度-+2*padding-kernel_size)÷stride下取整后-1
kernel的通道数= 输入图像的通道数
[2,3,3,3]
第一个channels指的是有多少个kernel,第二个channels与输入的通道数相同。
另外,每一个kernel都会带一个偏置,它与kernel的数量一致。
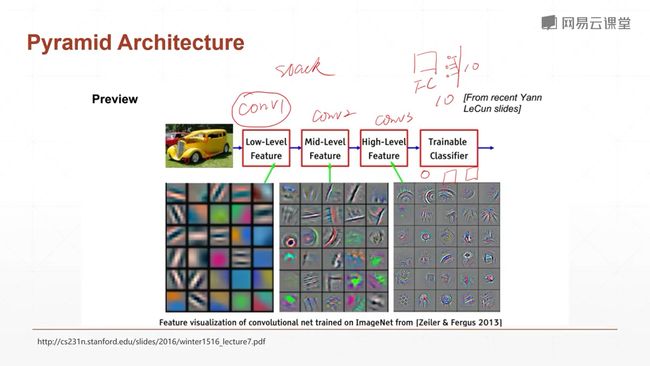
第一个卷积层kernel通常观测的是一些低纬度的特征,比如说下面这个车的菱形啊,角度啊,边缘啊,变化之类的。
而中间层的这些kernel呢,观察的是一些小维度的概念,比如说车的圆形等。
更高维度的卷积层提取的就是车的更高级的特征,比如说有没有玻璃、有没有轮子、有没有车玻璃等等。这些更高纬度的概念。
(以人脸为例,前免得卷积层观察轮廓、中间的卷积层观察肤色等等,再往下观察眼睛,鼻子等等。最红神经网络就根据这些高纬度的特征来进判断和分类。 这就是特征学习,它就是一个特征不断提取的这样一个过程。
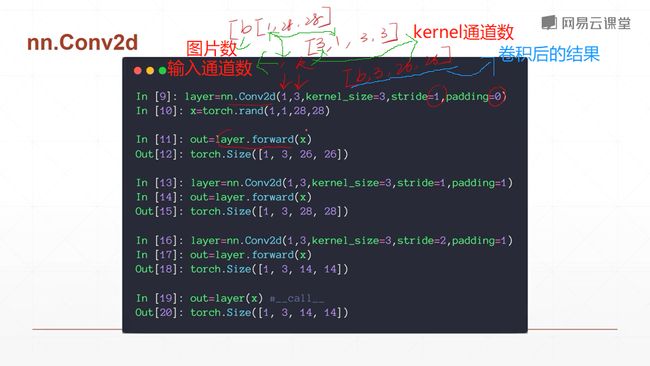
注意,用layer.forward函数可以完成前向计算。 但是pytorch有包装在里面,它推荐使用类的实例加过括号的方式进行调用,它调用的是内置的call函数,而pytorch在里面封装了hooks,这些hooks是高阶的特性,如果你要使用这些hooks方法,要类的实例调用。因此除非你十分清楚你要干什么,否则不推荐使用layer.forward这种计算方式。使用layer()会先运行hooks再运行.forward函数,它不但能够完成你的目的,还能够完成pytorch自带的一些功能建设。
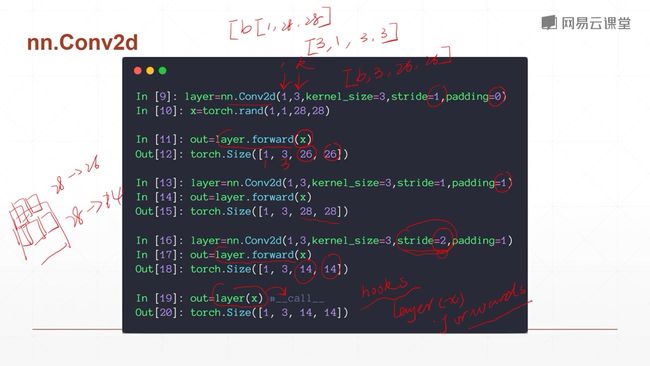
到这里,我们已经讲解了一层卷积是如何运算的,以及其中的input dimension 和 kernels dimesion的定义。根据kernels 的数量会得到我们一个output channels的数量。
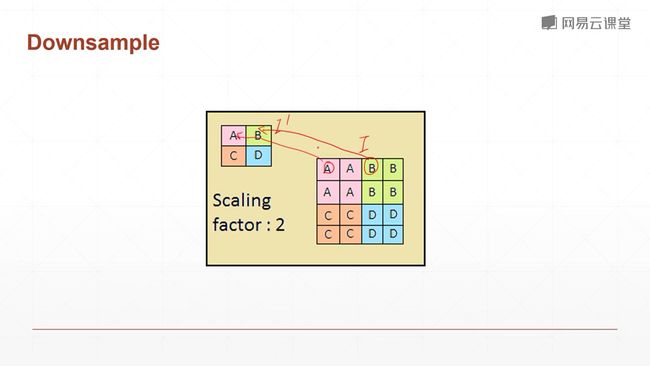
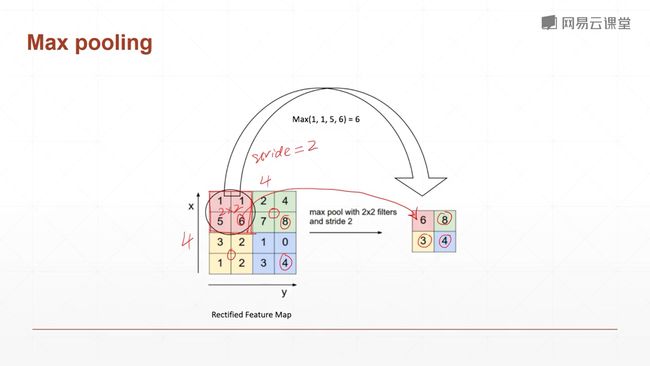
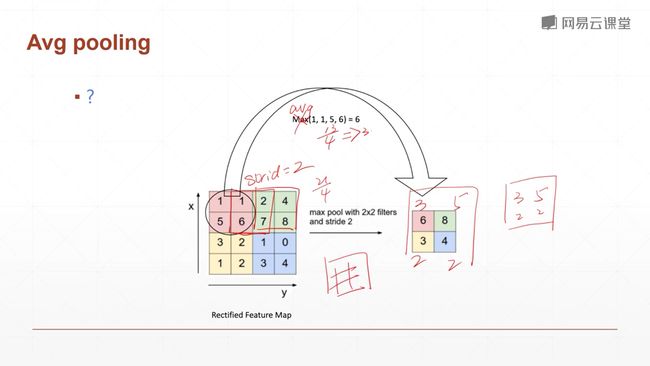
9.3 池化层
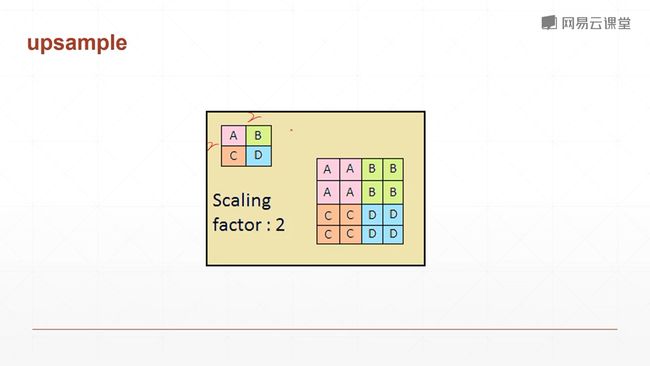
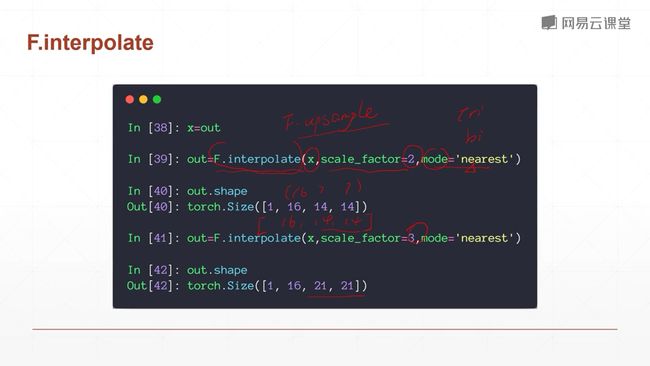
pooling层:下采样层,是一个把feature map变小的一个操作,和图片缩小不太类似
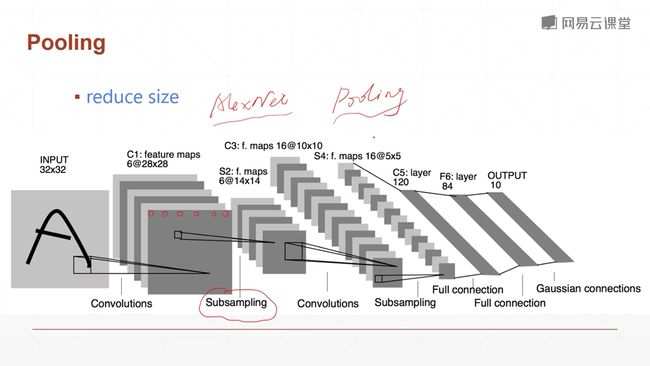
在LeNet中,不是使用pooling,而是使用subsampling隔行采样来降低数据量,降维,到了AlexNet我们就开始使用pooling滑动窗口了。
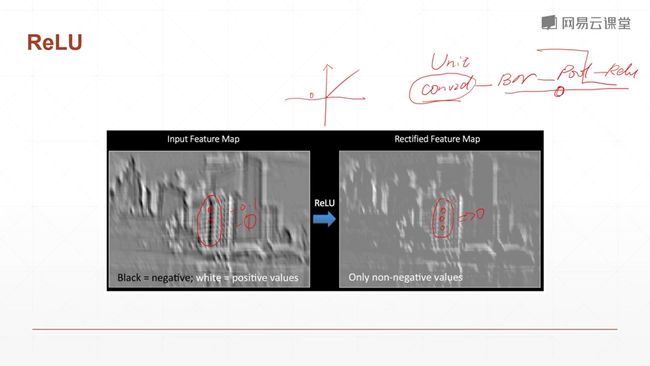
Relu函数,去掉负的响应低的函数。
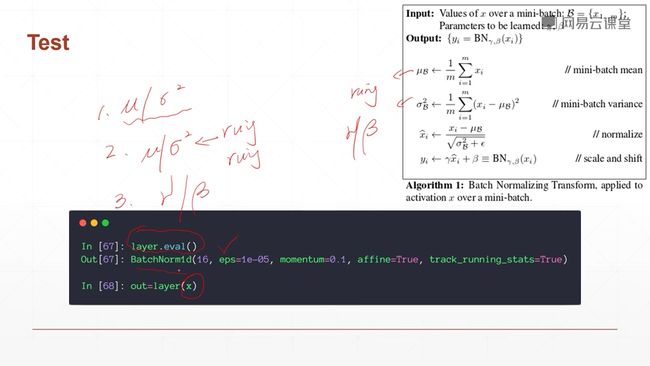
9.4 Batch Norm
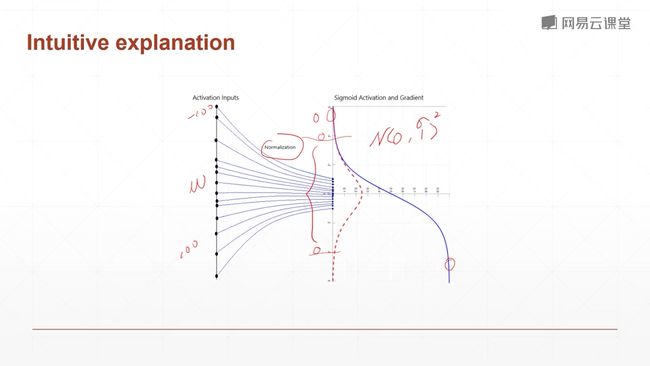
在sigmoid函数中,如果值超过-4或者4,就会导致导数为0,就会出现梯度弥散的情况,就是你的梯度会在很长时间内得不到更新,这并不是我们所希望的,我们会避免使用sigmoid函数,而会使用relu函数,因为relu函数不会出现这问题。但是,在有些场合必须使用sigmoid,因此我们希望把你输入的值控制在有效的范围之内。
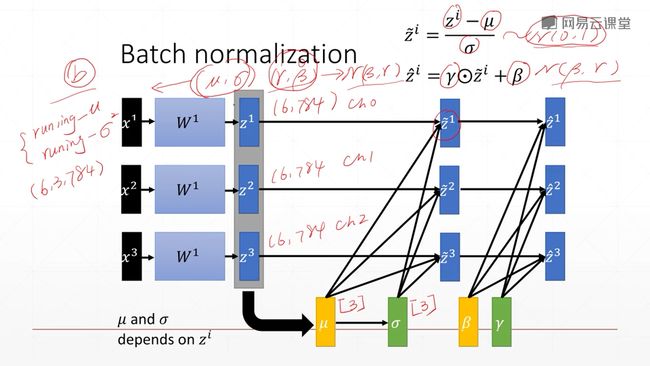
Test时,1取的是全局的$\mu 和 \sigma^2 $。
优势:
1收敛速度更快
2更好的最优解
3更稳定
9.5 经典卷积神经网络(LeNet5、AlexNet、VGG、GoogleNet)
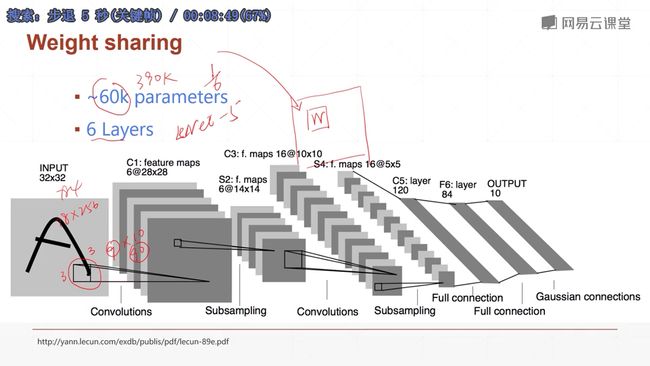
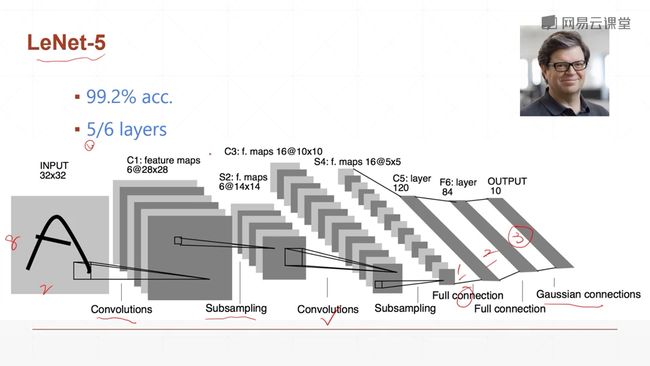
9.5.1 LeNet-5(80年代)
最开始是用于手写数字识别
,386的年代。那时候深度学习还没有很大的热潮。
一个卷积层、一个下采样,当时用的是隔行采样,又一个卷积层,然后隔行采样,最后是三个打平之后使用的线性层。
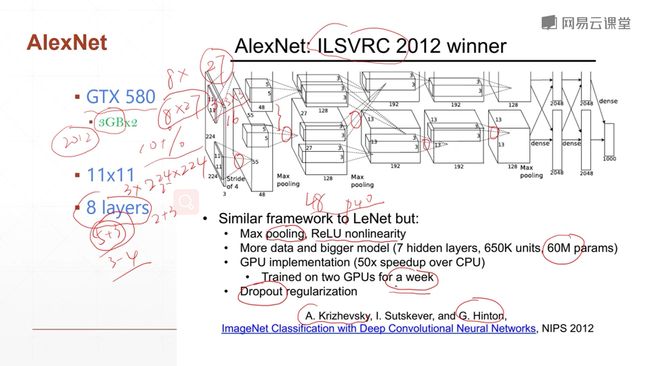
9.5.2 AlexNet
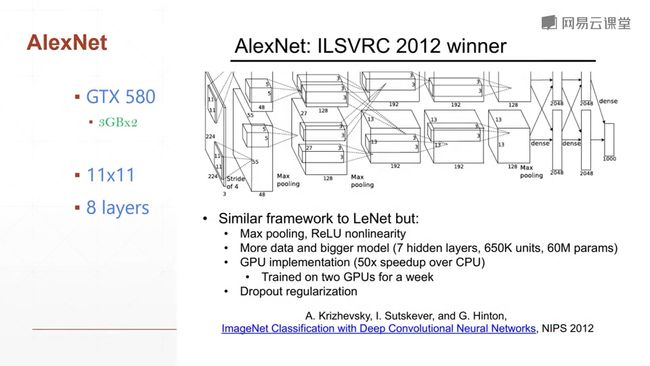
对于AlexNet我们学习的是它对于当时的一个影响力,而不是它的结构,因为它的结构是当时的比较中间的一个做法,由于当时显卡内存的限制。
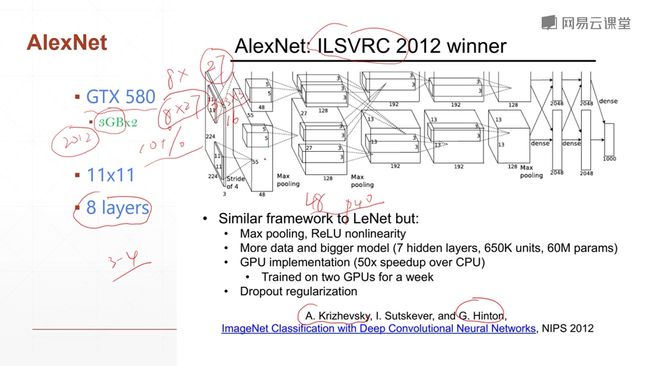
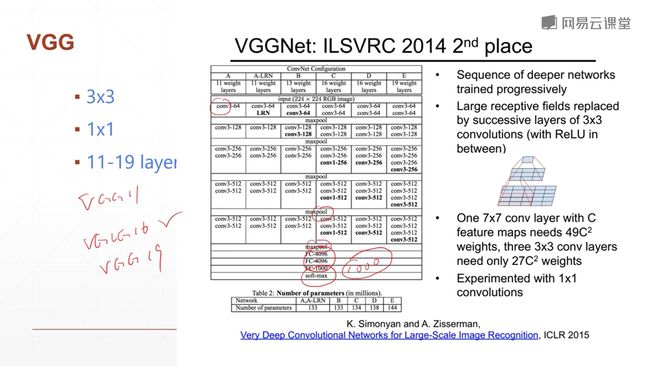
9.5.3 VGGNet
来自牛津大学的一个视觉研究组,他们一共发明了6种版本的网络结构。
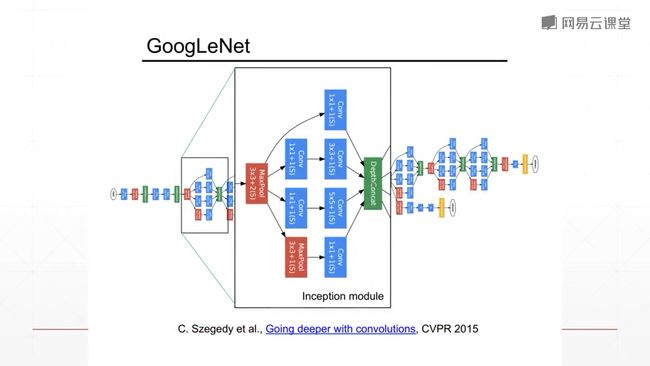
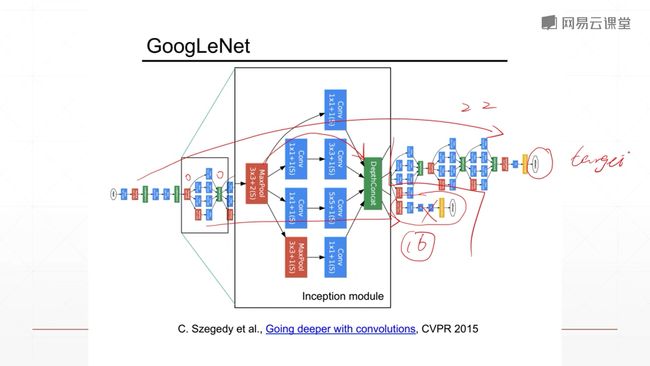
9.5.4 GoogleNet
Filter Concatenation 过滤器连接
Convolutions卷积
Previous Layer 上一层
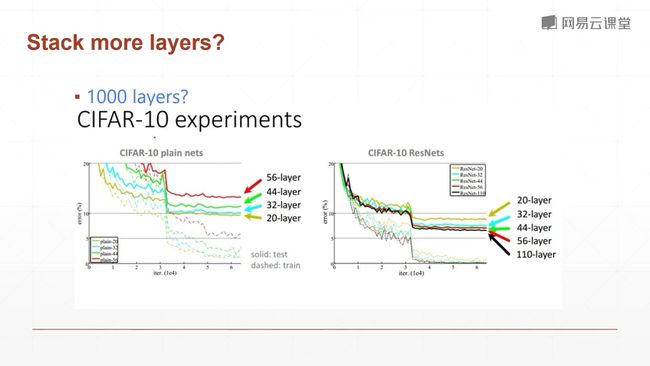
当层数更多的时候,22层左右以上,会导致training error会更高。
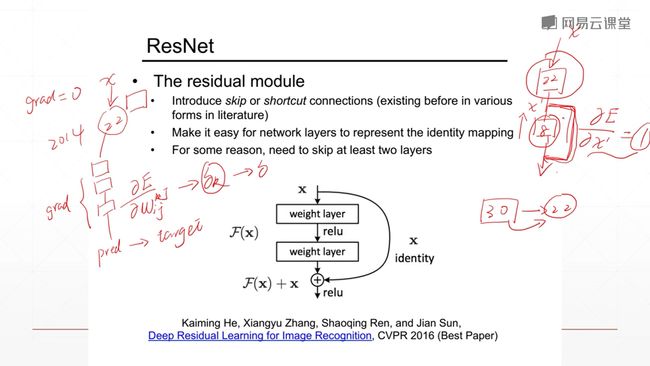
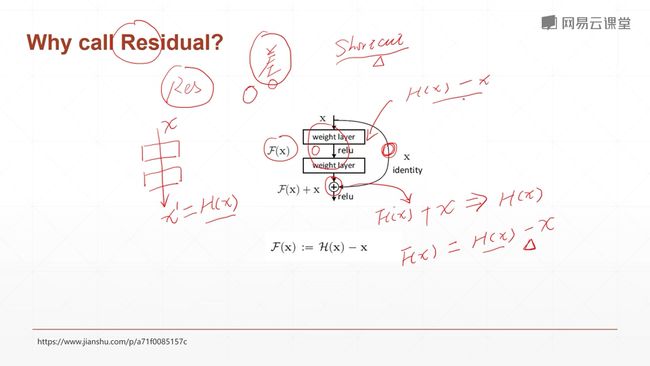
9.6 ResNet(何凯佲)
当前使用最广泛,意义影响最大的神经网络的变种。
华人研究学者,何凯佲在微软亚洲研究院研究出来的。
更深层次的网络,会出现梯度弥散(更新慢甚至不更新)和梯度爆炸(频繁更新,找不到最优解)的情况。
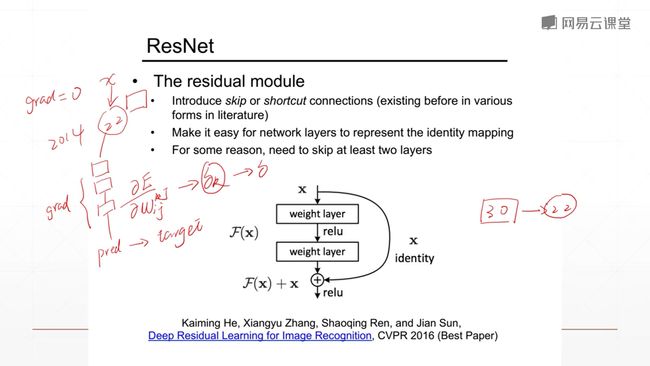
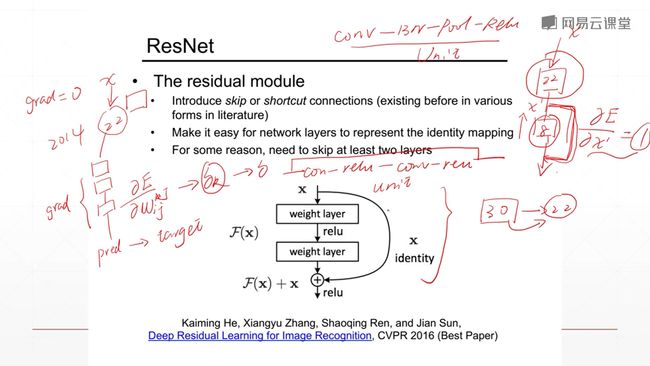
通过增加一个shortcut 捷径或者短路连接,使得你22层以上,更多层的网络连接的结果至少和22层的效果一样。因为你在这里加了一个x,你反向求导的时候的时候梯度的传播就不会进行衰减,因为求导的结果是1,任何学习率乘1结果还是那个数,不会出现梯度弥散的情况。
而这个shortcut具体实现起来呢,不是对后面的所有层搞一个shortcut,而是对每多少层就加一个shortcut。
空白意味着,如果你Resnet退化成一个直连,至少可以获得等同于一个vgg19的效果。Resnet对每个单元增加一个shortcut,所以说每个单元都可以退化成一个shortcut。退化的权利是交给这个网络去train的,就是这个网络它可以有一个选择权,它可以退化到一个更浅层次,如11层或者19层,来保证它的一个准确率。然后在你退化到这一层以后,你的准确率达到要求之后,也就是在网络训练好了之后,网络会想办法把退化掉的单元来训练上来,看能不能在已有的基础上再提升一点点。所以resnet就是这样一步一步train出来的。
当以后的优化技术变好了之后,那么resent可能就和vgg一样,变成一个中间产物了,但是目前来看的话,优化技术还达不到这个程度。因此我们认为来加了一个短接线,是的它train起来变得更加简单了。
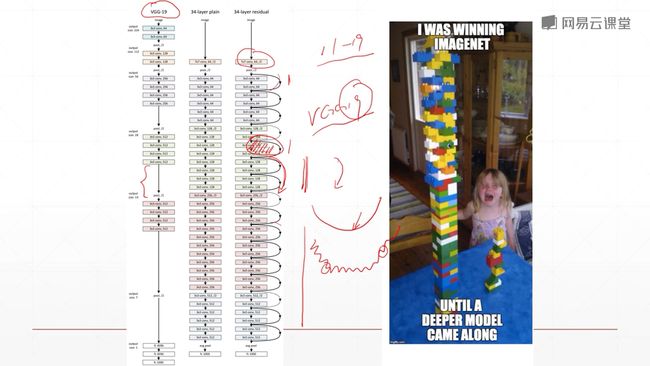
对于优化器来说,你加了shortcut,它优化起来更加的方便、快捷、有效。
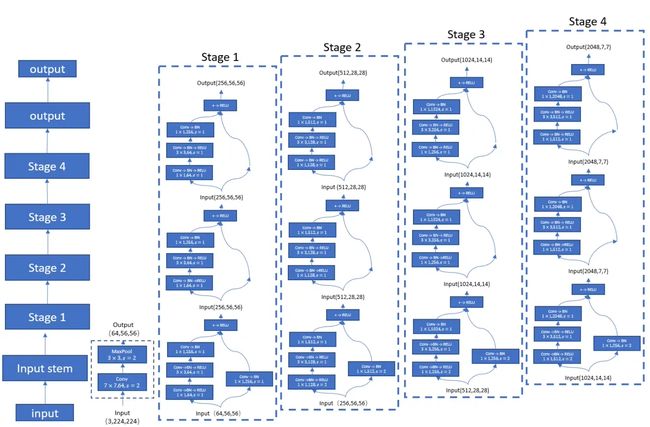
ResNet实现:
input和output不一致时的残差网络实现版本:
9.7 InceptionNet
是GoogelNet的下一个版本,加深的版本,略,有兴趣可以去了解一下。