AcWing 1064. 小国王（棋盘式状压dp 井字形）

本题是“井字形的约束摆放”，即：当前位置周围 8 个位置不能摆放棋子。

题意：

如题。

思路：

题目限制：当中间摆放了一个国王之后，其相邻的 8 个格子就不能摆放了。

如下图

当前行用什么方式摆，只和其上一行有关系，仔细想想就可以知道，其上上行无论是什么方式摆，都影响不到当前行

状态表示：f[i, j, s] 三维表示

集合：所有只摆在前 i 行，当前摆放了 j 个棋子，且最后一行的状态为 s 的方案集合
（s 是一个二进制的数，如果棋盘有 n 列，那么 s 即为一个 n 位的二进制数，0 表示空位，1 表示摆放了 1 个棋子）

属性：Count 方案数

状态计算：

f[i, j, s] 集合划分：当前最后一行状态已确定，我们集合划分的依据是倒数第 2 行的状态（最后一个不同点），无任何限制情况下，最多有 2 ^ n 种不同的情况

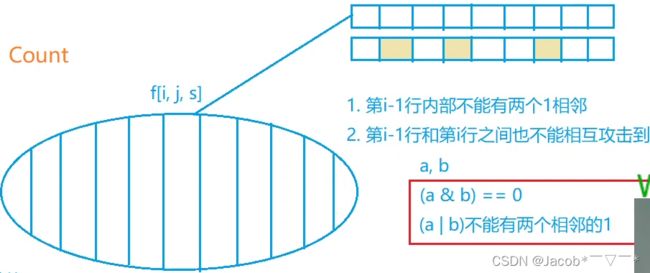
对于倒数第二行的状态，根据题意需要满足两个性质：首先两两国王不可相邻，其次受最后一行状态的制约（和最后一行不能相互攻击），比如下面这个倒数 1、2 行的情况就是一个合法情况

对于第一个性质，我们可以编写一个check函数进行判断是否满足它：

bool check(int st)
{
    for(int i=0; i>i&1) && (st>>(i+1)&1)) return false;
    }
    return true;
}

那么第 2 条性质如何用代码实现呢？设倒数第 1 行状态为 a，倒数第 2 行状态为 b。

那么要满足：

• (a & b) == 0
• (a | b) 不能有两个相邻 1，即：check( a | b ) = true

如果集合当中的某一类子集只有满足了两条性质时，直接加上这一类方案数量即可，对于这一类的方案数量，我们可以这样分析：

这一类集合的含义：已经摆完了前 i 排，并且第 i 排的状态是 a，第 i-1 排的状态是 b ，已经摆了 j 个国王的所有方案。

我们可以利用一个映射的思想，由于这类子集所有方案的最后一排状态都是 a，那么在求方案数的时候可以先将每个的方案的最后一行去掉，

即表示为 已经摆完前 i-1 排，并且第 i-1 排的状态是 b，已经摆了 j-Count(a)（Count(a) 表示 a 中 1 的个数） 个国王的所有方案：f[i-1, j-Count(a), b]。

从这里可以看出还需要计算一个二进制数的位数，可以用 c++ 的内置函数，也可以编码实现如下：

int count(int st)
{
    int cnt = 0;
    for(int i=0; i>i&1) ++cnt;
    }
    return cnt;
}

之后再统计其方案数，这时的方案数同样也是正确的，两者是一一映射的关系，

最后计算目标值 f[i, j, s] 时，只需要将 所有满足两个性质的子集 加在一起即可。

时间复杂度：

公式：状态数量 × 状态转移的计算量

行数（i：10）× 国王数（j：100）× 所有合法的状态数量（s：最坏情况下2 ^ 10）× 每个状态合法转移数量（sh：最多1000次转移）= 1e9

算出来是个很危险的时间复杂度，但是我们发现并不是所有的状态都合法，因为满足 “每一行不能有相邻的1” 这样的状态本来就很少，通过编程，我们发现，s、sh两者的乘积最大是 1365，因此实际上本题的时间复杂度很小，大约只有 1e6。

代码：

代码的一些细节：

• ①关于预处理

• 我们用一个 vector 数组 state 预处理 所有合法（两两国王不相邻）的状态，

• 用 head 二维变长数组 预处理 能够两两相互合法转移的状态，如 head[a] = b 表示状态 a 能由状态 b 合法转移而来

• cnt 数组 预处理 每一个二进制的压缩状态有多少个位为 1

• ②关于初始化状态

• 三维 dp 数组，第一维表示当前已摆好的行数，第二维表示放置国王数，第三维表示最后一行的状态

• 对于 dp 数组的初始化，我们根据实际出发即可，dp[0][0][0] 代表已经摆完前 0 行，且摆放国王数为 0 ，最后一行状态为 0 的方案数，* 显然这种情况是可以有 1 种合法方案的，初始化为 1 即可。

• ③关于目标状态的输出（答案）

• 我们可以观察到，如果当前层的一个棋子都不摆，即 state=(000000)，那么 所有合法的状态 都是 该状态的合法转移状态

• 也就是说：只要这层不摆东西，则上一层 只要合法，那一定可以转移到这一层的这个状态

• 因此我们可以把目标状态设为 f[n+1, k, 0]

• 该状态表示为：考虑前 n+1 层的棋盘，前 n+1 层放置了 k 个国王，且第 n+1 层什么也没放的方案

• 根据我们之前提到的 状态转移 可知，该状态会把所有到第 n 层的 合法状态 都转移到自己身上

• 这样最后我们就不需要额外枚举所有的目标状态了

#include

using namespace std;

#define int long long
const int N = 12, K = N * N, M = 1< state;
vector head[M];
int cnt[M];
int dp[N][K][M];

bool check(int st)
{
    for(int i=0; i>i&1) && (st>>(i+1)&1)) return false;
    }
    return true;
}

int count(int st)
{
    int cnt = 0;
    for(int i=0; i>i&1) ++cnt;
    }
    return cnt;
}

signed main()
{
    cin>>n>>k;
    for(int i=0; i<1<=c)
                    {
                        dp[i][j][a] += dp[i-1][j-c][b];
                    }
                }
            }
        }
    }
    cout<