八大基本排序与计数排序
文章目录
- 前言
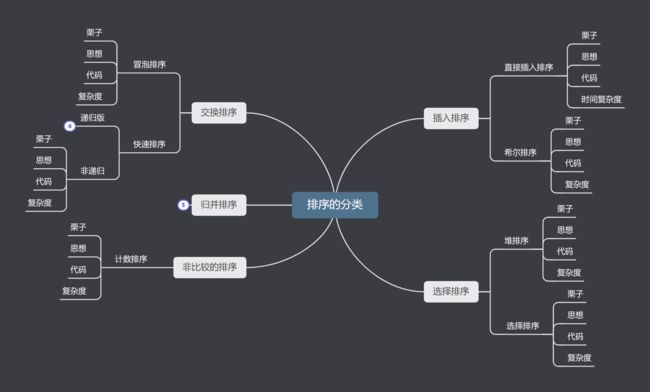
- 思维导图
- 排序的概念
- 插入排序
-
- 直接插入排序
-
- 栗子
- 思想
- 代码
- 复杂度
- 稳定性
- 希尔排序
-
- 栗子
- 思想
- 代码
- 代码分析
- 复杂度
- 稳定性
- 选择排序
-
- 选择法排序
-
- 栗子
- 思想
- 代码
- 复杂度
- 稳定性:
- 堆排序
-
- 思路
- 效果
- 代码
- 复杂度
- 交换排序
-
- 冒泡排序
-
- 栗子
- 思想
- 代码
- 复杂度
- 稳定性
- 快速排序递归版
-
- hoare版
-
- 栗子
- 思想
- 代码
- 时间复杂度
- 空间复杂度
- 挖坑法
-
- 栗子
- 思想
- 代码
- 时间复杂度
- 空间复杂度
- 前后指针法
-
- 栗子
- 思想
- 代码
- 时间复杂度
- 空间复杂度
- 快速排序非递归
-
-
- 思想
- 代码
- 复杂度:
- 快排的递归与非递归的比较
-
- 快排稳定性
- 归并排序
-
- 归并排序递归版
-
- 基本思想:合并2个有序数组
- 思想
- 代码
- 时间复杂度
- 归并排序的非递归
-
- 思想
- 代码
- 稳定性
- 非比较排序
-
- 计数排序
-
- 栗子
- 思想
- 代码
- 时间复杂度
- 稳定性
- 应用环境
- 各排序复杂度分析及稳定性汇总
前言
- 本文介绍八大排序:选择,冒泡,插入,希尔,堆排,快排,归并,计数,下面的数据都以
升序的形式排序- 动态图来源:https://visualgo.net/zh/sorting
- 自制思维导图自来源:幕布APP
- 博主收集的资料New Young,连载中。
- 博主收录的问题:New Young
- 转载请标明出处:New Young
思维导图
排序的概念
- 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
- 稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,那么称这种排序方式为稳定排序。
- 稳定性的应用场景:成绩排名,如果有相同成绩的2人,就以他们交试卷顺序来排名—-这是一种情景法,如有雷同,纯属巧合,
- 内部排序:数据元素全部放在内存中的排序,
- 外部排序:数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。当然,这仍然需要将外存的数据放到内存中。
- 下面介绍的排序都可以处理内存,因此都是内排序,但是归并排序,可以是外排序----排序文件。----在归并的应用环境会着重介绍怎么排序文件
插入排序
直接插入排序
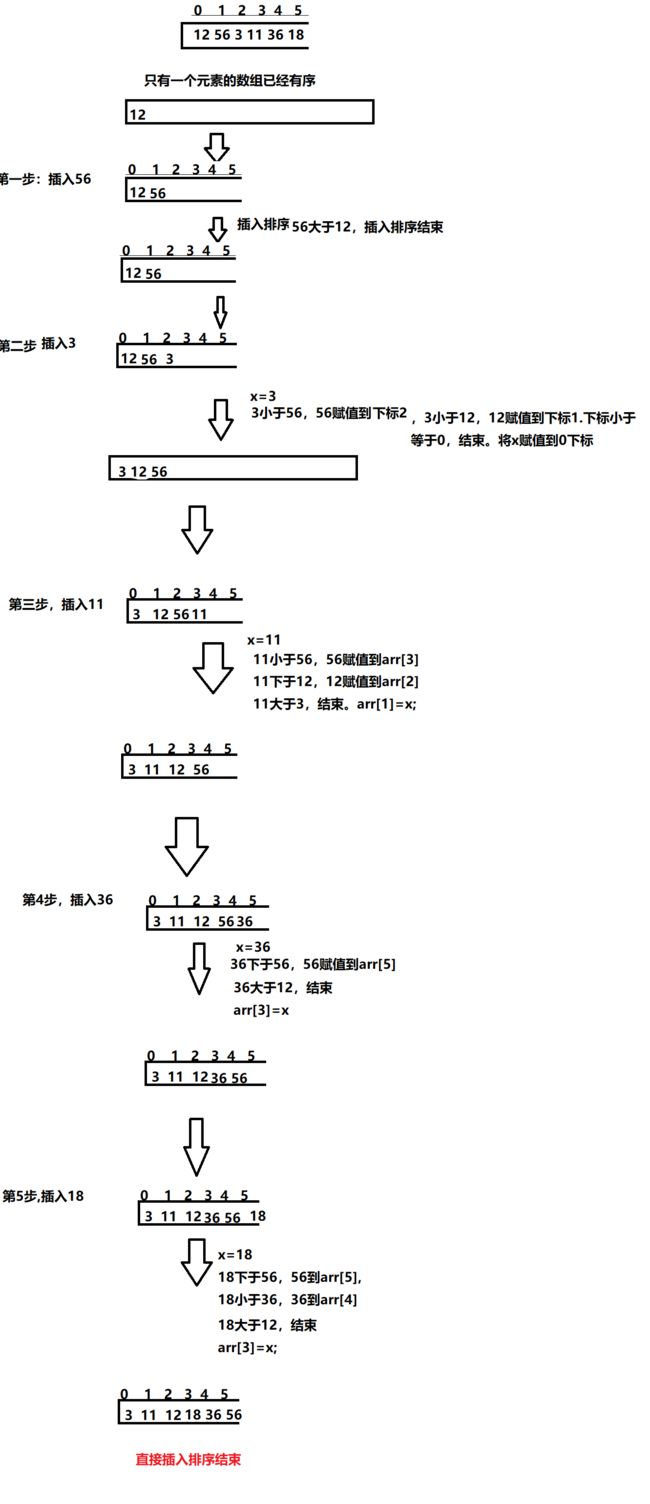
栗子
思想
以升序的形式讲述;
- 直接插入排序:在一个有序的数组中,如果你想插入一个数据,那就需要你从数组尾开始,去倒着比较数组中的元素,因为数组已经是有序的,如果小于数组中的元素就Swap,直到不在小于,找到自己在数组中的位置。
- 理解插入排序的关键是 ;数组已经有序且只有一个元素的数组就已经是有序的
- 如何做到只有一个元素呢?我们只需要从数组下标0开始,依次插入0之后的每个元素就行了,这样在插入新的元素前,它前面的元素已经通过
插入排序变为有序了。
代码
void InsertSort(int* a, int n)// 插入排序
{
assert(a);
for (int i = 0; i < n - 1; ++i)
{
int x = a[i + 1];
int end = i;
while (end >= 0)
{
if (a[end] > x)
{
a[end + 1] = a[end];
}
else
{
break;
}
end--;
}
a[end + 1] = x;
}
}
复杂度
空间复杂度:最好的情况:数组已经有序或者数组中部分无序。
已经有序,每次遍历一次,O(N)
部分无序,即使加上部分无序的遍历次数,也不会比N大多少,因此O(N)。
最坏:每次插入都遍历到头
Fn=1+2+…+N-1 =N*(N-1)/2=O(N^2)
空间复杂度:O(1)
稳定性
稳定,因为算法,只有遇到下于的,才向前Swap()。
希尔排序
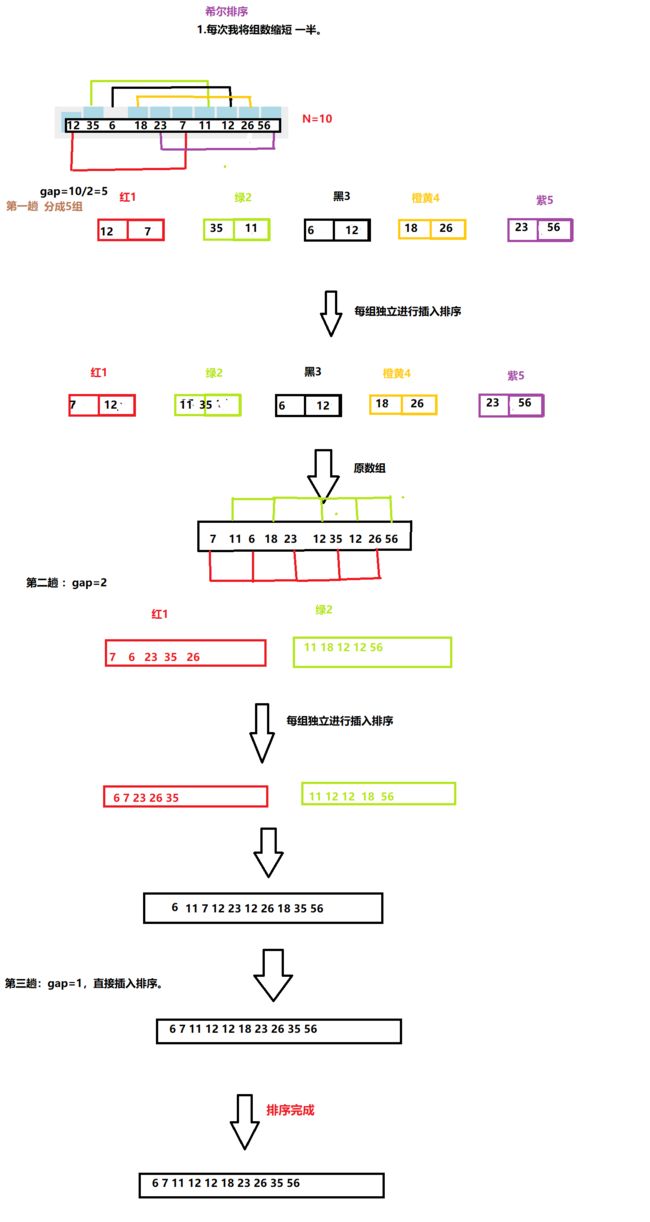
栗子
思想
以升序的形式讲述;
希尔排序:在插入排序最好的情况中 如果数组部分无序,可以达到O(N);
大致计算时间复杂度:Fn=(1+2+3+…+N/gap)*gap
gap越大,插入排序会更快。
gap越小,插排越慢。
因此希尔排序是基于插入排序,先将无序的数组分成gap
(一般第一次取N/2)组,对每组进行插入排序达到部分有序,这样逐渐减小gap,重复上述步骤,直到数组完全有序(gap==1时,进行直接插入排序)虽然看着不咋滴,但是在测试中,要比插入快很多。
代码
void ShellSort(int* a, int n)// 希尔排序
{
assert(a);
int gap = n;
while (gap>1)
{
gap /= 2;
for (int i = 0; i < n - gap; ++i)
{
int end = i;
int x = a[end + gap];
while (end >= 0)
{
if (a[end] > x)
{
a[end + gap] = a[end];
}
else
{
break;
}
end -= gap;
}
a[end + gap] = x;
}
}
}
代码分析
复杂度
时间度杂度:O(N^1.3),博主实力有限,不会。
空间度杂度:O(1)
稳定性
不稳定。因为可能会被分到不同组。
选择排序
选择法排序
栗子
思想
以升序的形式讲述;
选择法:从数组中选择一个元素,记录它的下标记录到Small,之后将Small
依次与数组中的其它元素进行比较,如果有小于它的元素,就记录新的下标,这样遍历到最后,我们会发现留到Small中的就是最小元素的下标。这就像斗地主一样,我们排序手中的牌,从第一张牌开始,将牌中最小的与它Swap().为什么使用下标的方式而不是像冒泡那样用值。
因为 如果用值,虽然最后到我们手上的是最小的值,但是它在数组中的下标是不可知,也不可以用Swap().
- 一次选择只能找到一个最小的,因此要排序所有,需要进行N趟,及时只有一个也要选择排序
- 这里我一次性找到最大和最小的下标。这样可以将趟数缩减为N/2.
代码
void SelectSort(int* a, int n)// 选择排序
{
assert(a);
for (int i = 0; i < n / 2; ++i)
{
int begin = i;
int end = n - 1-i;
int max = i;
int min = i;
for (int j = begin; j <= end; ++j)
{
if (a[j] > a[max])
{
max = j;
}
if (a[j] < a[min])
{
min = j;
}
}
//如果下标改变了,就代表选择出了最大,最小数据对应得下标。
if (max != i)
{
Swap(&a[max], &a[i]);
}
if (min != i)
{
Swap(&a[min], &a[i]);
}
}
}
复杂度
选择排序很特殊,无论何时,它都要遍历一遍数组O(N)
如果一次就选择了一个,那么Fn=N*N=O(N^2)
如果选择2个,Fn=N/2 *N =O(N^2)
因此发现,选择无论怎么处理,它的时间复杂度始终是O(N^2)
空间复杂度:O(1)
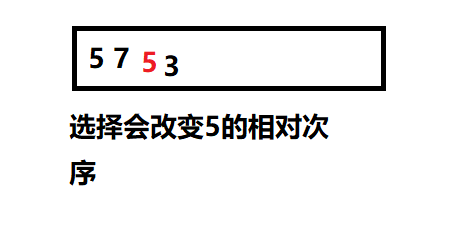
稳定性:
不稳定。
堆排序
思路
我们再删除堆操作中,先将头尾交换,之后对头向下调整。再结合堆的根结点是
最值.如果我们每次都将堆的根结点与尾交换,然后将尾前面就行向下调整,这样就可以完成排序。如果想
降序,因为最大值在最后,所以要求第一个根结点是最大值,这就要求我们建大堆,让根结点成为最大值。反之,升序,建小堆。
效果
代码
// 降序,建小堆,跟结点必然是最小结点,
//所以首尾交换后,跟的左右子树仍是关系未破坏的堆,
//所以可以通过向下调整的方式,再次选出最小的结点,
//重复改过程。
void HeapSort(HPDataType* a, int n)
{
assert(a);
//建堆
//
//
//
//方式一:向上调整算法
//for (int i = 1; i < n; ++i)
//{
// Adjustup(a, i);
//}
//HeapPrint(a, n);
//方式二,非递归向下调整算法。
//方式二:在数组上操作
//思路:只有一个结点也是堆,通过插入,向下调整,建堆。
//for (int parent = (n - 1 - 1) / 2; parent >= 0; --parent)
//{
// Adjustdown(a, n, parent);
//}
//printf("向下调整结果\n");
//HeapPrint(a, n);
方式三,递归向下调整算法建堆
//
//递归法建堆
printf("递归向下调整结果\n");
RecDown(a, n, 0);
for (int i = 0; i < n-1; ++i)
{
Swap(&a[0], &a[n -1- i ]);
Adjustdown(a, n-1-i, 0);
}
}
复杂度
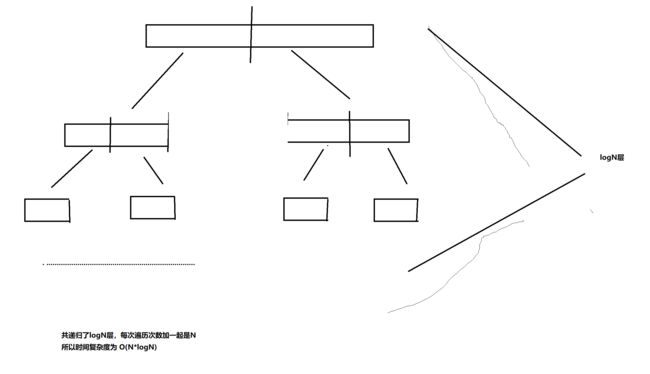
时间:每次讲堆顶元素置换到尾后,要向下调整----但是向下调整次数是与N有关的–logN,由于不断的重新建堆,要排序的堆大小逐渐减小。
因此可以 Fn=log2+log3+…+logN。
数学可以证明:Fn与N*logN是近似相等的------博主数学不行,无法证明。
因此堆排的时间复杂度为:O(N*logN)
空间复杂度:因为是在原数组上建堆的,所以空间复杂度为O(1)
交换排序
冒泡排序
栗子
思想
以升序的形式讲述
冒泡排序是:在遍历一趟数组过程中,持续的比较数组中相邻的2个元素,如果
arr[n]>arr[n+1],那么就交换swap(arr[n],arr[n+1]).这样的话,大的数据就会存到arr[n+1];此时在比较arr[n+1]与arr[n+2]…….这样反复操作,我们会发现最大的数被排序到最后了。这就像水杯中的泡泡,最大的泡泡总是冒到最上面,而小的在最下面。冒泡的每趟将最大的排的后面,之后就不需要在处理这个数据,因此冒泡的区间会不断减小。
对于N个元素的数组,只需要减小N-1趟(当只有一个元素时,是不需要进行冒泡的)。
如果数组在第一趟未发生 交换,说明数组已经是有序的,不需要冒泡了。因此这里用flag来标记
代码
void Swap(int* a, int* b)
{
assert(a && b);
int tmp = *a;
*a = *b;
*b = tmp;
}
//冒泡的每趟将最大的排的后面,之后就不需要在处理这个数据,因此冒泡的区间会不断减小。
//对于N个元素的数组,只需要减小N-1趟(当只有一个元素时,是不需要进行冒泡的)。
//如果数组在第一趟未发生 交换,说明数组已经是有序的,不需要冒泡了。因此这里用flag来标记
void BubbleSort(int* a, int n)// 冒泡排序
{
assert(a);
int flag = 0;
//外层控制趟数,内存遍历与交换。
for (int i = 0; i < n - 1; ++i)
{
for (int j = 0; j < n -1- i; ++j)
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
flag = 1;
}
}
if (0==flag)
{
break;
}
}
}
复杂度
最好情况:数组恰好是有序的,只需要遍历一遍数组就可以结束冒泡排序,因此是O(N)
最坏的情况:第一趟:遍历N次
第二次: 遍历N-1次
第N-1趟:遍历2次。
Fn=N+N-1+…+1=(1+N)*(N-1)/2
因为时间复杂度看的是大致,所以O(N^2);
空间复杂度:O(1)
稳定性
稳定,因为相同的值,是不需要交换的,并不会改变他们的相对次序。
快速排序递归版
快速排序的基本思想:通过选定数组中的一个元素key,一般选择数组的 最左边或者最右边元素(中间会有些麻烦),通过交换,最终让key左边都是下于它的,右边是大于它的,然后将区间分成2部分,对这2部分重复该过程。我们很轻易发现,快排是一个递归概念。
在区间操作中的算法(单趟排序),有3个版本:
hoare版
这是快排创始人hoare发明的方法
- 挖坑法
这是绝大部分大学教材所统一采用的方法
- 前后双指针法
hoare版
栗子
思想
以升序的形式讲述;
- hoare版:选定数组最左边下标为
key,从最右边开始选择出小于key的数据下标为right,从左边key+1开始,找出大于key的数据下标为left。然后Swap(arr[left],arr[right]).重复该步直到left和right相遇,Swap(arr[key],arr[left])
从左开始,从右找最小。—因为小的必然要跑到左边,本来就小的留在了左边。
如果选定最右边下标为key,则从最左边开始,先找最大的,然后从右边找小的。
从右开始,从左找最大。—因为大的必然要跑到右边,本来就大的留在了右边。
相遇点一定小于key(有点抽象,建议自己画图理解)
交换后,right下标对应是大于key的,left对应的是小于right,正是因为这样,才能让最后key和left交换时,保证left对应的值不可能大于key。如果真的存在大于,那么有2种情况:恰好是从右找大的,这里仍然要交换;如果是从左找小的,那么right会越过这个。但是这2种情况,都不会让相遇点大于key。因此相遇点一定小于key
为什么一定是从左始,从右找小
假设从左开始:本来就小的会留在左边,因此从右边找小。
为什么一定是找小的先开始,找大的后开始:
因为交换后,right的值会大于key,left会下于key。如果再从左边先找大的可能会导致,找到的是right位置的值。
如果数组本来就是有序的,快排会发生什么呢?—正常快排方法无法解决有序数组问题,因此三数取中。
递归过深,栈溢出。
如果是有序(升序)的数组,找小直接到达最左边,之后将区间分为2份时,左区间就一个数据,右区间有N-1个,此后右区间递归继续以这样的2分,这样导致,程序为每个数据都进行了函数栈帧,栈很小且有限,溢出是必然的。
解决方法:打乱有序,每次单趟都三数取中(头,尾,中间比较,找中间值与left交换)。
代码
int GetMidIndex( int* a, int left, int right)//三数取中
{
assert(a);
int mid = (left + right) / 2;
if (a[left] >= a[mid])
{
if (a[mid] >= a[right])
{
return mid;
}else//a[mid]
{
if (a[right] > a[left])
{
return left;
}
else
{
return right;
}
}
}
else//a[left]
{
if (a[mid] < a[right])
{
return mid;
}
else//a[mid]>=a[right],mid是最大的
{
if (a[right] > a[left])
{
return right;
}
else
{
return left;
}
}
}
}
int PartSort1(int* a, int left, int right)// 快速排序hoare版本
{
assert(a);
//三数取中,是为了解决有序,栈溢出的问题。
//通过取中,打乱有序。
int key = GetMidIndex(a,left,right);
Swap(&a[key], &a[left]);
int keyi = left;
while (left<right)
{
while (right>left && a[right] >=a[keyi])//从右开始,找第一个小于a[key]
{
--right;
}
while (left<right && a[left] <= a[keyi])//从左开始,找第一个大于[key]
{
++left;
}
Swap(&a[left], &a[right]);
}+
Swap(&a[keyi], &a[right]);
return left;
}
void QuickSort(int* a, int left, int right)
{
assert(a);
if (left >= right)
{
return;
}
if (right - left<10)//小区间优化,这可以减少递归的深度。
{
InsertSort(a+left, right - left + 1);
}
else
{
int key = PartSort1(a, left, right);*/
//int key = PartSort2(a, left, right);
//int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
}
时间复杂度
空间复杂度
递归的深度在logn到N
所以空间复杂度为:O(logN 到N)
挖坑法
栗子
思想
以升序的形式讲述;
- 看栗子
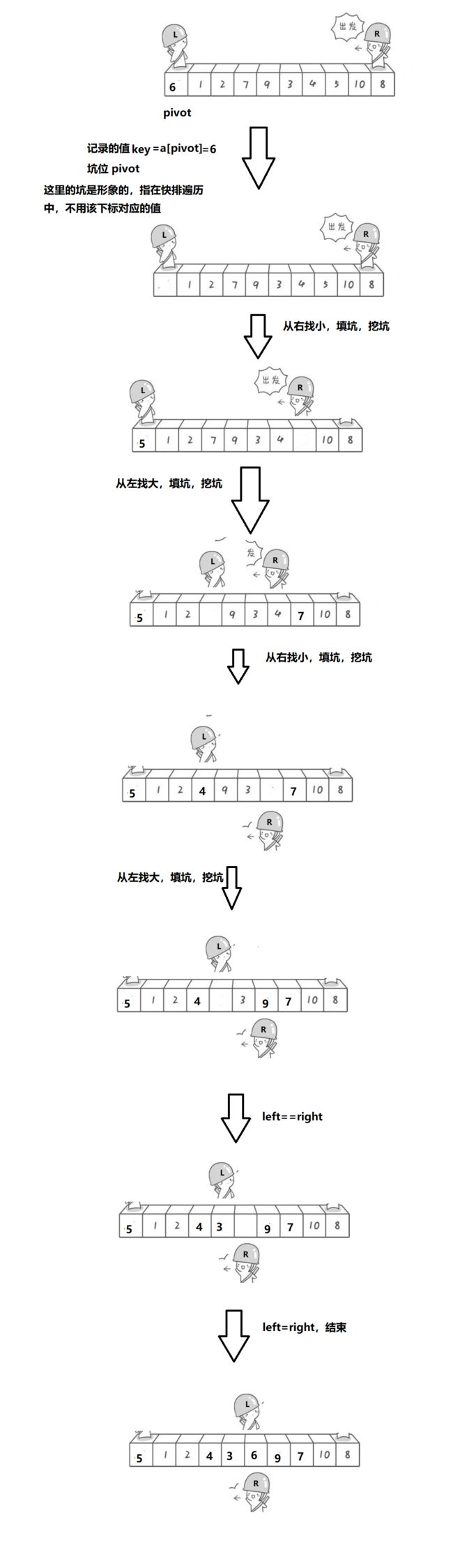
- 挖坑法:记录区间的最左边的值key和他的下标—坑位pivot,从右边找小,找到了就与坑位pivot交换数据,同时将right赋值给pivot—
填坑,新成新的坑位—换坑。之后从左找大,找到就填坑,换坑.重复上述过程,直到left和right相遇,然后将记录的值key填到坑中。然后分成2个区间,继续递归。
代码
int PartSort2(int* a, int left, int right)// 快速排序挖坑法
{
assert(a);
int tmp = GetMidIndex(a, left, right);
Swap(&a[tmp], &a[left]);
int pivot = left;//坑
int key = a[pivot];
while (left < right)
{
while (right > left && a[right] >= key)//从右开始,找第一个小于a[key]
{
--right;
}
//填坑
a[pivot] = a[right];
//换坑
pivot = right;
while (left < right && a[left] <= key)//从左开始,找第一个大于[key]
{
++left;
}
//填坑
a[pivot] = a[left];
//换坑
pivot = left;
}
a[pivot] = key;
return pivot;
}
void QuickSort(int* a, int left, int right)
{
assert(a);
if (left >= right)
{
return;
}
if (right - left<10)
{
InsertSort(a+left, right - left + 1);
}
else
{
/*int key = PartSort1(a, left, right);*/
int key = PartSort2(a, left, right);
//int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
}
时间复杂度
和hoare一样 O(N*logN)
空间复杂度
递归的深度在logn到N
所以空间复杂度为:O(logN 到N)
前后指针法
栗子
思想
以升序的形式讲述;
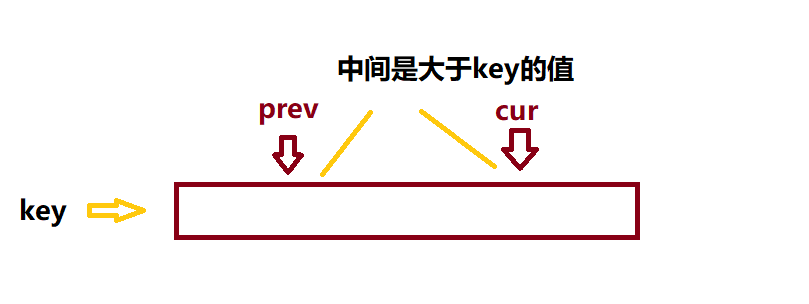
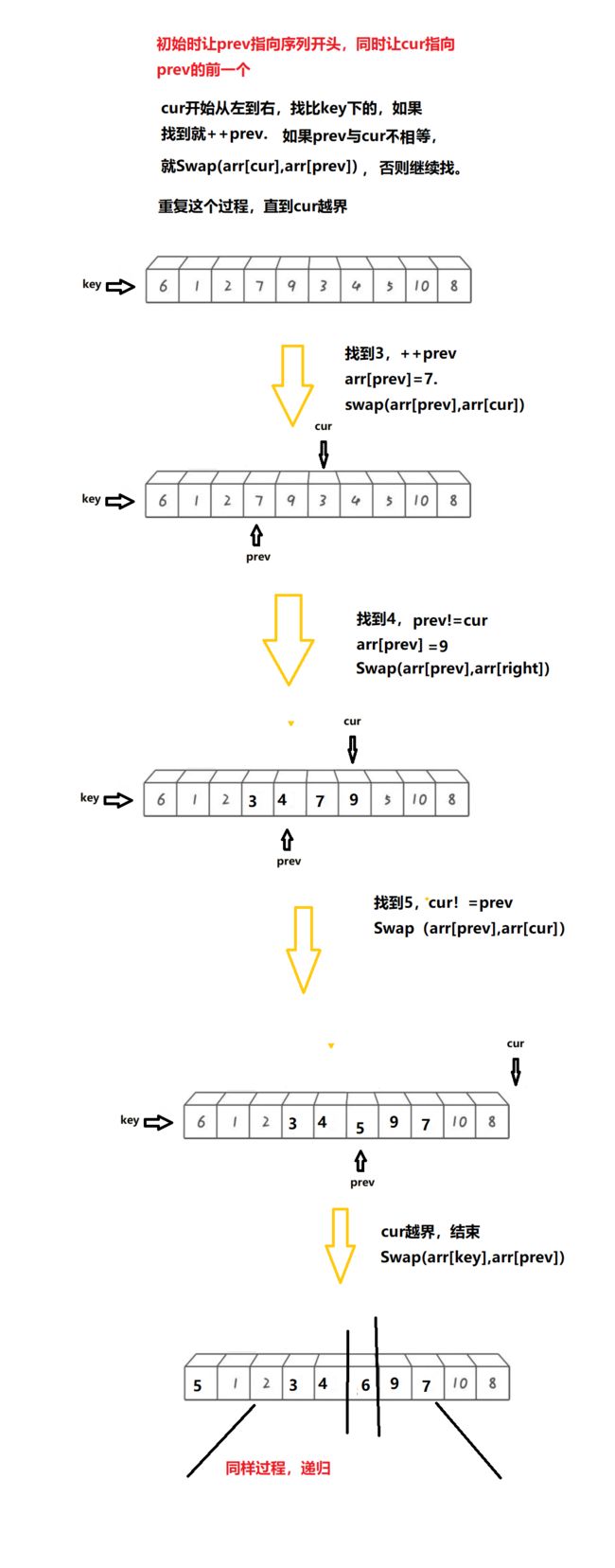
前后指针法:仍是着眼于快排的基本思想:让小的到左边,大的到右边。
记录序列的头为key,让一个找小的快指针(cur)从
key+1开始先走,这样一些大的值会被略过,也正因为略过的原因,++prev就可以直接到一个大值。当然这有可能会出现,++prev后恰好与cure重合的情况,因此为了避免这种情况。我们在交换元素前,还要保证 prev!=cur.cur始终走在prev前面,又因为prev!=cur的限制,因此最终只能是cur越界。
代码
int PartSort3(int* a, int left, int right)
{
assert(a);
int prev = left;//慢指针
int cur = prev + 1;//快指针
int keyi = left;
//双指针法:cur的查找可以一次越过很多数值,但是prev只能越过一次---可以多次cur++,但是++prev只有一次
while (cur <= right)
{
if (a[cur] < a[keyi] && (++prev) != cur)
//++prev!=cur是为了当 ++prev与cur位置重合,避免没必要的交换
{
Swap(&a[cur], &a[prev]);
}
cur++;
}
if (prev <= right)
{
Swap(&a[keyi], &a[prev]);
}
return prev;
}
void QuickSort(int* a, int left, int right)
{
assert(a);
if (left >= right)
{
return;
}
if (right - left<10)//小区间优化,这可以减少递归的深度。
{
InsertSort(a+left, right - left + 1);
}
else
{
//int key = PartSort1(a, left, right);*/
//int key = PartSort2(a, left, right);
int key = PartSort3(a, left, right);
QuickSort(a, left, key - 1);
QuickSort(a, key + 1, right);
}
}
时间复杂度
O(logN*N)
空间复杂度
递归的深度在logn到N
所以空间复杂度为:O(logN 到N)
快速排序非递归
思想
函数栈帧发生在计算机的栈区,特点是:先进后出,先用低地址后用高地址
这和数据结构中的顺序表—栈几乎完全一样。因此既然递归发生在栈区—这个和数据结构中的栈类似的,为什么不可以用数据结构的栈来模拟炸区呢?
发现:快排的三种单趟排序用的是
数组下标,而且递归时也是用的下标,因此我们将数组下标的存到栈中就可以模拟了。
代码
void QuickSortNonR(int* a, int left, int right)
{
assert(a);
stack st;
StackInit(&st);
StackPush(&st, left);//入栈
StackPush(&st, right);//出栈
while (!StackEmpty(&st))
{
int end = StackTop(&st);//区间的右边界
StackPop(&st);
int begin = StackTop(&st);//区间的左边界
StackPop(&st);
int keyi = PartSort3(a, begin, end);//单趟,返回相遇点下标
//将二分区间的下标放到栈中
//递归先将右边递归玩,还是左边都一样,
//但是为了与递归快排保持一致,先存右区间,后存左,这样就可以先取左区间的下标,
//
//[begin keyi-1 ] keyi [keyi+1,end]
if (keyi + 1 < end)
{
StackPush(&st, keyi+1);
StackPush(&st, end);
}
if (keyi - 1 > begin)
{
StackPush(&st, begin);
StackPush(&st, keyi -1);
}
}
}
复杂度:
时间复杂度:O(N*logN)
空间复杂度:O(logN到N),一般取O(logN)
快排的递归与非递归的比较
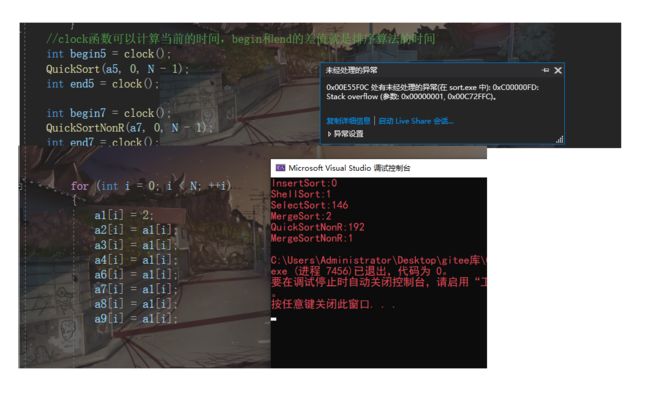
- 递归快排,一但遇到数组元素相同的,因为栈区很小,基本都会导致栈溢出(Stack Overflow),即使用了三数取中。而非递归的快排,利用的是数据结构中的栈—动态开辟利用堆区,堆区要比栈大区很,可以进行排序,但仍不是太好,因此一般对于这种全部相同的数组,用非递归快排,或者其他排序方式。
- 但快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
快排稳定性
不稳定。
归并排序
归并排序递归版
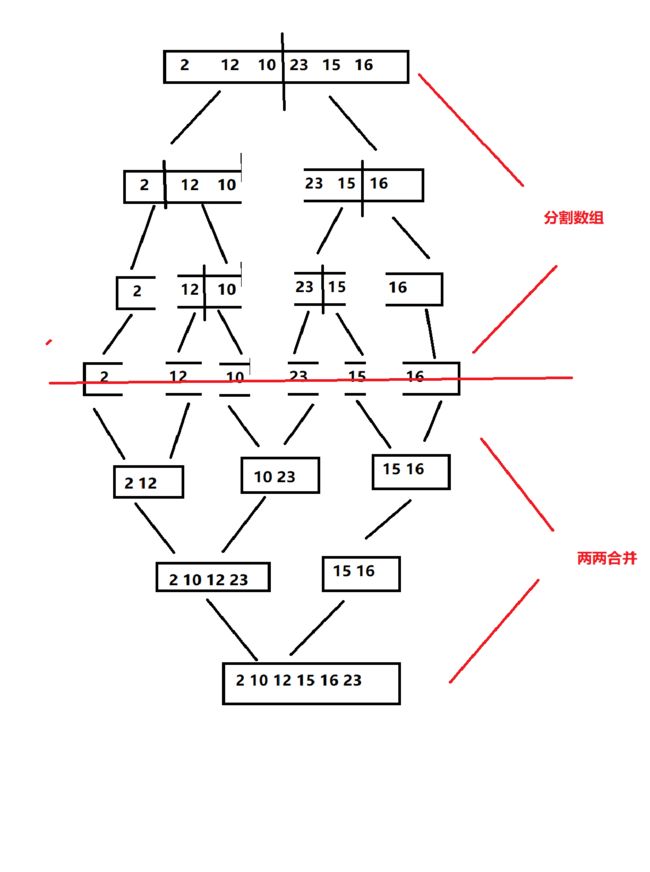
基本思想:合并2个有序数组
思想
关键:只有一个元素的数组是有序的。
因此归并排序是:先将数组递归成区间为1的数组,然后通过数组合并的思想来递推数组。
写出代码的关键是:控制下标,不然很容易出问题
代码
void _MergeSort(int* a, int* tmp, int left, int right)
{
assert(a);
if (left >= right)
{
return;
}
int mid = left+(right-left)/2;//防止溢出问题。
_MergeSort(a, tmp, left, mid);
_MergeSort(a, tmp, mid+1,right);
int begin1 = left;
int begin2 = mid + 1;
int i = begin1;
while (begin1<=mid && begin2<=right)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1<=mid)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= right)
{
tmp[i++] = a[begin2++];
}
//一定要将tmp再赋值给原数组,如果不赋值,再回归上一层时,进行数组合并时,数组仍是无序的。
for (int i = left; i <=right; ++i)
{
a[i] = tmp[i];
}
}
void MergeSort(int* a, int n)
{
assert(a);
int* tmp = (int*)malloc(sizeof(int) * n);
assert(tmp);
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
tmp = NULL;
}
时间复杂度
递归了logN层,每层都要遍历N次
因此时间复杂度为O(N*logN).
归并排序的非递归
思想
- 同快排的非递归一样利用栈。
- 类似直接插入排序,因为只有一个元素的数组是有序的
- 我们可以直接让数组元素两两合并后,再增加数组的大小,重复该过程。
- 只是在算法时,边界的控制相对来说比较麻烦,要多留意。
代码
void MergeSortNonR(int* a, int n)// 归并排序非递归实现
{
assert(a);
int * tmp = (int*) malloc( n*sizeof(int));
assert(tmp);
int gap = 1;//启始合并元素只有1的
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int index = i;
int begin1 = i;
int begin2 = i + gap;
int end1 = begin2 - 1;
int end2 = i + 2 * gap - 1;
//三种越界情形,begin1是不可能越界的,因为i的限制。
//同时判断也要依次判断,不然容易错误
if (end1 >= n)
{
end1 = n - 1;
}
if (begin2 >= n)//通过重新赋值,让b2>end2,不让进入循环即可。
{
begin2 = n + 1;
end2 = n;
}
if (end2 >= n)
{
end2 = n - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
}
//将tmp赋值到数组中。
for (int j = 0; j < n; ++j)
{
a[j] = tmp[j];
}
gap *= 2;
}
free(tmp);
tmp = NULL;
}
稳定性
稳定
非比较排序
计数排序
栗子
思想
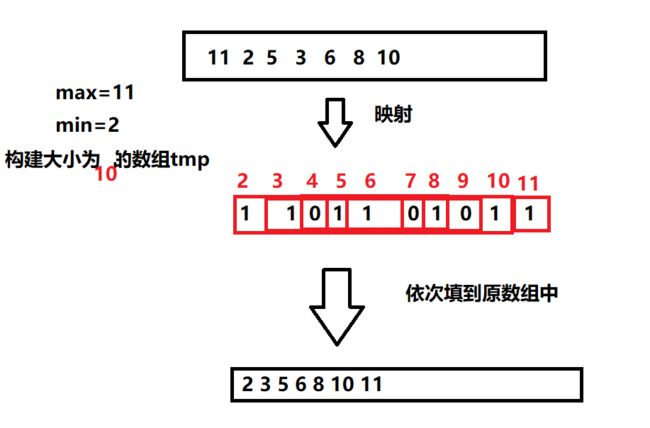
计数排序又称为鸽巢原理,是对哈希直接定地址的变形应用。
基本思想:遍历一遍数组arr,找出数组中的最大max,最小值min。动态开辟max-min+1大小的数组tmp。再次遍历数组,将数组中出现值,映射到tmp中,只是要注意min可能不是0,因此在数组下标从0+min开始。之后遍历tmp,从tmp的0+min开始,下标中的值是多少,就将下标复写到arr中。
可以看出计排是无法保证稳定性的。
计排对于浮点型数据是不行的,但是对于正数和负数都可以。
对负数排序的解决要自己画图理解,有点抽象。
代码
void CountSor(int* a, int n)// 计数排序
{
assert(a);
int max = Max(a, n);
int min = Min(a, n);
int N = max - min + 1;//得到要开辟数组的大小。
int* tmp = (int*)malloc(N*sizeof(int));
assert(tmp);
memset(tmp, 0, N*sizeof(int));
//tmp内存初始化为0;
//memest是在一字节大小的内存放入0,因此4字节大小的内存全是0,因此可以初始化为0.
//但是memset只能对一个字节放数据,因此如果连续的字节,所表达的数据就不对了
for (int i = 0; i < n; ++i)
{
tmp[(size_t)a[i] -(size_t)min]++;
//这种处理的方式是:即可以处理正数,也可以负数。
//如果是0+min的只能处理正数,。
}
int index = 0;
for (int i = 0; i < N; ++i)
{
while (tmp[i] !=0)
{
a[index++] = i+min;
tmp[i]--;
}
}
free(tmp);
tmp = NULL;
}
时间复杂度
计排基本都是在遍历,而这种遍历是无法达到O(N^2)的,当N很大是,N的倍数和N是没有区别的。当然也要考虑动态开辟数组的范围。
因此时间复杂度O(Max(N,范围)).
空间复杂度:O(范围)
稳定性
不稳定。相同值被映射到tmp数组后就没意义了。
应用环境
计数排序在数据范围集中时,效率很高,但是适用范围及场景有限
且不用于浮点型数据。
各排序复杂度分析及稳定性汇总
| 排序方法 | 时间复杂度最坏情况 | 空间复杂度 | 稳定性 |
|---|---|---|---|
| 直接插入排序 | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(N^1.3) | O(1) | 不稳定 |
| 选择法排序 | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N*logN) | O(1) | 不稳定 |
| 冒泡排序 | O(N^2) | O(1) | 稳定 |
| 快排 | O(N*logN) | O(1) | 不稳定 |
| 归并排序 | O(N*logN) | O(N) | 稳定 |
| 计数排序 | O(N) | 不稳定 |