灰色预测GM(1,N)代码

注：GM(1,1)代码

累加序列，生成新序列

import numpy as np
import math as mt
import matplotlib.pyplot as plt
# 1.这里将 a 作为特征序列 x0,x1,x2,x3作为相关因素序列
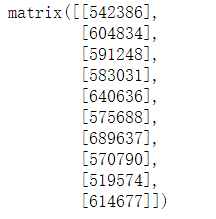
a = [560823,542386,604834,591248,583031,640636,575688,689637,570790,519574,614677];
x0 = [104,101.8,105.8,111.5,115.97,120.03,113.3,116.4,105.1,83.4,73.3]
x1 = [135.6,140.2,140.1,146.9,144,143,133.3,135.7,125.8,98.5,99.8]
x2 = [131.6,135.5,142.6,143.2,142.2,138.4,138.4,135,122.5,87.2,96.5]
x3 = [54.2,54.9,54.8,56.3,54.5,54.6,54.9,54.8,49.3,41.5,48.9]
 
# 2.累加序列，生成新序列
def AGO(m):
    m_ago = [m[0]]
    add = m[0] + m[1]
    m_ago.append(add)
    i = 2
    while i < len(m):
        # print("a[",i,"]",a[i])
        add = add+m[i]
        # print("->",add)
        m_ago.append(add)
        i += 1
    return m_ago
 
a_ago = AGO(a)
x0_ago = AGO(x0)
 
x1_ago = AGO(x1)
x2_ago = AGO(x2)
x3_ago = AGO(x3)```

```python
xi = np.array([x0_ago,x1_ago,x2_ago,x3_ago])
print("xi",xi)

紧邻均值生成序列

# 3.紧邻均值生成序列
def JingLing(m):
    Z = []
    j = 1
    while j < len(m):
        num = (m[j]+m[j-1])/2
        Z.append(num)
        j = j+1
    return Z
Z = JingLing(a_ago)
print(Z)#1行10列

求相关参数

# 4.求相关参数
#4.1 求Y
Y = []
x_i = 0
while x_i < len(a)-1 :
    x_i += 1
    Y.append(a[x_i])
#Y list
#化为矩阵，进行矩阵运算
Y = np.mat(Y).T
Y.reshape(-1,1)

#4.2 求B
B = []
b = 0
while b < len(Z) :
    B.append(-Z[b])
    b += 1
B = np.mat(B)#数组转矩阵
B.reshape(-1,1)#1*10
B = B.T
print("B.shape:",B.shape)

X = xi[:,1:].T#除第一列外（因为最终B是从x2(1) 2 开始）的所有行所有列，并转置
print("X.shape:",X.shape)#10*4

B = np.hstack((B,X))#合并，B和X元组的元素数组按水平方向进行叠加
print("B-final:",B.shape)

由上一步求出参数

#5 由第四步求出参数
#用最小二乘参数估计，求出参数theat（含发展系数al->theat[0,:],驱动系数b->theat[1:ehd-1,:])
theat = np.linalg.inv(B.T.dot(B)).dot(B.T).dot(Y)
print(theat)

#5.1 发展系数
al = theat[:1,:]
#print(type(al))
al = float(al)
#print(type(al))
al

#5.2 驱动系数b
#import pandas as pd
b = theat[1:,:].T#除第一行外（因为最终B是从Z(1) 2 开始）的所有行所有列，并转置，
#pd.DataFrame(b).to_excel("new11.xlsx")
print("b.shape:",b.shape)#1*4 矩阵
b = list(np.array(b).flatten())#转数组
b

生成预测模型

# 6.生成预测模型
#6.1 计算驱动值 bixi(1)k
U = []
k = 0
i = 0
for k in range(11):
    sum1 = 0
    for i in range(4):
        sum1 += b[i] * xi[i][k]
        #print("第",i,"行","第",k,'列',xi[i][k])
        i += 1
    #print(sum1)
    U.append(sum1)
    k += 1
print("U:",U)

#6.2 求解微分方程，计算完整公式的值
F = []
F.append(a[0])
f = 1

while f < len(a):
    F.append((a[0]-U[f-1]/al)/mt.exp(al*f)+U[f-1]/al)
    f += 1

print("F=",F)

#6.3 累减还原，得原始数列的灰色预测值
G = []
G.append(a[0])
g = 1
while g<len(a):
    G.append(F[g]-F[g-1])
    g +=1
print("G:",G)

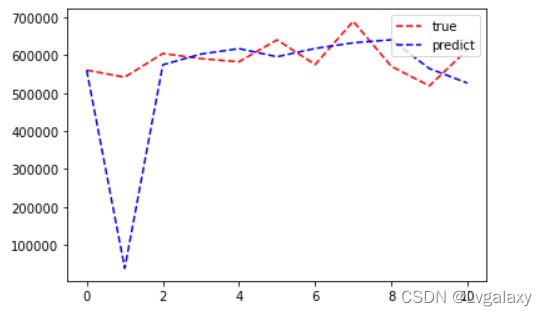
可视化

r = range(11)
t = list(r)

plt.plot(t,a,color='r',linestyle="--",label='true')
plt.plot(t,G,color='b',linestyle="--",label="predict")
plt.legend(loc='upper right')
plt.show()

残差检验

#7.1绝对误差序列
'''import numpy as np
A=np.array(a)
G00=np.array(G)
abc=abs(A-G00)
abc简化'''
def abERR(m,n):
    err =[]
    i = 0
    while i < len(m):
        num = abs(m[i]-n[i])
        err.append(num)
        i += 1  
        
    return err
abErr=abERR(a,G)
#7.2相对误差序列
def oppERR(m,n):
    err =[]
    i = 0
    while i < len(m):
        num = m[i]/n[i]
        num1=str(num*100) + '%'
        err.append(num1)
        i += 1  
        
    return err
oppErr=oppERR(abErr,a)

#7.1 计算原始序列标准差S1
def MEAN1(m):
    add =0
    i = 0
    while i < len(m):
        # print("a[",i,"]",a[i])
        add = add+m[i]
        # print("->",add)
        i += 1  
        
    mean1=add/len(m)
    return mean1

a_mean=MEAN1(a)
def Std1(m):
    Std1= []
    j = 0
    add=0
    while j < len(m):
        num = (m[j]-a_mean)**2
        add=add+num
        j = j+1
        
    newlen=len(m)-1
    std1=add/newlen
    return std1
std11=Std1(a)
std11

std11=2202172740.7636366

#7.2 计算小误差概率P
S0=0.6745*std11
S0

1485365513.645073

#7.3 计算绝对误差序列的标准差S2
import math
def MEAN2(m,n):
    add =0
    i = 0
    while i < len(m):
        num = abs(m[i]-n[i])
        add = add+num
        i += 1  
        
    mean2=add/len(m)
    return mean2
G_mean=MEAN2(a,G)
G_mean

def Std2(m):
    diff=[]
    b=[]
    j = 0
    add=0
    while j < len(m):
        a=abs(m[j]-G_mean)
        diff.append(a)
        num = diff[j]**2
        add=add+num
        
        b.append(diff[j]-S0)#有结果得知，所有e1都小于S0，所以小误差概率P=1
        
        j = j+1
        
    print("e1=",diff) 
    print("b=",b)
    newlen=len(m)-1
    std2=add/newlen
    return std2
std22=Std2(G)
std22

e1= [476474.47338380484, 46132.68916792523, 490606.9599327752, 518866.84394330514, 533290.41398843, 511783.53340697574, 533724.455532664, 548614.8638376463, 556609.6449682182, 480648.62113381556, 442272.51877881406]
b= [-1484889039.171689, -1485319380.955905, -1484874906.6851401, -1484846646.8011296, -1484832223.2310846, -1484853730.111666, -1484831789.1895404, -1484816898.7812352, -1484808904.0001047, -1484884865.0239391, -1484923241.1262941]

260767762838.65634

#7.4 计算方差比C
C=std11/std22
C#C小于0.35，又由7.3知，小误差概率P=1，所以模型有好的预测精度

0.008444957753946668