徐亦达 概率模型学习 ： hmm

引出： 条件概率 理解为 一对应无限 的函数 上的一个自变量点的情况

$p(x|y)$是有多种解释的 或者 是隐含了具体应用情况的，

以下将条件概率分布$p(x|y)$解释为

以一　对应　无穷 的函数
且
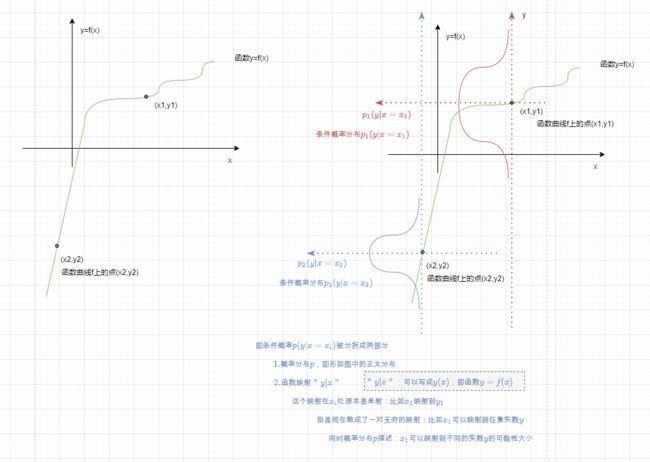
给任意某一对(x,y)一个数值来描述其可能性

(该可能性即概率，该可能性实际上是描述该x对应到该y却不对应到其他y的程度)

函数映射一般是单射或有限射, y=f(x) : 一个x只能对应有限个y，这才是函数（一个x对应多个y 可以用分段函数来表达， 但是总不能写无限个分段来表达无限吧）；
但是如果y=f(x)中 一个x对应了无穷多个y，应该用什么来描述？ 比如x=a点对应了无穷多个y，如何表达？就用$p(y|x=a)$这样一个条件概率分布来表达。由此可见条件概率分布是对函数的扩展和弥补。

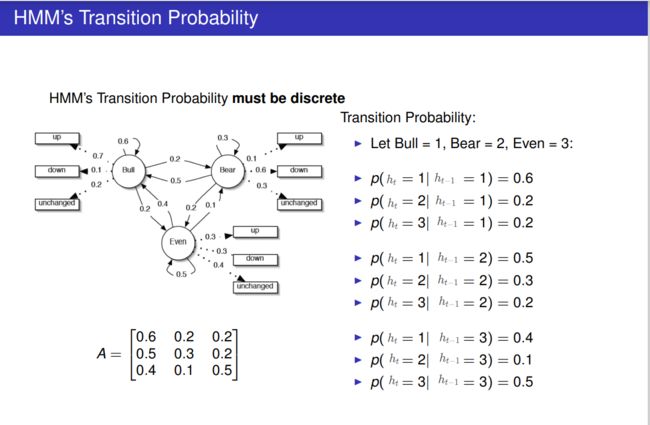
以下HMM中隐状态转移概率$p(h_t|h_{t-1}=b)$表达的其实就是在$h_{t-1}=b$点的 一对应无穷 的函数f： $q_t=f(h_{t-1})$， 所以条件概率的条件部分$h_{t-1}$其实相当于函数f的自变量 而条件概率的随机变量部分$h_t$其实相当于函数f的应变量
在这里准确的描述是： 条件概率分布$p(h_t|h_{t-1}=b)$可以描述 　一对应无穷 的函数f： $h_t=f(h_{t-1})$ 　　在 自变量的一个点$h_{t-1}=b$处 　　应变量$h_t$取哪些值及各取值的可能性

注意　上图我做过修改 ，
在原图中：　$q_i$是 随机变量 （隐变量）， 1、2、3是 该随机变量 的取值
而这里： $h_i$ 是 随机变量（隐变量） ， 1、2、3依然是 该随机变量 的取值
本文后续部分： $h_i$ 是 随机变量（隐变量） ， 而 $s_i$ 是 该随机变量 的取值 ; 即 $q_i$ -> $h_i$，1、2、3 -> $s_i$

条件概率 理解为 一对应无限 的函数 上的一个自变量点的情况

$p(x,y)=p(x|y)p(y)$ ；条件概率定义
$p(x,y)=p(x(y),y)=p(x|y)p(y)$ ；上式条件概率定义 式子 是把x当成了y的 一对应无限 的函数：x=x(y), y是自变量，x是应变量
需要考虑的问题是，假如x并不是y的函数呢？
上式其实隐含了 ：

p(x(y)) 其实是 p(x|y)的另一个写法而已； p(x(z), y(z)) 其实是 p(x,y|z)的另一个写法而已；
即 ： “x(y)” 即 “x|y” ， “x(z), y(z)” 即 “x,y|z”

插入自由变量式：
$p(y)={\Sigma }_{x}p(y,x)$ ； x是任意一个自由变量， x取遍所有x能取的值；

条件下插入自由变量式：
$p(y(z))={\Sigma }_{x(z)}p(y(z),x(z))$ ； 如果x、y均是z的 一对应无限 的函数: x=x(z), y=y(z) ， 依然有类似 “插入自由变量式” 的式子
上式子可以写作： $p(y|z)={\Sigma }_{x}p(y,x|z)$

条件概率画图

hmm

变量用词说明

以 h表示隐状态随机变量,
$h_1$即时刻1的隐状态随机变量 ,
$h_2$即时刻2的隐状态随机变量 ,
…
$h_n$即时刻n的隐状态随机变量 ,

以$s_1,s_2,...,s_k$表示k个隐状态的取值

$h_i$可以取$s_1,s_2,...,s_k$中的任意一个值

如何表示$p(y_1,y_2)$, 答案是：
$p(y_1,y_2)={\Sigma }_{h_1=q_1}^{q_k}{\Sigma }_{h_2=q_1}^{q_k}(p(y_2|h_2)p(y_1|h_1)p(h_2|h_1)p(h_1))$； 推导过程如下：

；推导$p(y_1)$：
$p(y_1)={\Sigma }_{h_1=s_1}^{s_k}p(y_1,h_1)={\Sigma }_{h_1=s_1}^{s_k}p(y_1(h_1),h_1)={\Sigma }_{h_1=s_1}^{s_k}(p(y_1|h_1)p(h_1))$ ; 即：
$p(y_1)={\Sigma }_{h_1=s_1}^{s_k}(p(y_1|h_1)p(h_1))$
“推导$p(y_1)$” 在 “推导$p(y_1,y_2)$” 中并没有被直接用到，这里只是写在这而已

；推导$p(y_1,y_2)$:
；在 $p(y_1,y_2)$ 中插入自由变量$h_2$，得：
$p(y_1,y_2)={\Sigma }_{h_2=s_1}^{s_k}p(y_1(h_2),y_2(h_2),h_2)$；再插入自由变量$h_1$，得：
$p(y_1,y_2)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}p(y_1(h_1,h_2),y_2(h_1,h_2),h_2(h_1),h_1)$；抽出$h_1$，得：
$p(y_1,y_2)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}(p(y_1(h_2),y_2(h_2),h_2|h_1)p(h_1))$；再抽出$h_2$，得：
$p(y_1,y_2)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}(p(y_1,y_2|h_2,h_1)p(h_2|h_1)p(h_1))$；将$y_2$当成$y_2(y_1)$ ，得:
$p(y_1,y_2)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}(p(y_1,y_2(y_1)|h_2,h_1)p(h_2|h_1)p(h_1))$；抽出$y_1$，得：
$p(y_1,y_2)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}(p(y_2|h_2,h_1,y_1)p(y_1|h_2,h_1)p(h_2|h_1)p(h_1))$ ；根据hmm假设，有 “$y_2|y_1,h_1,h_2$” 即 “$y_2|h_2$” ，有 “$y_1|h_1,h_2$” 即 “$y_1|h_1$” ：
$p(y_1,y_2)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}(p(y_2|h_2)p(y_1|h_1)p(h_2|h_1)p(h_1))$ ；这里每一项都是hmm已知的；

；推导$p(y_1,y_2,y_3)$:
；在 $p(y_1,y_2,y_3)$ 中 插入自由变量$h_3$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_3=s_1}^{s_k}p(y_1(h_3),y_2(h_3),y_3(h_3),h_3)$；插入自由变量$h_2$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}p(y_1(h_2,h_3),y_2(h_2,h_3),y_3(h_2,h_3),h_3(h_2),h_2)$；插入自由变量$h_1$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}p(y_1(h_1,h_2,h_3),y_2(h_1,h_2,h_3),y_3(h_1,h_2,h_3),h_3(h_1,h_2),h_2(h_1),h_1)$；抽出$h_1$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_1(h_2,h_3),y_2(h_2,h_3),y_3(h_2,h_3),h_3(h_2),h_2|h_1)p(h_1))$；抽出$h_2$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_1(h_3),y_2(h_3),y_3(h_3),h_3|h_2,h_1)p(h_2|h_1)p(h_1))$；抽出$h_3$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_1,y_2,y_3|h_3,h_2,h_1)p(h_3|h_2,h_1)p(h_2|h_1)p(h_1))$；将 $y_3$当成$y_3(y_1)$ ，$y_2$当成$y_2(y_1)$ 得:
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_1,y_2(y_1),y_3(y_1)|h_3,h_2,h_1)p(h_3|h_2,h_1)p(h_2|h_1)p(h_1))$；抽出$y_1$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_2,y_3|y_1,h_3,h_2,h_1)p(y_1|h_3,h_2,h_1)p(h_3|h_2,h_1)p(h_2|h_1)p(h_1))$；将$y_3$当成$y_3(y_2)$ ，得:
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_2,y_3(y_2)|y_1,h_3,h_2,h_1)p(y_1|h_3,h_2,h_1)p(h_3|h_2,h_1)p(h_2|h_1)p(h_1))$；抽出$y_2$，得：
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_3|y_2,y_1,h_3,h_2,h_1)p(y_2|y_1,h_3,h_2,h_1)p(y_1|h_3,h_2,h_1)p(h_3|h_2,h_1)p(h_2|h_1)p(h_1))$；根据hmm假设 ：
$p(y_1,y_2,y_3)={\Sigma }_{h_1=s_1}^{s_k}{\Sigma }_{h_2=s_1}^{s_k}{\Sigma }_{h_3=s_1}^{s_k}(p(y_3|h_3)p(y_2|h_2)p(y_1|h_1)p(h_3|h_2)p(h_2|h_1)p(h_1))$；这里每一项都是hmm已知的；

垃圾箱：
$p(y_1,y_2)={\Sigma }_{h_1=q_1}^{q_k}{\Sigma }_{h_2=q_1}^{q_k}p(y_1(h_1,h_2),y_2(h_1,h_2),h_1,h_2)$； 忽略
$p(y_1,y_2)={\Sigma }_{h_1=q_1}^{q_k}{\Sigma }_{h_2=q_1}^{q_k}(p(y_1,y_2|h_1,h_2)p(h_1,h_2))$； 忽略
$p(y_1,y_2)={\Sigma }_{h_1=q_1}^{q_k}p(y_1,y_2|h_1)p(h_1)$； 忽略

那么 请问 $p(y|\theta )$ 也是相当于 $p(y(\theta ))$ 吗？

问： $p(y|\theta )$ 也是相当于 $p(y(\theta ))$ ？
答： 是

目前所知道的 :

在 训练一个概率模型 的 过程中， 模型的参数 $\theta$ 是变化的 , 即 $\theta$是变量 ，此时 $p(y|\theta )$ 有讨论价值 。 $p(y|\theta )$ 相当于 $p(y(\theta ))$
即在训练过程中， $p(y|\theta )$ 相当于 $p(y(\theta ))$ 且 其中的 $\theta$不可省略 （因$\theta$是变量）

当 模型训练完后 使用该模型 时， $\theta$ 是 不变的，即$\theta$是常量， 此时 $p(y|\theta )$ 也相当于 $p(y(\theta ))$。 很显然 $y(\theta )$中的$\theta$是自变量，而此时该自变量$\theta$是不变的 因此 该自变量$\theta$可以省略。
即在验证或测试过程中， $p(y|\theta )$ 也相当于 $p(y(\theta ))$ 但 其中的 $\theta$可省略 （因$\theta$是常量）