YOLOv3算法原理以及paddle实现

YOLOv3算法原理以及paddle实现

根据paddle零基础入门课整理的YOLOv3学习笔记。

1. 概述

经典的R-CNN系列算法也被称为两阶段目标检测算法，由于这种方法需要先产生候选区域，再对候选区域做分类和位置坐标的预测，因此算法速度非常慢。与此对应的是以YOLO算法为代表的单阶段检测算法，只需要一个网络即可同时产生候选区域并预测出物体的类别和位置坐标。

与R-CNN系列算法不同，YOLOv3使用单个网络结构，在产生候选区域的同时即可预测出物体类别和位置，不需要分成两阶段来完成检测任务。另外，YOLOv3算法产生的预测框数目比Faster R-CNN少很多。Faster R-CNN中每个真实框可能对应多个标签为正的候选区域，而YOLOv3里面每个真实框只对应一个正的候选区域。这些特性使得YOLOv3算法具有更快的速度，能到达实时响应的水平。

Joseph Redmon等人在2015年提出YOLO（You Only Look Once，YOLO）算法，通常也被称为YOLOv1；2016年，他们对算法进行改进，又提出YOLOv2版本；2018年发展出YOLOv3版本。

2. YOLOv3模型设计思想

• 在训练阶段：

1. 按一定规则在图片上产生一系列的候选区域，然后根据这些候选区域与图片上物体真实框之间的位置关系对候选区域进行标注。跟真实框足够接近的那些候选区域会被标注为正样本，同时将真实框的位置作为正样本的位置目标。偏离真实框较大的那些候选区域则会被标注为负样本，负样本不需要预测位置或者类别。
2. 使用卷积神经网络提取图片特征并对候选区域的位置和类别进行预测。这样每个预测框就可以看成是一个样本，根据真实框相对它的位置和类别进行了标注而获得标签值，通过网络模型预测其位置和类别，将网络预测值和标签值进行比较，就可以建立起损失函数。

• 在预测阶段，根据预先定义的锚框和提取到的图片特征计算预测框，然后使用多分类非极大值抑制消除重合较大的框，得到最终结果。

YOLOv3的算法流程如 图1 所示。

图1：目标检测设计方案

接下来，分别从训练和预测两个维度对YOLOv3算法进行深入了解。

3. YOLOv3模型训练

YOLOv3算法的训练流程可以分成两部分，如 图2 所示。

• 按一定规则在图片上产生一系列的候选区域，然后根据这些候选区域与图片上物体真实框之间的位置关系对候选区域进行标注。跟真实框足够接近的那些候选区域会被标注为正样本，同时将真实框的位置作为正样本的位置目标。偏离真实框较大的那些候选区域则会被标注为负样本，负样本不需要预测位置或者类别。
• 使用卷积神经网络提取图片特征并对候选区域的位置和类别进行预测。这样每个预测框就可以看成是一个样本，根据真实框相对它的位置和类别进行了标注而获得标签值，通过网络模型预测其位置和类别，将网络预测值和标签值进行比较，就可以建立起损失函数。

图2：YOLOv3算法训练流程图

• 图2 左边是输入图片，上半部分所示的过程是使用卷积神经网络对图片提取特征，随着网络不断向前传播，特征图的尺寸越来越小，每个像素点会代表更加抽象的特征模式，直到输出特征图，其尺寸减小为原图的$\frac{1}{32}$。
• 图2 下半部分描述了生成候选区域的过程，首先将原图划分成多个小方块，每个小方块的大小是$32\times 32$，然后以每个小方块为中心分别生成一系列锚框，整张图片都会被锚框覆盖到。在每个锚框的基础上产生一个与之对应的预测框，根据锚框和预测框与图片上物体真实框之间的位置关系，对这些预测框进行标注。
• 将上方支路中输出的特征图与下方支路中产生的预测框标签建立关联，创建损失函数，开启端到端的训练过程。

接下来具体介绍流程中各节点的算法原理。

3.1 产生候选区域

如何产生候选区域，是检测模型的核心设计方案。目前大多数基于卷积神经网络的模型所采用的方式大体如下：

1. 按一定的规则在图片上生成一系列位置固定的锚框，将这些锚框看作是可能的候选区域。
2. 对锚框是否包含目标物体进行预测，如果包含目标物体，还需要预测所包含物体的类别，以及预测框相对于锚框位置需要调整的幅度。

1. 生成锚框

在YOLOv3算法中，将原始图片划分成$m\times n$个区域，如 图3 所示，原始图片高度$H=640$, 宽度$W=480$，如果我们选择小块区域的尺寸为$32\times 32$，则$m$和$n$分别为：

$$m=\frac{640}{32}=20$$

$$n=\frac{480}{32}=15$$

也就是说，我们将原始图像分成了20行15列小方块区域。

图3：将图片划分成多个32x32的小方块

YOLOv3算法会在每个区域的中心，生成一系列锚框。为了展示方便，我们仅在图中第十行第四列的小方块位置附近画出生成的锚框，如 图4 所示。

图4：在第10行第4列的小方块区域生成3个锚框

---

说明：

这里为了跟程序中的编号对应，最上面的行号是第0行，最左边的列号是第0列。

---

2. 生成预测框

在前面已经指出，锚框的位置都是固定好的，不可能刚好跟物体边界框重合，需要在锚框的基础上进行位置的微调以生成预测框。预测框相对于锚框会有不同的中心位置和大小，采用什么方式能得到预测框呢？我们先来考虑如何生成其中心位置坐标。

比如上面图中在第10行第4列的小方块区域中心生成的一个锚框，如绿色虚线框所示。以小方格的宽度为单位长度，

此小方块区域左上角的位置坐标是：
$$c_x=4$$
$$c_y=10$$

此锚框的区域中心坐标是：
$$center\_x=c_x+0.5=4.5$$
$$center\_y=c_y+0.5=10.5$$

可以通过下面的方式生成预测框的中心坐标：
$$b_x=c_x+\sigma (t_x)$$
$$b_y=c_y+\sigma (t_y)$$

其中$t_x$和$t_y$为实数，$\sigma (x)$是我们之前学过的Sigmoid函数，其定义如下：

$$\sigma (x)=\frac{1}{1+exp(-x)}$$

由于Sigmoid的函数值在$0\sim 1$之间，因此由上面公式计算出来的预测框的中心点总是落在第十行第四列的小区域内部。

当$t_x=t_y=0$时，$b_x=c_x+0.5$，$b_y=c_y+0.5$，预测框中心与锚框中心重合，都是小区域的中心。

锚框的大小是预先设定好的，在模型中可以当作是超参数，下图中画出的锚框尺寸是

$$p_h=350$$
$$p_w=250$$

此时，可以通过下面的公式生成预测框的大小：

$$b_h=p_h{e}^{t_h}$$
$$b_w=p_w{e}^{t_w}$$

如果$t_x=t_y=0,t_h=t_w=0$，则预测框跟锚框重合。

如果给$t_x,t_y,t_h,t_w$随机赋值如下：

$$t_x=0.2,t_y=0.3,t_w=0.1,t_h=-0.12$$

则可以得到预测框的坐标是(154.98, 357.44, 276.29, 310.42)，如 图5 中蓝色框所示。

图5：生成预测框

---

说明：
这里坐标采用$xywh$的格式。

---

这里我们会问：当$t_x,t_y,t_w,t_h$取值为多少的时候，预测框能够跟真实框重合？为了回答问题，只需要将上面预测框坐标中的$b_x,b_y,b_h,b_w$设置为真实框的位置，即可求解出$t$的数值。

令：
$$\sigma (t_x^{\ast })+c_x=g{t}_x$$
$$\sigma (t_y^{\ast })+c_y=g{t}_y$$
$$p_w{e}^{t_w^{\ast }}=g{t}_h$$
$$p_h{e}^{t_h^{\ast }}=g{t}_w$$

可以求解出：$(t_x^{\ast },t_y^{\ast },t_w^{\ast },t_h^{\ast })$

如果$t$是网络预测的输出值，将$t^{\ast }$作为目标值，以他们之间的差距作为损失函数，则可以建立起一个回归问题，通过学习网络参数，使得$t$足够接近$t^{\ast }$，从而能够求解出预测框的位置坐标和大小。

预测框可以看作是在锚框基础上的一个微调，每个锚框会有一个跟它对应的预测框，我们需要确定上面计算式中的$t_x,t_y,t_w,t_h$，从而计算出与锚框对应的预测框的位置和形状。

3. 对候选区域进行标注

在YOLOv3中，每个区域会产生3种不同形状的锚框，每个锚框都是一个可能的候选区域，对这些候选区域我们需要了解如下几件事情：

• 锚框是否包含物体，这可以看成是一个二分类问题，使用标签objectness来表示。当锚框包含了物体时，objectness=1，表示预测框属于正类；当锚框不包含物体时，设置objectness=0，表示锚框属于负类；还有一种情况，有些预测框跟真实框之间的IoU很大，但并不是最大的那个，那么直接将其objectness标签设置为0当作负样本，可能并不妥当，为了避免这种情况，YOLOv3算法设置了一个IoU阈值iou_threshold，当预测框的objectness不为1，但是其与某个真实框的IoU大于iou_threshold时，就将其objectness标签设置为-1，不参与损失函数的计算。

• 如果锚框包含了物体，那么就需要计算对应的预测框中心位置和大小应该是多少，或者说上文中的$t_x,t_y,t_w,t_h$应该是多少。

• 如果锚框包含了物体，那么就需要计算具体类别是什么，这里使用变量label来表示其所属类别的标签。

标注锚框中是否包含物体

如 图6 所示，这里一共有3个目标，以最左边的人像为例，其真实框是$(133.96,328.42,186.06,374.63)$。

图6：选出与真实框中心位于同一区域的锚框

真实框的中心点坐标是：

$$center\_x=133.96$$

$$center\_y=328.42$$

$$i=133.96/32=4.18625$$

$$j=328.42/32=10.263125$$

它落在了第10行第4列的小方块内，如图13所示。此小方块区域可以生成3个不同形状的锚框，其在图上的编号和大小分别是$A_1(116,90),A_2(156,198),A_3(373,326)$。

用这3个不同形状的锚框跟真实框计算IoU，选出IoU最大的锚框。这里为了简化计算，只考虑锚框的形状，不考虑其跟真实框中心之间的偏移，具体计算结果如 图7 所示。

图7：选出与真实框与锚框的IoU

其中跟真实框IoU最大的是锚框$A_3$，形状是$(373,326)$，将它所对应的预测框的objectness标签设置为1，其所包括的物体类别就是真实框里面的物体所属类别。

依次可以找出其他几个真实框对应的IoU最大的锚框，然后将它们的预测框的objectness标签也都设置为1。这里一共有$20\times 15\times 3=900$个锚框，只有3个预测框会被标注为正。

由于每个真实框只对应一个objectness标签为正的预测框，如果有些预测框跟真实框之间的IoU很大，但并不是最大的那个，那么直接将其objectness标签设置为0当作负样本，可能并不妥当。为了避免这种情况，YOLOv3算法设置了一个IoU阈值iou_threshold，当预测框的objectness不为1，但是其与某个真实框的IoU大于iou_threshold时，就将其objectness标签设置为-1，不参与损失函数的计算。

所有其他的预测框，其objectness标签均设置为0，表示负类。

对于objectness=1的预测框，需要进一步确定其位置和包含物体的具体分类标签，但是对于objectness=0或者-1的预测框，则不用管他们的位置和类别。

标注预测框位置大小

当锚框objectness=1时，需要确定预测框位置相对于它微调的幅度，也就是锚框的位置标签。

在前面我们已经问过这样一个问题：当$t_x,t_y,t_w,t_h$取值为多少的时候，预测框能够跟真实框重合？其做法是将预测框坐标中的$b_x,b_y,b_h,b_w$设置为真实框的坐标，即可求解出$t$的数值。

令：
$$\sigma (t_x^{\ast })+c_x=g{t}_x$$
$$\sigma (t_y^{\ast })+c_y=g{t}_y$$
$$p_w{e}^{t_w^{\ast }}=g{t}_w$$
$$p_h{e}^{t_h^{\ast }}=g{t}_h$$

对于$t_x^{\ast }$和$t_y^{\ast }$，由于Sigmoid的反函数不好计算，我们直接使用$\sigma (t_x^{\ast })$和$\sigma (t_y^{\ast })$作为回归的目标。

$$d_x^{\ast }=\sigma (t_x^{\ast })=g{t}_x-c_x$$

$$d_y^{\ast }=\sigma (t_y^{\ast })=g{t}_y-c_y$$

$$t_w^{\ast }=log(\frac{g{t}_w}{p_w})$$

$$t_h^{\ast }=log(\frac{g{t}_h}{p_h})$$

如果$(t_x,t_y,t_h,t_w)$是网络预测的输出值，将$(d_x^{\ast },d_y^{\ast },t_w^{\ast },t_h^{\ast })$作为$(\sigma (t_x),\sigma (t_y),t_h,t_w)$的目标值，以它们之间的差距作为损失函数，则可以建立起一个回归问题，通过学习网络参数，使得$t$足够接近$t^{\ast }$，从而能够求解出预测框的位置。

标注锚框中物体类别

对于objectness=1的锚框，需要确定其具体类别。正如上面所说，objectness标注为1的锚框，会有一个真实框跟它对应，该锚框所属物体类别，即是其所对应的真实框包含的物体类别。这里使用one-hot向量来表示类别标签label。比如一共有10个分类，而真实框里面包含的物体类别是第2类，则label为$(0,1,0,0,0,0,0,0,0,0)$

总结起来，如 图8 所示。

图8：标注流程示意图

通过上述介绍，我们初步了解了YOLOv3中候选区域的标注方式，通过这种方式，我们就可以获取到真实的预测框标签。在 Paddle 中，这些操作都已经被封装到了 paddle.vision.ops.yolo_loss API中，计算损失时，只需要调用这个API即可简单实现上述过程。接下来，我们再了解一下YOLOv3的网络结构，看网络是如何计算得到对应的预测值的。

3.2 YOLOv3 网络结构

1. backbone

YOLOv3算法使用的骨干网络是Darknet53。Darknet53网络的具体结构如 图9 所示，在ImageNet图像分类任务上取得了很好的成绩。在检测任务中，将图中C0后面的平均池化、全连接层和Softmax去掉，保留从输入到C0部分的网络结构，作为检测模型的基础网络结构，也称为骨干网络。YOLOv3模型会在骨干网络的基础上，再添加检测相关的网络模块。

图9：Darknet53网络结构

下面的程序是Darknet53骨干网络的实现代码，这里将上图中C0、C1、C2所表示的输出数据取出，并查看它们的形状分别是，$C0[1,1024,20,20]$，$C1[1,512,40,40]$，$C2[1,256,80,80]$。

# coding=utf-8
# 导入环境
import os
import random
import xml.etree.ElementTree as ET
import numpy as np
import matplotlib.pyplot as plt
# 在notebook中使用matplotlib.pyplot绘图时，需要添加该命令进行显示
%matplotlib inline
from matplotlib.image import imread
import matplotlib.patches as patches
import cv2
from PIL import Image, ImageEnhance
import paddle
import paddle.nn.functional as F


# 将卷积和批归一化封装为ConvBNLayer，方便后续复用
class ConvBNLayer(paddle.nn.Layer):
    def __init__(self, ch_in, ch_out,  kernel_size=3, stride=1, groups=1, padding=0, act="leaky"):
        # 初始化函数
        super(ConvBNLayer, self).__init__()
        # 创建卷积层
        self.conv = paddle.nn.Conv2D(in_channels=ch_in, out_channels=ch_out, kernel_size=kernel_size, stride=stride, padding=padding, 
            groups=groups, weight_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Normal(0., 0.02)), bias_attr=False)
        # 创建批归一化层
        self.batch_norm = paddle.nn.BatchNorm2D(num_features=ch_out,
            weight_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Normal(0., 0.02), regularizer=paddle.regularizer.L2Decay(0.)),
            bias_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Constant(0.0), regularizer=paddle.regularizer.L2Decay(0.)))
        self.act = act

    def forward(self, inputs):
        # 前向计算
        out = self.conv(inputs)
        out = self.batch_norm(out)
        if self.act == 'leaky':
            out = F.leaky_relu(x=out, negative_slope=0.1)
        return out

# 定义下采样模块，使图片尺寸减半
class DownSample(paddle.nn.Layer):
    def __init__(self, ch_in, ch_out, kernel_size=3, stride=2, padding=1):
        # 初始化函数
        super(DownSample, self).__init__()
        # 使用 stride=2 的卷积，可以使图片尺寸减半
        self.conv_bn_layer = ConvBNLayer(ch_in=ch_in, ch_out=ch_out, kernel_size=kernel_size, stride=stride, padding=padding)
        self.ch_out = ch_out
        
    def forward(self, inputs):
        # 前向计算
        out = self.conv_bn_layer(inputs)
        return out

# 定义残差块
class BasicBlock(paddle.nn.Layer):
    def __init__(self, ch_in, ch_out):
        # 初始化函数
        super(BasicBlock, self).__init__()
        # 定义两个卷积层
        self.conv1 = ConvBNLayer(ch_in=ch_in, ch_out=ch_out, kernel_size=1, stride=1, padding=0)
        self.conv2 = ConvBNLayer(ch_in=ch_out, ch_out=ch_out*2, kernel_size=3, stride=1, padding=1)
        
    def forward(self, inputs):
        # 前向计算
        conv1 = self.conv1(inputs)
        conv2 = self.conv2(conv1)
        # 将第二个卷积层的输出和最初的输入值相加
        out = paddle.add(x=inputs, y=conv2)
        return out

# 将多个残差块封装为一个层级，方便后续复用
class LayerWarp(paddle.nn.Layer):
    def __init__(self, ch_in, ch_out, count, is_test=True):
        # 初始化函数
        super(LayerWarp,self).__init__()
        self.basicblock0 = BasicBlock(ch_in, ch_out)
        self.res_out_list = []
        for i in range(1, count):
            # 使用add_sublayer添加子层
            res_out = self.add_sublayer("basic_block_%d" % (i), BasicBlock(ch_out*2, ch_out))
            self.res_out_list.append(res_out)

    def forward(self,inputs):
        # 前向计算
        y = self.basicblock0(inputs)
        for basic_block_i in self.res_out_list:
            y = basic_block_i(y)
        return y

# DarkNet 每组残差块的个数，来自DarkNet的网络结构图
DarkNet_cfg = {53: ([1, 2, 8, 8, 4])}
# 创建DarkNet53骨干网络
class DarkNet53_conv_body(paddle.nn.Layer):
    def __init__(self):
        # 初始化函数
        super(DarkNet53_conv_body, self).__init__()
        self.stages = DarkNet_cfg[53]
        self.stages = self.stages[0:5]

        # 第一层卷积
        self.conv0 = ConvBNLayer(ch_in=3, ch_out=32, kernel_size=3, stride=1, padding=1)

        # 下采样，使用stride=2的卷积来实现
        self.downsample0 = DownSample(ch_in=32, ch_out=32 * 2)

        # 添加各个层级的实现
        self.darknet53_conv_block_list = []
        self.downsample_list = []
        for i, stage in enumerate(self.stages):
            conv_block = self.add_sublayer("stage_%d" % (i), LayerWarp(32*(2**(i+1)), 32*(2**i), stage))
            self.darknet53_conv_block_list.append(conv_block)
        # 两个层级之间使用DownSample将尺寸减半
        for i in range(len(self.stages) - 1):
            downsample = self.add_sublayer("stage_%d_downsample" % i, DownSample(ch_in=32*(2**(i+1)), ch_out=32*(2**(i+2))))
            self.downsample_list.append(downsample)

    def forward(self,inputs):
        # 前向计算
        out = self.conv0(inputs)
        out = self.downsample0(out)
        blocks = []
        # 依次将各个层级作用在输入上面
        for i, conv_block_i in enumerate(self.darknet53_conv_block_list): 
            out = conv_block_i(out)
            blocks.append(out)
            if i < len(self.stages) - 1:
                out = self.downsample_list[i](out)
        # 将C0, C1, C2作为返回值
        return blocks[-1:-4:-1] 

2. 预测模块

上文中，我们了解到在YOLOv3算法中，网络需要输出3组结果，分别是：

• 预测框是否包含物体。也可理解为 objectness=1 的概率是多少，这里可以让网络输出一个实数 $x$ ，然后用 $Sigmoid(x)$ 表示 objectness 为正的概率 $P_{obj}$ 。

• 预测物体位置和形状。可以用网络输出4个实数来表示物体位置和形状 $t_x,t_y,t_w,t_h$ 。

• 预测物体类别。预测图像中物体的具体类别是什么，或者说其属于每个类别的概率分别是多少。总的类别数为 C ，需要预测物体属于每个类别的概率 $(P_1,P_2,...,P_C)$ ，可以用网络输出C个实数 $(x_1,x_2,...,x_C)$ ，对每个实数分别求 Sigmoid 函数，让 $P_i=Sigmoid(x_i)$ ，则可以表示出物体属于每个类别的概率。

因此，对于一个预测框，网络需要输出 $(5+C)$ 个实数来表征它是否包含物体、位置和形状尺寸以及属于每个类别的概率。

由于我们在每个小方块区域都生成了 3 个预测框，则所有预测框一共需要网络输出的预测值数目是：

$$[3\times (5+C)]\times m\times n$$

还有更重要的一点是网络输出必须要能区分出小方块区域的位置来，不能直接将特征图连接一个输出大小为 $[3\times (5+C)]\times m\times n$ 的全连接层。

这里继续使用上文中的图片，现在观察特征图，经过多次卷积核池化之后，其步幅 stride=32，$640\times 480$ 大小的输入图片变成了 $20\times 15$ 的特征图；而小方块区域的数目正好是$20\times 15$，也就是说可以让特征图上每个像素点分别跟原图上一个小方块区域对应。这也是为什么我们最开始将小方块区域的尺寸设置为32的原因，这样可以巧妙的将小方块区域跟特征图上的像素点对应起来，解决了空间位置的对应关系。

图10：特征图C0与小方块区域形状对比

下面还需要将像素点$(i,j)$与第i行第j列的小方块区域所需要的预测值关联起来，每个小方块区域产生3个预测框，每个预测框需要$(5+C)$个实数预测值，则每个像素点相对应的要有$3\times (5+C)$个实数。为了解决这一问题，对特征图进行多次卷积，并将最终的输出通道数设置为$3\times (5+C)$，即可将生成的特征图与每个预测框所需要的预测值巧妙的对应起来。经过卷积后，保证输出的特征图尺寸变为$[1,75,20,15]$。每个小方块区域生成的锚框或者预测框的数量是3，物体类别数目是20，每个区域需要的预测值个数是$3\times (5+20)=75$，正好等于输出的通道数。

此时，输出特征图与候选区域关联方式如 图11 所示。

将$P0[t,0:25,i,j]$与输入的第t张图片上小方块区域$(i,j)$第1个预测框所需要的25个预测值对应，$P0[t,25:50,i,j]$与输入的第t张图片上小方块区域$(i,j)$第2个预测框所需要的25个预测值对应，$P0[t,50:75,i,j]$与输入的第t张图片上小方块区域$(i,j)$第3个预测框所需要的25个预测值对应。

$P0[t,0:4,i,j]$与输入的第t张图片上小方块区域$(i,j)$第1个预测框的位置对应，$P0[t,4,i,j]$与输入的第t张图片上小方块区域$(i,j)$第1个预测框的objectness对应，$P0[t,5:25,i,j]$与输入的第t张图片上小方块区域$(i,j)$第1个预测框的类别对应。

通过这种方式可以巧妙的将网络输出特征图，与每个小方块区域生成的预测框对应起来了。

图11：特征图P0与候选区域的关联

骨干网络的输出特征图是C0，下面的程序是对C0进行多次卷积以得到跟预测框相关的特征图P0。

class YoloDetectionBlock(paddle.nn.Layer):
    # define YOLOv3 detection head
    # 使用多层卷积和BN提取特征
    def __init__(self,ch_in,ch_out,is_test=True):
        super(YoloDetectionBlock, self).__init__()

        assert ch_out % 2 == 0, \
            "channel {} cannot be divided by 2".format(ch_out)

        self.conv0 = ConvBNLayer(ch_in=ch_in, ch_out=ch_out, kernel_size=1, stride=1, padding=0)
        self.conv1 = ConvBNLayer(ch_in=ch_out, ch_out=ch_out*2, kernel_size=3, stride=1, padding=1)
        self.conv2 = ConvBNLayer(ch_in=ch_out*2, ch_out=ch_out, kernel_size=1, stride=1, padding=0)
        self.conv3 = ConvBNLayer(ch_in=ch_out, ch_out=ch_out*2, kernel_size=3, stride=1, padding=1)
        self.route = ConvBNLayer(ch_in=ch_out*2, ch_out=ch_out, kernel_size=1, stride=1, padding=0)
        self.tip = ConvBNLayer(ch_in=ch_out, ch_out=ch_out*2, kernel_size=3, stride=1, padding=1)
        
    def forward(self, inputs):
        out = self.conv0(inputs)
        out = self.conv1(out)
        out = self.conv2(out)
        out = self.conv3(out)
        route = self.route(out)
        tip = self.tip(route)
        return route, tip

3. 多尺度检测

上文中我们讲解的运算过程都是在特征图P0的基础上进行的，它的步幅stride=32。特征图的尺寸比较小，像素点数目比较少，每个像素点的感受野很大，具有非常丰富的高层级语义信息，可能比较容易检测到较大的目标。为了能够检测到尺寸较小的那些目标，需要在尺寸较大的特征图上面建立预测输出。如果我们在C2或者C1这种层级的特征图上直接产生预测输出，可能面临新的问题，它们没有经过充分的特征提取，像素点包含的语义信息不够丰富，有可能难以提取到有效的特征模式。在目标检测中，解决这一问题的方式是，将高层级的特征图尺寸放大之后跟低层级的特征图进行融合，得到的新特征图既能包含丰富的语义信息，又具有较多的像素点，能够描述更加精细的结构。

具体的网络实现方式如 图12 所示：

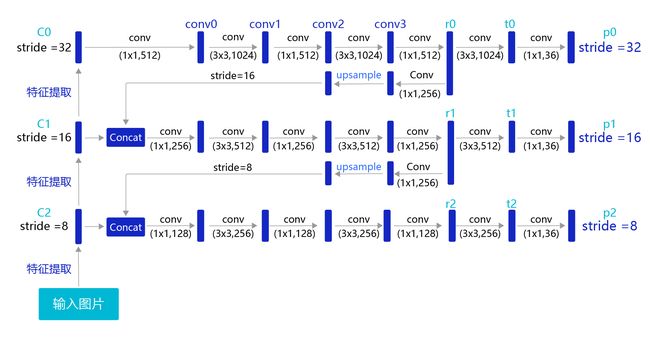
图12：生成多层级的输出特征图P0、P1、P2

YOLOv3在每个区域的中心位置产生3个锚框，在3个层级的特征图上产生锚框的大小分别为P2 [(10×13),(16×30),(33×23)]，P1 [(30×61),(62×45),(59× 119)]，P0[(116 × 90), (156 × 198), (373 × 326]。越往后的特征图上用到的锚框尺寸也越大，能捕捉到大尺寸目标的信息；越往前的特征图上锚框尺寸越小，能捕捉到小尺寸目标的信息。

所以，最终的损失函数计算以及模型预测都是在这3个层级上进行的。接下来就可以进行完整网络结构的定义了。

---

说明：

YOLOv3中，损失函数主要包括3个部分，分别是：

• 表征是否包含目标物体的损失函数，使用二值交叉熵损失函数进行计算。

• 表征物体位置的损失函数，其中，$t_x,t_y$ 使用二值交叉熵损失函数进行计算，$t_w,t_h$ 使用L1损失进行计算。

• 表征物体类别的损失函数，使用二值交叉熵损失函数进行计算。

---

3.3 端到端训练

YOLOv3的训练过程如 图13 所示，输入图片经过特征提取得到三个层级的输出特征图P0(stride=32)、P1(stride=16)和P2(stride=8)，相应的分别使用不同大小的小方块区域去生成对应的锚框和预测框，并对这些锚框进行标注。

• P0层级特征图，对应着使用$32\times 32$大小的小方块，在每个区域中心生成大小分别为$[116,90]$, $[156,198]$, $[373,326]$的三种锚框。

• P1层级特征图，对应着使用$16\times 16$大小的小方块，在每个区域中心生成大小分别为$[30,61]$, $[62,45]$, $[59,119]$的三种锚框。

• P2层级特征图，对应着使用$8\times 8$大小的小方块，在每个区域中心生成大小分别为$[10,13]$, $[16,30]$, $[33,23]$的三种锚框。

将三个层级的特征图与对应锚框之间的标签关联起来，并建立损失函数，总的损失函数等于三个层级的损失函数相加。通过极小化损失函数，可以开启端到端的训练过程。

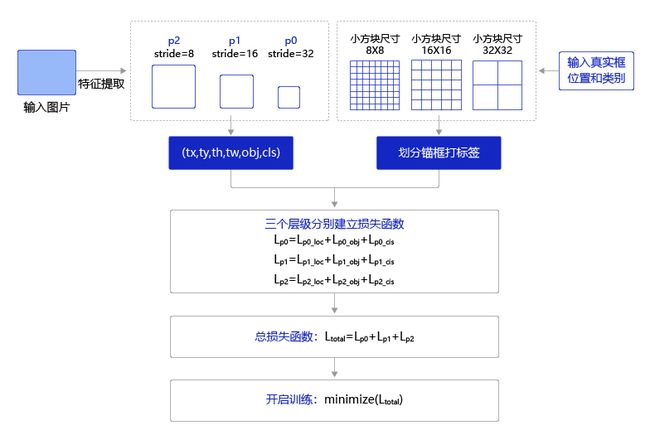
图13：端到端训练流程

在完整网络定义时，我们需要使用 paddle.vision.ops.yolo_loss API来计算损失函数，该API 将上述候选区域的标注以及多尺度的损失函数计算统一地进行了封装。

paddle.vision.ops.yolo_loss(x, gt_box, gt_label, anchors, anchor_mask, class_num, ignore_thresh, downsample_ratio, gt_score=None, use_label_smooth=True, name=None, scale_x_y=1.0)

关键参数说明如下：

• x: 输出特征图。
• gt_box: 真实框。
• gt_label: 真实框标签。
• ignore_thresh，预测框与真实框IoU阈值超过ignore_thresh时，不作为负样本，YOLOv3模型里设置为0.7。
• downsample_ratio，特征图P0的下采样比例，使用Darknet53骨干网络时为32。
• gt_score，真实框的置信度，在使用了mixup技巧时用到。
• use_label_smooth，一种训练技巧，如不使用，设置为False。
• name，该层的名字，比如’yolov3_loss’，默认值为None，一般无需设置。

4. YOLOv3模型预测

预测过程流程 图14 如下所示：

图14：预测流程

预测过程可以分为两步：

1. 通过网络输出计算出预测框位置和所属类别的得分。
2. 使用非极大值抑制来消除重叠较大的预测框。

4.1 预测框计算

我们可以使用paddle.vision.ops.yolo_box来计算三个层级的特征图对应的预测框和得分。

paddle.vision.ops.yolo_box(x, img_size, anchors, class_num, conf_thresh, downsample_ratio, clip_bbox=True, name=None, scale_x_y=1.0)

关键参数含义如下：

• x，网络输出特征图，例如上面提到的P0或者P1、P2。
• img_size，输入图片尺寸。
• anchors，使用到的anchor的尺寸，如[10, 13, 16, 30, 33, 23, 30, 61, 62, 45, 59, 119, 116, 90, 156, 198, 373, 326]
• anchor_mask: 每个层级上使用的anchor的掩码，[[6, 7, 8], [3, 4, 5], [0, 1, 2]]
• class_num，物体类别数。
• conf_thresh, 置信度阈值，得分低于该阈值的预测框位置数值不用计算直接设置为0.0。
• downsample_ratio, 特征图的下采样比例，例如P0是32，P1是16，P2是8。
• name=None，名字，例如’yolo_box’，一般无需设置，默认值为None。

返回值包括两项，boxes和scores，其中boxes是所有预测框的坐标值，scores是所有预测框的得分。

预测框得分的定义是所属类别的概率乘以其预测框是否包含目标物体的objectness概率，即

$$score=P_{obj}\cdot P_{classification}$$

通过调用paddle.vision.ops.yolo_box获得P0、P1、P2三个层级的特征图对应的预测框和得分，并将他们拼接在一块，即可得到所有的预测框及其属于各个类别的得分。

至此，完整的YOLOv3网络就可以被定义出来了，完整代码如下：

# 定义上采样模块
class Upsample(paddle.nn.Layer):
    def __init__(self, scale=2):
        # 初始化函数
        super(Upsample,self).__init__()
        self.scale = scale

    def forward(self, inputs):
        # 前向计算
        # 获得动态的上采样输出形状
        shape_nchw = paddle.shape(inputs)
        shape_hw = paddle.slice(shape_nchw, axes=[0], starts=[2], ends=[4])
        shape_hw.stop_gradient = True
        in_shape = paddle.cast(shape_hw, dtype='int32')
        out_shape = in_shape * self.scale
        out_shape.stop_gradient = True

        # 上采样计算
        out = paddle.nn.functional.interpolate(x=inputs, scale_factor=self.scale, mode="NEAREST")
        return out

# 定义完整的YOLOv3模型
class YOLOv3(paddle.nn.Layer):
    def __init__(self, num_classes=20):
        # 初始化函数
        super(YOLOv3,self).__init__()

        self.num_classes = num_classes
        # 提取图像特征的骨干代码
        self.block = DarkNet53_conv_body()
        self.block_outputs = []
        self.yolo_blocks = []
        self.route_blocks_2 = []
        # 生成3个层级的特征图P0, P1, P2
        for i in range(3):
            # 添加从ci生成ri和ti的模块
            yolo_block = self.add_sublayer("yolo_detecton_block_%d" % (i),
                YoloDetectionBlock(ch_in=512//(2**i)*2 if i==0 else 512//(2**i)*2 + 512//(2**i), ch_out = 512//(2**i)))
            self.yolo_blocks.append(yolo_block)

            num_filters = 3 * (self.num_classes + 5)

            # 添加从ti生成pi的模块，这是一个Conv2D操作，输出通道数为3 * (num_classes + 5)
            block_out = self.add_sublayer("block_out_%d" % (i),
                paddle.nn.Conv2D(in_channels=512//(2**i)*2, out_channels=num_filters, kernel_size=1, stride=1, padding=0,
                       weight_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Normal(0., 0.02)),
                       bias_attr=paddle.ParamAttr(initializer=paddle.nn.initializer.Constant(0.0), regularizer=paddle.regularizer.L2Decay(0.))))
            self.block_outputs.append(block_out)
            if i < 2:
                # 对ri进行卷积
                route = self.add_sublayer("route2_%d"%i, ConvBNLayer(ch_in=512//(2**i), ch_out=256//(2**i), kernel_size=1, stride=1, padding=0))
                self.route_blocks_2.append(route)
            # 将ri放大以便跟c_{i+1}保持同样的尺寸
            self.upsample = Upsample()

    def forward(self, inputs):
        # 前向运算
        outputs = []
        blocks = self.block(inputs)
        for i, block in enumerate(blocks):
            if i > 0:
                # 将r_{i-1}经过卷积和上采样之后得到特征图，与这一级的ci进行拼接
                block = paddle.concat([route, block], axis=1)
            # 从ci生成ti和ri
            route, tip = self.yolo_blocks[i](block)
            # 从ti生成pi
            block_out = self.block_outputs[i](tip)
            # 将pi放入列表
            outputs.append(block_out)

            if i < 2:
                # 对ri进行卷积调整通道数
                route = self.route_blocks_2[i](route)
                # 对ri进行放大，使其尺寸和c_{i+1}保持一致
                route = self.upsample(route)

        return outputs

    def get_loss(self, outputs, gtbox, gtlabel, gtscore=None, anchors = [10, 13, 16, 30, 33, 23, 30, 61, 62, 45, 59, 119, 116, 90, 156, 198, 373, 326],
                 anchor_masks = [[6, 7, 8], [3, 4, 5], [0, 1, 2]], ignore_thresh=0.7, use_label_smooth=False):
        # 损失计算函数
        self.losses = []
        downsample = 32
        # 对三个层级分别求损失函数
        for i, out in enumerate(outputs): 
            anchor_mask_i = anchor_masks[i]
            # 使用paddle.vision.ops.yolo_loss 直接计算损失函数
            loss = paddle.vision.ops.yolo_loss(x=out, gt_box=gtbox, gt_label=gtlabel, gt_score=gtscore, anchors=anchors, anchor_mask=anchor_mask_i, 
                    class_num=self.num_classes, ignore_thresh=ignore_thresh, downsample_ratio=downsample, use_label_smooth=False)
            self.losses.append(paddle.mean(loss)) 
            # 下一级特征图的缩放倍数会减半
            downsample = downsample // 2 
        # 对所有层级求和
        return sum(self.losses) 

    def get_pred(self, outputs, im_shape=None, anchors = [10, 13, 16, 30, 33, 23, 30, 61, 62, 45, 59, 119, 116, 90, 156, 198, 373, 326],
                 anchor_masks = [[6, 7, 8], [3, 4, 5], [0, 1, 2]], valid_thresh = 0.01):
        # 预测函数
        downsample = 32
        total_boxes = []
        total_scores = []
        for i, out in enumerate(outputs):
            anchor_mask = anchor_masks[i]
            anchors_this_level = []
            for m in anchor_mask:
                anchors_this_level.append(anchors[2 * m])
                anchors_this_level.append(anchors[2 * m + 1])
            # 使用paddle.vision.ops.yolo_box 直接计算损失函数
            boxes, scores = paddle.vision.ops.yolo_box(x=out, img_size=im_shape, anchors=anchors_this_level, class_num=self.num_classes,
                   conf_thresh=valid_thresh, downsample_ratio=downsample, name="yolo_box" + str(i))
            total_boxes.append(boxes)
            total_scores.append(paddle.transpose( scores, perm=[0, 2, 1]))
            downsample = downsample // 2
        # 将三个层级的结果进行拼接
        yolo_boxes = paddle.concat(total_boxes, axis=1)
        yolo_scores = paddle.concat(total_scores, axis=2)
        return yolo_boxes, yolo_scores

4.2 多分类极大值抑制

在前边的计算过程中，网络对同一个目标可能会进行多次检测。这也就导致对于同一个物体，预测会产生多个预测框。因此，得到模型输出后，需要使用非极大值抑制（non-maximum suppression, nms）来消除冗余框。基本思想是，如果有多个预测框都对应同一个物体，则只选出得分最高的那个预测框，剩下的预测框被丢弃掉。

如何判断两个预测框对应的是同一个物体呢，标准该怎么设置？

如果两个预测框的类别一样，而且他们的位置重合度比较大，则可以认为他们是在预测同一个目标。非极大值抑制的做法是，选出某个类别得分最高的预测框，然后看哪些预测框跟它的IoU大于阈值，就把这些预测框给丢弃掉。这里IoU的阈值是超参数，需要提前设置，YOLOv3模型里面设置的是0.5。

计算IOU的代码如下所示。

# 计算IoU，其中边界框的坐标形式为xyxy
def box_iou_xyxy(box1, box2):
    # 获取box1左上角和右下角的坐标
    x1min, y1min, x1max, y1max = box1[0], box1[1], box1[2], box1[3]
    # 计算box1的面积
    s1 = (y1max - y1min + 1.) * (x1max - x1min + 1.)
    # 获取box2左上角和右下角的坐标
    x2min, y2min, x2max, y2max = box2[0], box2[1], box2[2], box2[3]
    # 计算box2的面积
    s2 = (y2max - y2min + 1.) * (x2max - x2min + 1.)
    
    # 计算相交矩形框的坐标
    xmin = np.maximum(x1min, x2min)
    ymin = np.maximum(y1min, y2min)
    xmax = np.minimum(x1max, x2max)
    ymax = np.minimum(y1max, y2max)
    # 计算相交矩形行的高度、宽度、面积
    inter_h = np.maximum(ymax - ymin + 1., 0.)
    inter_w = np.maximum(xmax - xmin + 1., 0.)
    intersection = inter_h * inter_w
    # 计算相并面积
    union = s1 + s2 - intersection
    # 计算交并比
    iou = intersection / union
    return iou

非极大值抑制的具体实现代码如下面的nms函数的定义，需要说明的是数据集中含有多个类别的物体，所以这里需要做多分类非极大值抑制，其实现原理与非极大值抑制相同，区别在于需要对每个类别都做非极大值抑制，实现代码如下面的multiclass_nms所示。

# 非极大值抑制
def nms(bboxes, scores, score_thresh, nms_thresh):
    # 对预测框得分进行排序
    inds = np.argsort(scores)
    inds = inds[::-1]
    keep_inds = []
    # 循环遍历预测框
    while(len(inds) > 0):
        cur_ind = inds[0]
        cur_score = scores[cur_ind]
        # 如果预测框得分低于阈值，则退出循环
        if cur_score < score_thresh:
            break
        # 计算当前预测框与保留列表中的预测框IOU，如果小于阈值则保留该预测框，否则丢弃该预测框
        keep = True
        for ind in keep_inds:
            current_box = bboxes[cur_ind]
            remain_box = bboxes[ind]
            # 计算当前预测框与保留列表中的预测框IOU
            iou = box_iou_xyxy(current_box, remain_box)
            if iou > nms_thresh:
                keep = False
                break
        if keep:
            keep_inds.append(cur_ind)
        inds = inds[1:]
    return np.array(keep_inds)

# 多分类非极大值抑制
def multiclass_nms(bboxes, scores, score_thresh=0.01, nms_thresh=0.45, pos_nms_topk=100):
    batch_size = bboxes.shape[0]
    class_num = scores.shape[1]
    rets = []
    for i in range(batch_size):
        bboxes_i = bboxes[i]
        scores_i = scores[i]
        ret = []
        # 遍历所有类别进行单分类非极大值抑制
        for c in range(class_num):
            scores_i_c = scores_i[c]
            # 单分类非极大值抑制
            keep_inds = nms(bboxes_i, scores_i_c, score_thresh, nms_thresh)
            if len(keep_inds) < 1:
                continue
            keep_bboxes = bboxes_i[keep_inds]
            keep_scores = scores_i_c[keep_inds]
            keep_results = np.zeros([keep_scores.shape[0], 6])
            keep_results[:, 0] = c
            keep_results[:, 1] = keep_scores[:]
            keep_results[:, 2:6] = keep_bboxes[:, :]
            ret.append(keep_results)
        if len(ret) < 1:
            rets.append(ret)
            continue
        ret_i = np.concatenate(ret, axis=0)
        scores_i = ret_i[:, 1]
        # 如果保留的预测框超过100个，只保留得分最高的100个
        if len(scores_i) > pos_nms_topk:
            inds = np.argsort(scores_i)[::-1]
            inds = inds[:pos_nms_topk]
            ret_i = ret_i[inds]
        rets.append(ret_i)
    return rets