字符串相关
哈希
Hash,一般翻译做散列、杂凑,或音译为哈希,是把任意长度的输入(又叫做预映射)通过散列算法变换成固定长度的输出,该输出就是散列值。这种转换是一种压缩映射,也就是,散列值的空间通常远小于输入的空间,不同的输入可能会散列成相同的输出,所以不可能从散列值来确定唯一的输入值。简单的说就是一种将任意长度的消息压缩到某一固定长度的消息摘要的函数。
有m个字符串,总长S。q次询问两个字符串是否完全一样。数据范围10^5。
一个相对普适的做法是这样的:
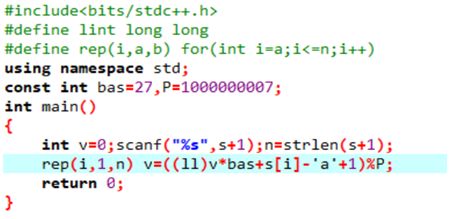
将这个字符串(假设只有小写字母)视为一个27进制数,将a看作1,b看作2,依此类推。
比如‘abca’看作1*27^3+2*27^2+3*27+1。
但这样在字符串较大时数字会很大,存不下来。
一个欺骗方法是找一个较大的数P(最好是大质数),只记录转换后数字对P取模的结果。
注意
不能把a看作0,否则’a’和’aa’相同。
取的bas要和P互质,否则bas的指数足够大时模P就=0,那一位就没用了。(gcd(bas,P)=1)(gcd最大公约数)
补充
自然溢出
由于哈希涉及大量取模,所以有可能有常数问题,实践中可以用自然溢出代替,即采用unsigned long long类型运算,相当于自动对2^64取模,同时还能提高正确率。
但可以被构造卡,需慎重。
哈希冲突
由于bas的缘故,可以想象两个字符串有相同的哈希值很困难。
可以证明这么做出问题(即哈希值相等但是字符串不同)的概率是O(1/sqrt(p))的,一般情况下够用了。
但是有些时候可能会有问题(错误概率不够小),可以通过找两组bas和P来解决(双哈希)。
生日悖论
生日悖论是指在不少于 23 个人中至少有两人生日相同的概率大于 50%。从引起逻辑矛盾的角度来说,生日悖论是一种 “佯谬”。但这个数学事实十分反直觉,故称之为一个悖论。生日悖论的数学理论被应用于设计密码学攻击方法——生日攻击。
生日悖论普遍的应用于检测哈希函数:N 位长度的哈希表可能发生碰撞测试次数不是 2N 次而是只有 2N/2 次。这一结论被应用到破解密码哈希函数的 “生日攻击” 中。
相关题目
子串哈希值提取
(pre:前缀)
子串可视为前缀的后缀/后缀的前缀。
给定一个长位n字符串s,q次询问两个子串s1和s2是否相同。
拓展一下刚刚的哈希算法。
考虑对字符串的每个前缀计算其哈希值:
![]()
那么对于子串[l, r],可知其哈希值可用以下式子计算(计算方式可能不同)。
哈分加二希 哈希加二分
给一个字符串 S,多次询问两个后缀的最长公共前缀(LCP)。
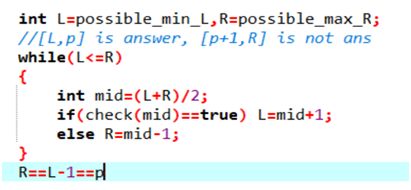
推荐的二分写法
哈希与回文串
给一个长为n的串s,q次询问一个子串是否是回文串。
回文串就是从左往右读和从右往左读,结果一样的串。
那么正着做一遍哈希,倒着读做一遍哈希,提取两遍子串哈希值即可。
KMP算法
KMP算法的核心是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的。
前置知识
border指所有那些既是前缀又是后缀,但不是本身的串。
border的border仍是border。
一个串的所有border互为border。
若Lborder为一个串的最长border,那么border的Lborder,Lborder的Lborder……为这个串的所有border。
所以实际上每个前缀都指向自己的最长border(没有则指向超级根),可以形成一个树形结构,每个点到根的路径就是所有border。
T-c是S-c的border(c是一个字符),那么T是S的border。(反过来不一定成立)
换句话说,S-c的Lborder一定是S的一个border增加一个字符得到的(注意这里没有L)
怎么对S的每个前缀求Lborder?
假设我们求出了S的所有前缀的Lborder,那么按照刚刚的性质从长到短暴力枚举S的所有border T,找到第一个使得T后面字符是c即可。
方便起见,记S[l:r]表示S从第l个字符到第r个字符形成的子串。
首先S[1:1]的Lborder是0。
从i=2,…,n,假设已经求除了S[1:1],…,S[1:(i-1)]的Lborder,现在要求S[1:i]的Lborder,根据刚才的讨论,只要枚举S[1:(i-1)]的border即可,即令j=Lborder[i-1],然后不停的令j=Lborder[j],直到j=0或者S[j+1]==S[i]为止。
显然Lborder[i]<=Lborder[i-1]+1,而每一轮j跳跃次数不超过|Lborder[i]-Lborder[i-1]|,由于总有Lborder[i]>=0,所以Lborder变小的幅度之和不会超过变大的幅度之和,而变大的幅度之和显然是O(n)的,因此复杂度线性。
每个border都与一个不严格循环节一一对应。
也就是说,如果m是长为n的字符串S的一个border,那么m-n就是S的一个不严格循环节,反之亦然。因此找到一个串的所有不严格循环节,只要枚举一个串的所有border即可。而(严格的)循环节就是那些使得(m-n)|n的长为m的border。
Manacher算法
Manacher算法,又叫“马拉车”算法,可以在时间复杂度为O(n)的情况下求解一个字符串的最长回文子串长度的问题。
在进行Manacher算法时,字符串都会进行上面的进入一个字符处理,比如输入的字符为acbbcbds,用“#”字符处理之后的新字符串就是#a#c#b#b#c#b#d#s#。
Trie树
在计算机科学中,trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
在Trie上,两个字符串的最长公共前缀(LCP)就是两个点LCA(最近公共祖先)所对应的点。
有些时候,我们也可以将数字看作一个二进制数,或者输一个由0/1组成的定长字符串,来解决一些问题。
AC自动机
考虑一个KMP的EX版本。
给定一个模板串T,和若干匹配串S1~Sm,对每个Si询问其在T中出现几次。|T|<=100000,Si总长<=100000。
考虑把S放到一块建类似nxt一样的东西(在AC自动机中叫fail指针) 。
先将S建Trie,考虑在Trie上运行T。
当遇到无法匹配的情况时,希望找到T已匹配部分的一个最长后缀,使得这个后缀也是某个S的前缀。注意这里实际上和T无关,我们只需要对Trie上每个节点对应的字符串做这件事情即可。
换句话说,我们要对每个点找到其最长后缀也是某个S的前缀,而S的前缀必然对应Trie上一个点,或者说我们需要找到一个失配节点(fail)。
具体的找法用一个bfs就能实现。
除了一些特殊情况,一个点的fail,就是其fail的fail的对应子节点(如果有的话)。没有的话就继续跳fail。
可以证明这样做的复杂度是正确的。
匹配T的时候,就用T在S上面跑,每次失配就沿着fail指针向上跳直到可以继续匹配为止。
这样复杂度显然是线性的。
注意问题
一个点对应字符串出现次数需要统计子树和,比如abcd对应节点被出现一次,那么bcd,cd,d都要出现一次。
直接如此实现会有常数上的劣势,一个显著的改进方法是:一个点的ch[c]等于其对应儿子,若该点有c的出边;否则这个点的ch[c]=发生失配时最终转移到的点。
只需要在求fail的时候,对于第二种情况(假设当前是x)ch[x][c]=ch[fail[fa[x]]][c]即可,注意特判根节点周围的一圈点。
这样能显著优化常数,而且在做另一些问题是能简化问题。
给n个串然后两两询问的题有些时候的处理方法
考虑选一个适当大小的数字s,那么一个串长度要么不超过s,而长度超过s的只有不超过m/s个。
若询问两个长度均不超过s的串,那么直接KMP即可,复杂度O(s);
若询问中有至少一个串长度超过s,假设是A,那么用AC自动机预处理所有串在A中出现了几次,复杂度是O(m)的,由于这部分A只有不超过m/s,所以这部分预处理复杂度O(m^2/s)。
因此总复杂度O(qs+m^2/s)。取s=sqrt(m^2/q)时有最小值O(m*sqrt(q))。
不过大多数题m,q同阶,所以偷懒取s=sqrt(m)也行。具体取多少还可以适当调参来加速(因为两部分算法有常数差异)
后缀数组SA
SA能在O(nlgn)时间内将所有后缀按照字典序排序,然后求排名相邻的两个后缀的LCP(最长公共前缀),结果就是得到了排序后的结果。。
一个简单的推论是,两个后缀的LCP就是后缀数组对应位次间所有相邻字符串LCP的最小值,这样可以RMQ(区间最值查询)。
可以利用SA求一个字符串有多少本质不同的子串(即长的不一样),或者求一个字符串的第k小等。
这些问题本质相同:
考虑如何按从小到大的顺序得到s的所有子串。
由于子串就是后缀的前缀,所有我们只需要考察所有后缀的前缀即可。
从小到大考虑SA中的后缀,假设考虑到了第i个,和第i-1小的后缀的LCP是L,那么第i小的后缀的长小于等于L的前缀都是已经考虑过的,而长大于L的前缀都是新出现且字典序逐渐增大的子串。
那么这两个问题解决了。
第二个问题通过二分可以O(lgn)回答。
同理也可以求一个子串的位次,方法是先找到所在后缀,对应到SA上,考虑二分出一个最小的以这个子串为前缀的后缀(即两个后缀的LCP长度大于等于子串长度),然后求一下现在这个后缀和前一个后缀的LCP即可算出该子串的位次。
因此可以用SA实现子串和位次的转化。
同时参照上面的方法也可以求出一个子串在哪些位置出现过。
SAM(后缀自动机)
SAM就是将DFA与后缀结合,将重复的后缀压缩成只有一个,这样剩下了空间。
但是后缀自动机厉害的地方就是空间时间都是线性复杂度的,十分优秀。
SAM的每个状态st都包含了一部分S的子串,记作substrings(st),并且对于两个不同状态u和v,包含的子串substrings(u) ∩ substrings(v) = ∅; (2)每个子串都恰好被一个状态包含。所以我们只要构造出来S对应的SAM,再对所有状态st求Σ(maxlen(st)-minlen(st))就是子串的数目。
回文自动机
同其他自动机一样,回文自动机是个DAG(有向无环图),它用相当少(O(n))的空间复杂度就存储了这个字符串的所有回文串信息。一个回文自动机包含不超过|S|个节点,每个节点都表示了这个字符串的一个不重复的回文子串,同时一个节点会有不超过字符集大小的边连向其他节点,以及一条fail边连向这个点的fail......
和别的自动机不太一样,回文自动机是有两棵树的森林:其中一棵是长度为偶数的回文串集合,另一棵是长度为奇数的回文串集合,这两棵树的根节点分别表示长度为0(空串)和-1(无实际含义,便于运算)的回文串。
自动机中每条有向边都有一个字符类型的权值,起点的串左右分别加上这个字符得到的就是终点的串。举个例子:设一条边权为c的边连接的两个点分别是A,B,A表示回文串aba,则B表示的回文串就是cabac 。特别的,如果A是那个长度为−1的根,B串就是这条边的权值。
当你插入一个字符的时候,插入的点代表的就是这个字符匹配的最长回文串,也就是说从根节点往下顺着边走,记着一个str一开始为空,一边走一边不停地往str左右两边添加新的字符,走到一个点,这个点代表的回文串就是str。
每个点都有个fail边,这条边指向这个点所代表的回文串的 最长回文后缀所在的那个点(最长回文后缀:串中满足回文的最长的后缀,这个串自己不算)如果没有,则指向0(就是那个根节点)。特别的,0的fail节点就是那个长度为-1的点。
后缀树
后缀树是一种数据结构,能快速解决很多关于字符串的问题。一个string S的后缀树是一个边被标记为字符串的树。因此每一个S的后缀都唯一对应一条从根节点到叶节点的路径。这样就形成了一个S的后缀的基数树。后缀树是前缀树里的一个特殊类型
SA-IS
SA−IS排序是基于诱导排序这种思想,将问题规模缩小,解决更小的问题,快速解决原问题的算法。
补充
递推
递推算法是一种用若干步可重复运算来描述复杂问题的方法。递推是序列计算中的一种常用算法。通常是通过计算前面的一些项来得出序列中的指定项的值。
递推是按照一定的规律来计算序列中的每个项,通常是通过计算前面的一些项来得出序列中的指定项的值。其思想是把一个复杂的庞大的计算过程转化为简单过程的多次重复,该算法利用了计算机速度快和不知疲倦的机器特点。
代码技巧
除了打暴力不要用string,用char s[1000];
下标从1开始的方法:
![]()
n=strlen(s+1);
如果读入m个字符串,总长<=10^5但是每个字符串的长度不能保证,可以类似如下方式避免动态指针:
如果你不会指针,那就只能用一个st[i]表示第i个字符串是从s中哪一位开始的了。
*a→获得a的地址。
并非原创,仅是整理,请见谅