Paper Information
论文作者:Zhen Peng、Wenbing Huang、Minnan Luo、Q. Zheng、Yu Rong、Tingyang Xu、Junzhou Huang
论文来源:WWW 2020
论文地址:download
代码地址:download
前言
1、自监督学习(Self-supervised):属于无监督学习,其核心是自动为数据打标签(伪标签或其他角度的可信标签,包括图像的旋转、分块等等),通过让网络按照既定的规则,对数据打出正确的标签来更好地进行特征表示,从而应用于各种下游任务。
2、互信息(Mutual Information):表示两个变量 $X$ 和 $Y$ 之间的关系,定义为:
$I(X ; Y)=\sum\limits_{x \in X} \sum\limits _{y \in Y} p(x, y) \log \frac{p(x \mid y)}{p(x)}$
可以解释为由 $X$ 引入而使 $Y$ 的不确定度减小的量, $I(X ; Y) $ 越大说明两者关系越密切。
3、噪声对抗估计 (Noise Contrastive Estimation, NCE) :在 NLP 任务中一种降低计算复杂度的 方法,将语言模型估计问题简化为一个二分类问题。
Abstract
本文研究了如何以无监督的方式将图形结构数据中的丰富信息保存并提取到嵌入空间中。
Graphical Mutual Information (GMI) 用于测量输入图和高级隐藏表示之间的相关性。
在 GMI 的帮助下,我们开发了一个无监督的学习模型,通过最大化图神经编码器的输入和输出之间的 GMI 来进行训练。
1 Introduction
Deep Graph Infomax (DGI) ,通过最大化图级别表示向量和隐藏表示互信息之间的互信息【全局和局部信息之间的互信息】,来区分 Positive graph 和 Negative graph 。其存在的问题是:获取图级别表示的 Readout 函数常常是单设的,但是 Readout 的单设性能会受到参数训练方式的影响,这表明 Readout 函数在某些情况下会变成非单射。当 Readout 函数非单射时,图表示中包含的输入图信息将随着输入图的大小增大而减小【一对多造成】。
接着,本文提出了一种直接的方法来考虑图结构方面的 $\text{MI}$,而不使用任何 Readout 函数和 corruption function,作者通过比较编码器的输入(即由输入邻域组成的子图)和输出(即每个节点的隐藏表示),直接推导出 $\text{MI}$。[ 改进 ]
作者理论推导表明,直接导出的 $\text{MI}$ 可以分解为每个邻居特征和隐藏向量之间的局部 $\text{MI}$ 的加权和。这样,我们对输入特征进行了分解,使 $\text{MI}$ 计算易于处理。此外,如果我们调整权值,这种形式的 $\text{MI}$ 可以很容易地满足对称性质。由于上述 $\text{MI}$ 主要是在节点特征级别上测量的,作者称之为特征互信息(FMI)。
关于上述提到的 $\text{FMI}$ ,存在着两个问题:
-
- 组合的权重仍然未知;
- 没有考虑到拓扑结构(即边缘特性);
为解决这两个问题,作者定义了基于 $\text{FMI}$ 提出了 Graphical Mutual Information(GMI),GMI 将 $\text{FMI}$ 中的权重设置为表示空间中每个邻居和目标节点之间的距离。为了保留拓扑信息,GMI 通过一个额外的互信息项进一步将这些权值与输入的边缘特征相关联。
2 Related work
2.1 Mutual information estimation
如 1995 年的 InfoMax原则一样,主张最大化神经网络的输入和输出之间的 $\text{MI}$。
论文参考类型 1、2。
2.2 Neural networks for graph representation learning
论文参考类型3、4、5、6。
3 Graphical mutual information:definition and maximization
图$\mathcal{G}$:$\mathcal{G}=\{\mathcal{V}, \mathcal{E}\}$ , $v_{i} \in \mathcal{V} $, $e_{i j}=\left(v_{i}, v_{j}\right) \in \mathcal{E}$
假设节点特征服从经验概率分布 $ \mathbb{P}$ ,由 $\boldsymbol{X} \in \mathbb{R}^{N \times D}=\left\{\boldsymbol{x}_{1}, \ldots, \boldsymbol{x}_{N}\right\}$ 给出,其中 $\boldsymbol{x}_{i} \in \mathbb{R}^{D}$ 表示节点 $v_{i}$ 的特征。
邻接矩阵 $\boldsymbol{A} \in \mathbb{R}^{N \times N}$ 表示连接关系 ,与边 $e_{i j}$ 对应的 $A_{i j}$ 可以是实数,也可以是多维向量。
图表示学习目标是根据输入的特征矩阵和邻接矩阵学习一个能获得潜在表示的编码器 $f: \mathbb{R}^{N \times D} \times \mathbb{R}^{N \times N} \rightarrow \mathbb{R}^{N \times D^{\prime}} $ ,这样潜在向量 $\boldsymbol{H}=\left\{\boldsymbol{h}_{1}, \cdots, \boldsymbol{h}_{N}\right\}=f(\boldsymbol{X}, \boldsymbol{A})$ 表示所有节点的高阶表示。
那么承接Introduction 中提到的 [ 改进 ] ,编码过程可以在节点级重写。作者将节点 $i$ 的 $\boldsymbol{X}_{i}$ 和 $\boldsymbol{A}_{i}$ 分别定义为其邻居的特征矩阵和对应邻接矩阵。特别地,当编码器 $f$ 是 $l$ 层 GNN 时, $\boldsymbol{X}_{i}$ 由 $v_{i}$ 的所有 $k \leq l$ $\text{hop}$ 邻居组成,显然还可以进一步在邻接矩阵中添加自环,那么它则会包含节点 $i$ 本身信息。图中节点编码过程: $\boldsymbol{h}_{i}=f\left(\mathcal{G}_{i}\right)=f\left(\boldsymbol{X}_{i}, \boldsymbol{A}_{i}\right)$ 。
Difficulties in defining graphical mutual information
根据 Deep InfoMax(DIM)的思想,应该最大化每个节点的表示 $\boldsymbol{h}_{i}$ 和 $\mathcal{G}_{i}$ 之间的 $\text{MI}$,这里用 $\text{MI}$表示为 $I\left(\boldsymbol{h}_{i} ; \mathcal{G}_{i}\right)$ 。但是,没有一个较好的方法定义 $I\left(\boldsymbol{h}_{i} ; \mathcal{G}_{i}\right)$ ,原因是:
-
- $\text{MI}$ 应该具有平移不变性,即:如果 $\mathcal{G}_{i}$ 和 $\mathcal{G}_{i}^{\prime}$ 同构,那么 $I\left(\boldsymbol{h}_{i} ; \mathcal{G}_{i}\right)=I\left(\boldsymbol{h}_{i} ; \mathcal{G}_{i}^{\prime}\right)$ 。
- 如果采用 MINE 方法进行 $\text{ML}$ 计算,那么 MINE 中的判别器只接受固定大小的输入。但这对于 $\mathcal{G}_{i}$ 是不可行的,因为不同的 $\mathcal{G}_{i}$ 通常包含不同数量的邻居节点,因此具有不同的大小。
3.1 Feature Mutual Information
将 $\boldsymbol{X}_{i}$ 的经验概率分布表示为 $p\left(\boldsymbol{X}_{i}\right)$, $\boldsymbol{h}_{i} $ 的概率分布表示为 $p\left(\boldsymbol{h}_{i}\right)$ ,联合分布用 $p\left(\boldsymbol{h}_{i}, \boldsymbol{X}_{i}\right) $ 表示。 根据信息论,$\boldsymbol{h}_{i} $ 和 $\boldsymbol{X}_{i}$ 之间的 $\text{MI}$ 可以定义为:
${\large I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right)=\int_{\mathcal{H}} \int_{\mathcal{X}} p\left(\boldsymbol{h}_{i}, \boldsymbol{X}_{i}\right) \log \frac{p\left(\boldsymbol{h}_{i}, \boldsymbol{X}_{i}\right)}{p\left(\boldsymbol{h}_{i}\right) p\left(\boldsymbol{X}_{i}\right)} d \boldsymbol{h}_{i} d \boldsymbol{X}_{i}}\quad\quad\quad(1) $
以下将根据互信息分解定理计算 $I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right)$。
Theorem 1 (Mutual information decomposition). If the conditional probability $p\left(\boldsymbol{h}_{i} \mid \boldsymbol{X}_{i}\right)$ is multiplicative, the global mutual information $I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right)$ defined in Eq. (1) can be decomposed as a weighted sum of local MIs, namely,
$I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right)=\sum\limits _{j}^{i_{n}} w_{i j} I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)\quad\quad\quad\quad(2)$
其中:
-
- $x_{j}$ is the $j-th$ neighbor of node $i$
- $i_{n}$ is the number of all elements in $X_{i}$
- the weight $w_{i j}$ satisfies $\frac{1}{i_{n}} \leq w_{i j} \leq 1$ for each $j$
为了证明 Theorem 1 ,我们首先引入了两个 lemmas 和一个 definition。
Lemma 1. For any random variables $X$, $Y$, and $Z$, we have
$I(X, Y ; Z) \quad \geq \quad I(X ; Z)\qquad \qquad (3)$
证明:
$\begin{array}{l}I(X, Y ; Z)-I(X ; Z)\\ =\iiint_{X Y Z} p(X, Y, Z) \log \frac{p(X, Y, Z)}{p(X, Y) p(Z)} d X d Y d Z-\iint_{X Z} p(X, Z) \log \frac{p(X, Z)}{p(X) p(Z)} d X d Z\\ =\iiint_{X Y Z} p(X, Y, Z) \log \frac{p(X, Y, Z)}{p(X, Y) p(Z)} d X d Y d Z-\iiint_{X Y Z} p(X, Y, Z) \log \frac{p(X, Z)}{p(X) p(Z)} d X d Y d Z\\ =\iiint_{XYZ} p(X, Y, Z) \log \frac{p(X, Y, Z)}{p(Y \mid X) p(X, Z)} d X d Y d Z\\ =\iiint_{XYZ} p(Y, Z \mid X) p(X) \log \frac{p(Y, Z \mid X)}{p(Y \mid X) p(Z \mid X)} d X d Y d Z\\ =I(Y ; Z \mid X) \geq 0 \end{array}$
因此,我们得到 $I(X,Y;Z) \ge I(X;Z)$。
Definition 1. The conditional probability $p\left(h \mid X_{1}, \cdots, X_{n}\right)$ is called multiplicative if it can be written as a product
$p\left(h \mid X_{1}, \cdots, X_{n}\right)=r_{1}\left(h, X_{1}\right) \cdots r_{n}\left(h, X_{n}\right)\quad\quad\quad\quad(4)$
其中 $r_1, · · · ,r_n$ 是 appropriate functions 。
Lemma 2. If $p\left(h \mid X_{1}, \cdots, X_{n}\right)$ is multiplicative, then we have
$I(X ; Z)+I(Y ; Z) \geq I(X, Y ; Z)\quad\quad\quad(5)$
现在来证明 Theorem 1 :
根据 Lemma 1 ,对于任何一个 $j$ :
$I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right)=I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{1}, \cdots, \boldsymbol{x}_{i_{n}}\right) \geq I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)\quad\quad\quad(6)$
这意味着:
$I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right)=\sum\limits \frac{1}{i_{n}} I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right) \geq \sum \limits \frac{1}{i_{n}} I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)\quad\quad\quad(7)$
另一方面,根据 Lemma 2 ,我们得到:
$I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right) \leq \sum\limits I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)\quad\quad\quad(8)$
根据 $\text{Eq.7}$ 和 $\text{Eq.8}$ :
$\sum\limits \frac{1}{i_{n}} I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right) \leq I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right) \leq \sum\limits I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)\quad\quad \quad(9)$
因为 $I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right) \geq 0$ ,必须存在权重 $\frac{1}{i_{n}} \leq w_{i j} \leq 1 $。 当设置 $w_{i j}=I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{i}\right) / \sum I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)$ 时,我们将实现 $\text{Eq.2}$,同时确保 $\frac{1}{i_{n}} \leq w_{i j} \leq 1$,进而证明了定理1。
利用 Theorem 1 中的分解,可以通过 MINE 计算出 $\text{Eq.2}$ 的右侧,因为鉴别器的输入现在成了 $\left(\boldsymbol{h}_{i}, \boldsymbol{x}_{j}\right) $ 对,它们的大小总是保持不变 (即 $D^{\prime}-b y-D$) 。
此外,我们还可以调整权值,以反映输入图的同构变换。例如,如果 $ \boldsymbol{X}_{i} $ 只包含节点 $ i $ 的 $1-h o p $ 邻居,则将所有权重设置为相同, 将导致不同顺序的输入节点产生相同的 $\mathrm{MI}$。
尽管分解有一些好处,但很难表征权值的确切值,因为它们与 $I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)$ 的值及其潜在的概率分布有关。
一种简单的方法是将所有权值设置为 $ \frac{1}{i_{n}} $ ,然后 $\text{Eq.2}$ 右边的最大化等价于最大化 $I\left(\boldsymbol{h}_{i} ; \boldsymbol{X}_{j}\right)$ 的下界,通过它,真正的 FMI 在一定程度上最大化。
3.2 Topology-Aware Mutual Information
受 Theorem 1 分解的启发,我们试图从图的另一个方面(即拓扑视图)构造可训练的权值,从而使 $w_{ij}$ 的值更灵活,并捕获图的固有属性
Definition 2 (Graphical mutuak mutual information). The MI between the hidden vector $\boldsymbol{h}_{i}$ and its support graph $\mathcal{G}_{i}=\left(\boldsymbol{X}_{i}, \boldsymbol{A}_{i}\right)$ is defined as
$\begin{array}{c} I\left(\boldsymbol{h}_{i} ; \mathcal{G}_{i}\right):=\sum\limits _{j}^{i_{n}} w_{i j} I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)+I\left(w_{i j} ; \boldsymbol{a}_{i j}\right), \\ \text { with } w_{i j}=\sigma\left(\boldsymbol{h}_{i}^{\mathrm{T}} \boldsymbol{h}_{j}\right) \end{array}$
其中 $\boldsymbol{x}_{j}$ 和 $i_{n}$ 的定义与 Theorem 1 相同,$\boldsymbol{a}_{i j}$ 是邻接矩阵 $A$ 中的边权值,$\sigma(\cdot)$ 是一个 $ \text{sigmoid}$ 函数
$Eq.10$ 中第一项的 $w_{i j}$ 衡量了一个局部 $\text{MI}$ 对全局 $\text{MI}$ 的贡献,通过 $\boldsymbol{h}_{i}$ 和 $\boldsymbol{h}_{j}$ 之间的相似性来实现 $I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)$ 贡献 (即 $w_{i j}= \sigma\left(\boldsymbol{h}_{i}^{T} \boldsymbol{h}_{j}\right)$ ) 。同时,$I\left(w_{i j} ; \boldsymbol{a}_{i j}\right. )$ 最大化 $w_{i j} $ 和输入图的边权重 $\boldsymbol{a}_{i j}$ 之间的 $\text{MI}$ ,以强制 $w_{i j} $ 符合拓扑关系。
从这个意义上讲,贡献的程度将与拓扑结构中的接近度一致,这通常被认为是,如果节点 $j$“更接近”节点 $i$,$w_{i j}$ 可能更大,否则 $w_{i j}$ 可能更小。该策略弥补了 FMI 只关注节点特征的缺陷,并使局部 $\text{MI}$ 自适应地对全局 $\text{MI}$ 有贡献。
请注意,$Eq.10$ 适用于一般情况。对于某些特定的情况下,我们可以稍微修改以提高效率。例如,当处理未加权图时,我们可以用负交叉熵损失替换第二个$\text{MI}$ 项 $I\left(w_{i j} ; \boldsymbol{\alpha}_{i j}\right)$。最小化交叉熵也有助于 $\text{MI}$ 最大化,并提供了一个更有效的计算。
$Eq.10$ 有几点好处。首先,这种 $\text{MI}$ 对输入图的同构变换是不变的。其次,它在计算上是可行的,因为右边的每个分量都可以用 MINE 来估计。更重要的是,GMI 在捕获原始输入信息方面比DGI更强大,因为它在细粒度节点级别的隐藏向量和节点和边缘的输入特征方面具有显式的相关性。
3.3 Maximization of GMI
借助于 MINE ,我们最大化 Eq.10 的第二项。在 MINE 中使用联合分布和边缘乘积之间的 KL 散度的 Donsker Varadhan(DV) 表示来估计 $\text{MI}$ 的下界。
由于更关注的是最大化 $\text{MI}$,而不是获得其特定值,所以可以使用其他非 KL 散度的替代方案,如 Jensen-Shannon MI estimator (JSD) 和 Noise-Contrastive estimator (infoNCE) 来代替它。
本文为了有效性和效率,选用 JSD 估计器,因为 infoNCE 估计器对负面采样策略(负面样本的数量)敏感,因此可能成为固定可用内存的大规模数据集的瓶颈。相反,JSD 估计器对负抽样策略的不敏感性及其在许多任务上的良好性能使其更适合我们的任务。
接着作者通过下式计算 Eq.10 中的第一项:
$I\left(\boldsymbol{h}_{i} ; \boldsymbol{x}_{j}\right)=-s p\left(-\mathcal{D}_{w}\left(\boldsymbol{h}_{i}, \boldsymbol{x}_{j}\right)\right)-\mathbb{E}_{\tilde{\mathbb{P}}}\left[\operatorname{sp}\left(\mathcal{D}_{w}\left(\boldsymbol{h}_{i}, \boldsymbol{x}_{j}^{\prime}\right)\right)\right]\quad\quad\quad(11)$
其中
-
- $\mathcal{D}_{w}: D \times D^{\prime} \rightarrow \mathbb{R}$ 是由参数为 $w$ 的神经网络构建的判别器;
- $x^{\prime}{ }_{j}$ 是来自 $\tilde{\mathbb{P}}=\mathbb{P}$ 的负样本;
- $s p(x)=\log \left(1+e^{x}\right)$,即soft-plus function;
正如 3.2 节中提到的,我们通过计算交叉熵而不是使用 JSD 估计器使 $I\left(w_{i j} ; \boldsymbol{\alpha}_{i j}\right)$ 最大化,因为我们在实验中处理的图是未加权的。
$I\left(w_{i j} ; \boldsymbol{a}_{i j}\right)=\boldsymbol{a}_{i j} \log w_{i j}+\left(1-\boldsymbol{a}_{i j}\right) \log \left(1-w_{i j}\right)\quad\quad\quad(12)$
通过最大化所有隐藏向量 $H$ 上的 Eq.11 和 Eq.12 ,得到了 GMI 优化的完整目标函数$I\left(\boldsymbol{h}_{i} ; \mathcal{G}_{i}\right)$ 。此外,我们还可以进一步添加权衡参数来平衡 Eq.11 和 Eq.12 的灵活性。
4 Experiments
在本节中,通过评估 GMI 在两个常见任务上的性能:节点分类(transductive and inductive)和链路预测。GMI 和另外两种无监督算法( EP-B 和 DGI )之间的另一个相对公平的比较进一步证明了其有效性。我们还提供了 t-SNE 图的可视化,并分析了模型深度的影响。
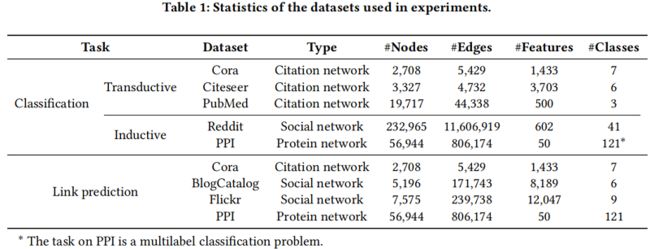
4.1 Datasets
4.2 Classification
4.3 Effectiveness of Objective Function
4.4 Link Prediction
4.5 Visualization
论文参考类型
1~最大化神经网络输入与输出的互信息
InfoMax [3]
ICA [1, 21]
2~解决 1 无法计算高维连续变量之间的互信息
Mutual Information Neural Estimation (MINE) [2] 及其涉及到的 JS 散度 [30]
3~基于随机游走和分解的传统方法
[6, 15, 33, 34, 39]
4~图上监督表示学习方法
[7, 9, 25, 40, 48]
5~图上无监督表示学习方法
[11, 16, 41]
GraphSAGE [16]
DGI [41] :无法保存输入图的精细信息。