Transformer和自注意力机制Self-Attention详解和时间复杂度计算+Image Transformer简介
Transformer
背景
注意力机制已经在编码器解码器模型中广泛应用,极大提升了模型性能。我们为什么不能尝试完全抛开RNN、CNN等传统结构,直接尝试使用注意力机制来捕捉输入和输出之间的依赖呢?
结构
输入序列是 ( x 1 , . . . , x n ) (x_1, ..., x_n) (x1,...,xn),编码器将其映射到向量表示 ( z 1 , . . . , z n ) (z_1, ..., z_n) (z1,...,zn),解码器再根据此中间向量产生序列 ( y 1 , . . . , y m ) (y_1, ..., y_m) (y1,...,ym)。解码器在每一时间步都会读取之前输出的元素并产生序列中一个新元素。

编码器由 N = 6 N=6 N=6个一模一样的单元组成。每个单元包含两个子单元。第一个是多头自注意力机制(multi-head self-attention mechanism),第二个是全连接的前馈网络,激活函数是ReLU。这两个子单元都是用了残差连接(residual connection)和层归一化(layer normalization)。所以每一个子单元的输出都是 L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm(x + Sublayer(x)) LayerNorm(x+Sublayer(x))。为了使模型能够正常拼接,所有层都使用相同的维度 d = 512 d =512 d=512。自注意力层的查询、键、值都来自前一层编码器的输出。编码器中的每个位置都可以注意到编码器上一层中的所有位置。
解码器与编码器几乎一样,只不过在中间多增加了一层多头注意力机制(encoder-decoder attention)来处理编码器的输出。该注意力机制的查询来自于解码器的上一层,键值对来自于解码器的输出。编码器中的每个位置都可以注意到输入中的所有位置。模拟了seq2seq模型中的注意力机制。
同时,第一个单元即多头自注意力机制为了确保解码器不会读取当前位置之后的信息进行了遮挡(masking)操作,将对应位置的值填充为 − ∞ -\infty −∞。
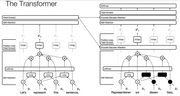
在模型中,在两个Embedding层之间共享相同的权重矩阵和pre-softmax线性变换。在Embedding层,权重被乘以了 d m o d e l \sqrt{d_{model}} dmodel。
补充:
层归一化与批归一化(batch normalization)的区别。两者思路相近,只是归一化的对象不同。批归一化会对一个小批的输入在相同神经元上的值进行归一化,即对一批数据中每一个特征进行归一化。层归一化是对同一输入在该层不同神经元上的值进行归一化,与批没有关系,即对于每个样本做归一化。
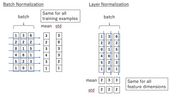
如果使用 i i i代表样本,使用 j j j代表特征。共有 m m m个样本, n n n个特征。
BatchNorm
μ j = 1 m ∑ i = 1 m x i j σ j 2 = 1 m ∑ i = 1 m ( x i j − μ j ) 2 x ^ i j = x i j − μ j σ j 2 + ϵ \mu_j = \frac 1 m \sum_{i=1}^m x_{ij} \\\\ \sigma_j^2 = \frac 1 m \sum_{i=1}^m (x_{ij} - \mu_j)^2\\\\ \hat x_{ij} = \frac {x_{ij} - \mu_j} {\sqrt{\sigma_j^2 + \epsilon}} μj=m1i=1∑mxijσj2=m1i=1∑m(xij−μj)2x^ij=σj2+ϵxij−μj
LayerNorm
μ i = 1 n ∑ j = 1 n x i j σ i 2 = 1 n ∑ j = 1 n ( x i j − μ j ) 2 x ^ i j = x i j − μ j σ i 2 + ϵ \mu_i = \frac 1 n \sum_{j=1}^n x_{ij} \\\\ \sigma_i^2 = \frac 1 n \sum_{j=1}^n (x_{ij} - \mu_j)^2\\\\ \hat x_{ij} = \frac {x_{ij} - \mu_j} {\sqrt{\sigma_i^2 + \epsilon}} μi=n1j=1∑nxijσi2=n1j=1∑n(xij−μj)2x^ij=σi2+ϵxij−μj
注意力
注意力函数可以被看成是将查询(query)和键值对(key-value pair)的集合映射到输出的操作。其中,查询、键、值、输出都是向量。输出是值的加权和,权重是根据查询和键使用兼容性函数(compatibility function)来进行计算的。
缩放点积注意力
缩放点积注意力(Scaled Dot-Product Attention)的输入包括查询、键、值。前两者的维度是 d k d_k dk,值的维度是 d v d_v dv。首先,计算查询和所有键的点积,分别除以维度的平方根,再运用softmax函数得到权重。

在实操中,我们会同时计算一批查询,而非一个个计算。
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V Attention(Q,K,V)=softmax(dkQKT)V
两个常用的注意力函数是加法注意力和乘法注意力(点积)。后者会更快一些,且更节省空间。所以这里使用的是后者。当 d k d_k dk非常大,且不考虑使用 d k d_k dk平方根进行缩放的情况下,加法注意力的性能远优于乘法注意力。可能的原因是乘法注意力经过softmax函数处理之后,进入到了某些梯度非常小的区域,难以优化。所以,此处进行了缩放。
多头注意力
将查询、键、值使用不同的经过学习的参数线性投影到 d k 、 d k 、 d v d_k、d_k、d_v dk、dk、dv维度上 h h h次,有很好的效果。在每一次投影中,都会产生一个 d v d_v dv维度的输出。将这些输出拼接,再进行一次投影,可以得到最终输出。

多头注意力帮助模型共同关注来自不同位置的不同表示子空间的信息。
M u l t i H e a d ( Q , K , V ) = C o n c a t ( h e a d 1 , . . . , h e a d h ) W O h e a d i = A t t e n t i o n ( Q W i Q , K W i K , V W i V ) MultiHead(Q,K,V) = Concat(head_1,...,head_h) W^O \\\\ head_i = Attention(QW_i^Q, KW_i^K, VW_i^V) MultiHead(Q,K,V)=Concat(head1,...,headh)WOheadi=Attention(QWiQ,KWiK,VWiV)
参数的维度如下。 W i Q ∈ R d m o d e l ∗ d k W_i^Q \in R^{d_{model}*d_k} WiQ∈Rdmodel∗dk, W i K ∈ R d m o d e l ∗ d k W_i^K \in R^{d_{model}*d_k} WiK∈Rdmodel∗dk, W i V ∈ R d m o d e l ∗ d v W_i^V \in R^{d_{model}*d_v} WiV∈Rdmodel∗dv, W i O ∈ R h d v ∗ d m o d e l W_i^O \in R^{hd_v*d_{model}} WiO∈Rhdv∗dmodel。
模型中超参数 h = 8 h = 8 h=8, d k = d v = d m o d e l / h = 64 d_k = d_v = d_{model}/h = 64 dk=dv=dmodel/h=64。模型将隐藏层的大小,即 d d d进行了拆分。
h i d d e n _ s i z e ( d ) = n u m _ a t t e n t i o n _ h e a d s ( m ) ∗ a t t e n t i o n _ h e a d _ s i z e ( a ) hidden\_size(d) = num\_attention\_heads(m)*attention\_head\_size(a) hidden_size(d)=num_attention_heads(m)∗attention_head_size(a)
并且改造了数组维数(reshape),所以Q和K的维度都是(m,n,a)。多头注意力每个头的维度相对而言都降低了,所以消耗的算力与满维度的单头注意力相似。
自注意力的核心是用文本中的其它词来增强目标词的语义表示,从而更好的利用上下文的信息。对于自注意力机制,一般会说它的 q=k=v,这里的相等实际上是指它们来自同一个基础向量,而在实际计算时,它们是不一样的,因为这三者都是乘了参数矩阵的。如果不乘,每个词对应的q、k、v就是完全一样的。在相同量级的情况下, q i q_i qi与 k i k_i ki点积的值会是最大的。在softmax后的加权中,该词本身所占的比重将会是最大的,使得其他词的比重很少,无法有效利用上下文信息来增强当前词的语义表示。
位置编码
模型中不包含循环和卷积,位置编码(positional encoding)可以让模型学到相对或绝对的位置信息。维度也是 d m o d e l d_{model} dmodel。位置编码的选择是多种多样的,可以是经过学习的,也可以是固定的。
在Attention Is All You Need论文中使用了正弦余弦函数。
P E ( p o s , 2 i ) = s i n ( p o s / 1000 0 2 i / d m o d e l ) P E ( p o s , 2 i + 1 ) = c o s ( p o s / 1000 0 2 i / d m o d e l ) PE(pos, 2i) = sin(pos/10000^{2i/d_{model}}) \\\\ PE(pos, 2i+1) = cos(pos/10000^{2i/d_{model}}) PE(pos,2i)=sin(pos/100002i/dmodel)PE(pos,2i+1)=cos(pos/100002i/dmodel)
位置用 p o s pos pos表示,而 i i i代表维度 i i i。也就是说,位置编码的每个维度对应一个正弦信号。波长形成了从 2 π 2\pi 2π到 10000 ⋅ 2 π 10000·2π 10000⋅2π的几何级数。这个函数鲤鱼模型学习相对位置信息。
衡量标准
我们从三方面衡量模型的优劣。第一是性能,指标是时间复杂度。第二是可并行性,指标是所需的最小顺序操作数。第三是处理长依赖的能力,指标是网络中远程依赖项之间的路径长度。最后一个是长序列处理任务的关键,我们希望路径越短越好。
先规定一下参数表示。我们用 n n n表示序列长度,用 d d d表示每个词的向量维度,用 k k k表示卷积核的大小,用 r r r表示限制版自注意力中临域的大小。
| Layer Type | Complexity | Sequential Operations | Max Path Length |
|---|---|---|---|
| Self-Attention | O ( n 2 d ) O(n^2d) O(n2d) | O ( 1 ) O(1) O(1) | O ( 1 ) O(1) O(1) |
| Recurrent | O ( n d 2 ) O(nd^2) O(nd2) | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) |
| Convolutional | O ( k n d 2 ) O(knd^2) O(knd2) | O ( 1 ) O(1) O(1) | O ( l o g k ( n ) ) O(log_k(n)) O(logk(n)) |
| Self-Attention (restricted) | O ( r n d ) O(rnd) O(rnd) | O ( 1 ) O(1) O(1) | O ( n / r ) O(n/r) O(n/r) |
自注意力包括三个步骤:相似度计算、softmax和加权求和。相似度计算的时间复杂度是 O ( n 2 d ) O(n^2d) O(n2d),因为可以看成(n,d)和(d,n)两个矩阵的相乘。softmax的时间复杂度是 O ( n 2 ) O(n^2) O(n2)。加权求和的时间复杂度是 O ( n 2 d ) O(n^2d) O(n2d),同样可以看成(n,n)和(n,d)的矩阵相乘。
我们发现,从性能角度说,该模型在序列长度过长时表现不如RNN,不过在可并行性和处理长依赖的能力上具有绝对的优势。我们的任务,就是想办法尽可能用词向量维度来弥补长度的劣势,只要 d < n d < n d<n,那么模型的性能也是杠杠的。
效果
在两个机器翻译任务上的实验表明,模型具有更高的质量,同时具有更强的并行性和更少的训练时间。模型在WMT 2014英德翻译任务中达到28.4 BLEU,比现有的最佳结果(包括集成)提高了2 BLEU。在WMT 2014英法翻译任务中,模型在8个gpu上训练3.5天后,建立的单模型最先进的BLEU分数为41.8,这只是文献中最好模型训练成本的一小部分。通过成功地将其应用于具有大量和有限训练数据的英语选区解析,该转换器可以很好地推广到其他任务。
局部自注意力
上面介绍的原始版自注意力,每一个点都会注意到输入中的所有点。当 n n n过大时,这是不现实的。当Niki Parmar和Ashish Vaswani试图使用Transformer处理图像的时候,就遇到了这个问题。输出的图片是32*32,有3个通道,一共3072个像素点。
解决的办法就是限制自注意力的范围,使用局部自注意力(local self-attention)。基本思想就和卷积网络一样,通过移动卷积核取特征。局部自注意力的区域有两种取法,1D和2D。

在1D中,长度是 l q l_q lq,如果需要可以padding。对于每个不重叠的查询块 Q Q Q,和额外 l m l_m lm个之前产生的相应的像素,构造记忆块 M M M。记忆块的位置和查询块相同。产生的记忆块是连续的。
在2D中,生成了从左到右和从上到下用灰色线勾画的块。我们使用大小为 l q l_q lq(由高度和宽度 l q = w q ⋅ h q l_q = w_q·h_q lq=wq⋅hq指定)的二维查询块,以及内存块分别以 h m h_m hm、 w m w_m wm和 w m w_m wm像素扩展查询块的顶部、左边和右边。
2D局部注意力平衡水平和垂直条件更均匀。使用1D,容易导致在给定位置旁边的像素越来越多地占主导地位,而忽视其上面的像素。
损失函数
使用最大似然。
l o g p ( x ) = ∑ t = 1 h w 3 l o g p ( x t ∣ x < t ) log p(x) = \sum_{t=1}^{hw3} log\ p(x_t | x_{
分类分布(categorical distribution)捕获每个强度值作为离散结果,并跨渠道分解。每个像素有 256 ∗ 3 = 768 256*3 = 768 256∗3=768个参数。不同于分类分布,离散混合逻辑回归(discretized mixture of logistics, DMOL)能额外捕捉两个重要属性:像素强度的顺序性质和通道间的依赖。而且参数所需要的个数少得多。
效果

两个任务。第一个是图像还原。第二个是图像补充。每组第一张图片是输入,第二张图片是模型输出,第三张是原图。可以看出效果还挺不错的。
Reference
- Natural Language Processing with Deep Learning, Stanford University, CS224N, 2019 winter
- Attention Is All You Need, Ashish Vaswani et al.
- Image Transformer, Niki Parmar et al.
- 超细节的 BERT/Transformer 知识点,海晨威
- Transformer图解,李理