强化学习进阶——DQN

目录

预备知识

基本概念

目标和约束条件

MDP马尔可夫决策过程

假设

基本概念

计算价值函数

Action-Value Function动作价值函数

Optimal value function最优价值函数

策略迭代和值迭代

Q-Learning

Q-Learning算法

EE问题

DQN

Q-Learning神经网络化

DQN算法及其改进

NIPS DQN

Natural DQN

Double DQN

Prioritised replay

Dueling Network

---

在强化学习基础——bandit中，我们已经登堂入室，初窥强化学习的门径。不断探索的我们，怎么可能停滞不前呢？所以接下来，我会我们将重点介绍强化学习进阶——DQN。

预备知识

基本概念

在人工智能领域，一般用智能体Agent来表示一个具备行为能力的物体，比如机器人，无人车，人等等。那么增强学习考虑的问题就是智能体Agent和环境Environment之间交互的任务。

不管是什么样的任务，都包含了一系列的动作Action,观察Observation还有反馈值Reward。所谓的Reward就是Agent执行了动作与环境进行交互后，环境会发生变化，变化的好与坏就用Reward来表示。

agent、environment、state、action、reward共同构建了强化学习，如下图：

目标和约束条件

强化学习目标是获取尽可能多的reward，如何量化reward？

Agent都是根据当前的观察来确定下一步的动作。观察Observation的集合就作为Agent的所处的状态state。状态state和动作action之间存在映射关系，即一个状态对应不同的动作的概率。

状态state到动作action过程，称为策略policy，表示为。

因此，增强学习的任务就是找到一个最优的策略Policy从而使Reward最多。

一开始并不知道最优的策略是什么，因此往往从随机的策略开始，使用随机的策略进行试验，就可以得到一系列的状态,动作和反馈：

这就是一系列的样本sample，增强学习需要这些样本改进policy。

MDP马尔可夫决策过程

假设

马尔可夫决策过程（MDP，Markov Decision Process）基本假设如下：

• 未来只取决于当前，即下一步的状态只取决于当前的状态，与过去的状态没有关系；
• 上帝不摘骰子，如果输入是确定的，那么输出也一定是确定的；

基本概念

一个基本MDP可以用（S,A,P）表示，S表示状态，A表示动作，P表示状态转移概率。状态对应动作的概率，有了动作，下一个状态也是确定的。

那么怎么描述状态的好坏？引入回报Return来表示某个时刻t的状态将具备的回报：

上面R是Reward反馈，λ是discount factor折扣因子，一般小于1，就是说一般当下的反馈是比较重要的，时间越久，影响越小。

实际上除非整个过程结束，否则显然我们无法获取所有的reward来计算出每个状态的Return，因此引入价值函数（Value Function)来表示未来潜在的价值：

计算价值函数

基于反复试验value Function评估，数学公式如下：

Bellman公式表明，value function是可以通过迭代计算出来的。

Action-Value Function动作价值函数

考虑到每个状态之后都有多种动作可以选择，每个动作之下的状态又多不一样，我们更关心在某个状态下的不同动作的价值。显然。如果知道了每个动作的价值，那么就可以选择价值最大的一个动作去执行了。动作价值函数表示为：

Optimal value function最优价值函数

计算动作价值函数是不够的，需要的是最有策略，求解最有策略方法有value-based，policy-based和model-based方法。

最优价值策略函数和一般动作价值函数关系：

最优价值策略函数是所有策略的价值函数的最大值。

策略迭代和值迭代

策略迭代

Policy Iteration是直接使用Bellman方程，其目的是通过迭代计算value function 价值函数的方式来使policy收敛到最优。其基本步骤如下：

• Policy Evaluation 策略评估。目的是 更新Value Function，或者说更好的估计基于当前策略的价值；
• Policy Improvement 策略改进。 使用 greedy policy 产生新的样本用于第一步的策略评估；

本质上就是使用当前策略产生新的样本，然后使用新的样本更好的估计策略的价值，然后利用策略的价值更新策略，然后不断反复。理论可以证明最终策略将收敛到最优。

值迭代

Value Iteration是使用Bellman 最优方程得到，和Policy Iteration有什么区别：

policy iteration使用bellman方程来更新value，最后收敛的value 即是当前policy下的value值（所以叫做对policy进行评估），目的是为了后面的policy improvement得到新的policy。

而value iteration是使用bellman 最优方程来更新value，最后收敛得到的value即就是当前state状态下的最优的value值。因此，只要最后收敛，那么最优的policy也就得到的。因此这个方法是基于更新value的，所以叫value iteration。

value iteration比policy iteration更直接，不过理想条件下需要遍历所有的状态，这在复杂一些的问题上就基本不可能了。

Q-Learning

介绍以上强化学习储备知识后，下面开始进入正题了。首先从Q-Learning开始。

Q-Learning算法

Q Learning是基于value iteration得到。但value iteration每次都对所有的Q值更新一遍，也就是所有的状态S和动作A。一个s一个a对应一个Q值，需要维护一张S*A的Q值表，如下：

			...
	Q(1,1)	Q(1,2)		Q(1,m)
	Q(2,1)	Q(2,2)		Q(2,m)
...
	Q(n,1)	Q(n,2)		Q(n,m)

因此只能使用有限的样本进行操作。为此Q Learning提出了一种更新Q值的办法：

这里并没有直接将这个Q值（是估计值）直接赋予新的Q，而是采用渐进的方式类似梯度下降，朝target迈近一小步，取决于α,这就能够减少估计误差造成的影响。类似随机梯度下降，最后可以收敛到最优的Q值。其算法流程如下：

EE问题

Q-Learning完全不考虑model模型也就是环境的具体情况，只考虑看到的环境及reward，因此是model-free的方法。那么怎样选择policy来生成action呢？有两种做法：

• 探索阶段：随机生成动作；
• 利用阶段：根据当前的Q值计算出一个最优的动作，这个policy π称之为greedy policy贪婪策略;

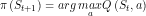使用随机的动作就是exploration，有利于更新Q值，获得更好的policy。而使用greedy policy则是exploitation，利用policy，可以得到更好的测试效果用于判断算法是否有效。

将两者结合起来就是所谓的策略，一般是一个很小的值，决定exploration和exploitation的比例。

DQN

Q-Learning神经网络化

当状态和动作空间是高维连续时，使用Q-Table不现实。如何解决维度灾难问题呢？答案是价值函数近似(Value Function Approximation)。其本质就是用一个函数近似Q值的分布，即：

DQN不用Q表记录Q值，而是用神经网络来预测Q值，并通过不断更新神经网络从而学习到最优的行动路径。

而Q值神经网络化要有海量带有标签的样本，如何实现呢？

利用Q-Learning中Reward和Q计算出来的目标Q值:

把目标Q值作为标签，让Q值趋近于目标Q值。

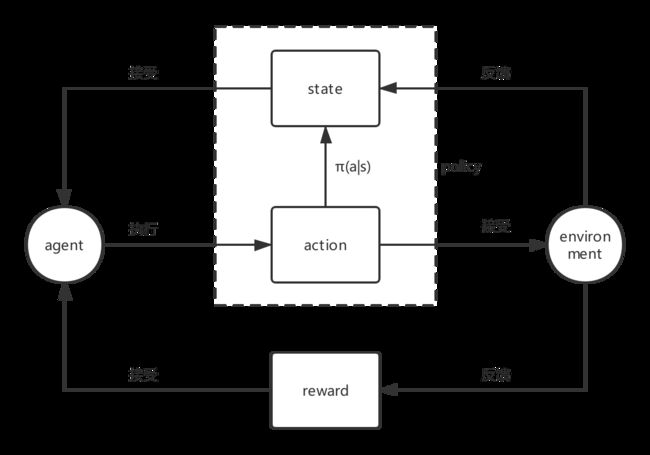
因此，Q网络训练的损失函数就是：

DQN算法及其改进

NIPS DQN

第一个版本的DQN(NIPS 2013提出的)，在基本的Deep Q-Learning算法的基础上使用了Experience Replay经验池，算法流程如下：

主要涉及存储样本和采样问题，考虑到样本之间具有连续性，如果每次得到样本就更新Q值，受样本分布影响，效果会不好。因此，把样本先存起来，然后随机采样，降低数据相关性，这就是Experience Replay的意思。按照脑科学的观点，人的大脑也具有这样的机制，就是在回忆中学习。

Natural DQN

Nature DQN是在NPIS DQN上增加Target Q网络。也就是我们在计算目标Q值时使用专门的一个目标Q网络来计算，而不是直接使用预更新的Q网络。这样做的目的是为了减少目标计算与当前值的相关性。

如上公式，计算目标Q值的网络使用的参数是w-，而不是w。Target Q仍从Q网络中来，只不过是延迟更新。也就是每次等训练了一段时间再将当前Q网络的参数值复制给目标Q网络。

Double DQN

目的是减少max Q值计算带来的计算偏差，或者称为过度估计（over estimation）问题，用当前的Q网络w来选择动作，用目标Q网络来计算目标Q。其改进公式如下：

部分伪代码如下：

# 定义双网络结构
def build_layers(s,c_name,n_l1,w_initializer,b_initializer):
    with tf.variable_scope('l1'):
        w1 = tf.get_variable(name='w1',shape=[self.n_features,n_l1],initializer=w_initializer,collections=c_name)
        b1 = tf.get_variable(name='b1',shape=[1,n_l1],initializer=b_initializer,collections=c_name)
        l1 = tf.nn.relu(tf.matmul(s,w1)+b1)
    with tf.variable_scope('l2'):
        w2 = tf.get_variable(name='w2',shape=[n_l1,self.n_actions],initializer=w_initializer,collections=c_name)
        b2 = tf.get_variable(name='b2',shape=[1,self.n_actions],initializer=b_initializer,collections=c_name)
        out = tf.matmul(l1,w2) + b2
    return out


# ------------------ build evaluate_net ------------------
with tf.variable_scope('eval_net'):
    c_names = ['eval_net_params',tf.GraphKeys.GLOBAL_VARIABLES]
    n_l1 = 20
    w_initializer = tf.random_normal_initializer(0,0.3)
    b_initializer =tf.constant_initializer(0.1)
    self.q_eval = build_layers(self.s,c_names,n_l1,w_initializer,b_initializer)

# ------------------ build target_net ------------------
with tf.variable_scope('target_net'):
    c_names = ['target_net_params', tf.GraphKeys.GLOBAL_VARIABLES]

    self.q_next = build_layers(self.s_, c_names, n_l1, w_initializer, b_initializer)

Prioritised replay

不同样本的重要性是不一样的，优化记忆库抽取。其改进数学公式如下：

按误差的大小进行重要程度排序，误差越大说明越需要被学习。但是为了效率，不能每次都排一遍太麻烦，所以使用sumtree(线段树)排序相对来说就简单了。

SumTree 是一种树形结构, 每片树叶存储每个样本的优先级 p, 每个树枝节点只有两个分叉, 节点的值是两个分叉的合, 所以 SumTree 的顶端就是所有p的和，如下：

抽样时, 我们会将 p 的总合 除以 batch size, 分成 batch size 那么多区间, (n=sum(p)/batch_size). 如果将所有 node 的 priority 加起来是42的话, 我们如果抽6个样本, 这时的区间拥有的 priority 可能是这样：

[0-7], [7-14], [14-21], [21-28], [28-35], [35-42]

部分伪代码如下：

# ISWeight计算
def sample(self, n):
        b_idx, b_memory, ISWeights = np.empty((n,), dtype=np.int32), np.empty((n, self.tree.data[0].size)), np.empty((n, 1))
        pri_seg = self.tree.total_p / n       # priority segment
        self.beta = np.min([1., self.beta + self.beta_increment_per_sampling])  # max = 1

        min_prob = np.min(self.tree.tree[-self.tree.capacity:]) / self.tree.total_p     # for later calculate ISweight
        if min_prob == 0:
            min_prob = 0.00001
        for i in range(n):
            a, b = pri_seg * i, pri_seg * (i + 1)
            v = np.random.uniform(a, b)
            idx, p, data = self.tree.get_leaf(v)
            prob = p / self.tree.total_p
            ISWeights[i, 0] = np.power(prob/min_prob, -self.beta)
            b_idx[i], b_memory[i, :] = idx, data
        return b_idx, b_memory, ISWeights


# 采样节点
def get_leaf(self, v):
        """
        Tree structure and array storage:
        Tree index:
             0         -> storing priority sum
            / \
          1     2
         / \   / \
        3   4 5   6    -> storing priority for transitions
        Array type for storing:
        [0,1,2,3,4,5,6]
        """
        parent_idx = 0
        while True:     # the while loop is faster than the method in the reference code
            cl_idx = 2 * parent_idx + 1         # this leaf's left and right kids
            cr_idx = cl_idx + 1
            if cl_idx >= len(self.tree):        # reach bottom, end search
                leaf_idx = parent_idx
                break
            else:       # downward search, always search for a higher priority node
                if v <= self.tree[cl_idx]:
                    parent_idx = cl_idx
                else:
                    v -= self.tree[cl_idx]
                    parent_idx = cr_idx

        data_idx = leaf_idx - self.capacity + 1
        return leaf_idx, self.tree[leaf_idx], self.data[data_idx]


# 更新sumTree权重
def batch_update(self, tree_idx, abs_errors):
        abs_errors += self.epsilon  # convert to abs and avoid 0
        clipped_errors = np.minimum(abs_errors, self.abs_err_upper)
        ps = np.power(clipped_errors, self.alpha)
        for ti, p in zip(tree_idx, ps):
            self.tree.update(ti, p)

def update(self, tree_idx, p):
        change = p - self.tree[tree_idx]
        self.tree[tree_idx] = p
        # then propagate the change through tree
        while tree_idx != 0:    # this method is faster than the recursive loop in the reference code
            tree_idx = (tree_idx - 1) // 2
            self.tree[tree_idx] += change

Dueling Network

考虑到有些state可能无论做什么动作，对下一个state都没有多大的影响。

Dueling DQN考虑将Q网络分成两部分，第一部分是仅仅与状态S有关，与具体要采用的动作A无关，这部分我们叫做价值函数部分，记做V(S,w,α),第二部分同时与状态状态S和动作A有关，这部分叫做优势函数(Advantage Function)部分，记为A(S,A,w,β)，那么最终我们的价值函数可以重新表示为：

Q(S,A,w,α,β)=V(S,w,α)+A(S,A,w,β)

其中，w是公共部分的网络参数，而α是价值函数独有部分的网络参数，而β是优势函数独有部分的网络参数。

其部分伪代码如下：

def create_Q_network(self):
    # input layer
    self.state_input = tf.placeholder("float", [None, self.state_dim])
    # network weights
    with tf.variable_scope('current_net'):
        W1 = self.weight_variable([self.state_dim,20])
        b1 = self.bias_variable([20])

        # hidden layer 1
        h_layer_1 = tf.nn.relu(tf.matmul(self.state_input,W1) + b1)

        # hidden layer  for state value
        with tf.variable_scope('Value'):
          W21= self.weight_variable([20,1])
          b21 = self.bias_variable([1])
          self.V = tf.matmul(h_layer_1, W21) + b21

        # hidden layer  for action value
        with tf.variable_scope('Advantage'):
          W22 = self.weight_variable([20,self.action_dim])
          b22 = self.bias_variable([self.action_dim])
          self.A = tf.matmul(h_layer_1, W22) + b22

          # Q Value layer
          self.Q_value = self.V + (self.A - tf.reduce_mean(self.A, axis=1, keep_dims=True))

    with tf.variable_scope('target_net'):
        W1t = self.weight_variable([self.state_dim,20])
        b1t = self.bias_variable([20])

        # hidden layer 1
        h_layer_1t = tf.nn.relu(tf.matmul(self.state_input,W1t) + b1t)

        # hidden layer  for state value
        with tf.variable_scope('Value'):
          W2v = self.weight_variable([20,1])
          b2v = self.bias_variable([1])
          self.VT = tf.matmul(h_layer_1t, W2v) + b2v

        # hidden layer  for action value
        with tf.variable_scope('Advantage'):
          W2a = self.weight_variable([20,self.action_dim])
          b2a = self.bias_variable([self.action_dim])
          self.AT = tf.matmul(h_layer_1t, W2a) + b2a

          # Q Value layer
          self.target_Q_value = self.VT + (self.AT - tf.reduce_mean(self.AT, axis=1, keep_dims=True))