植物大战栈的实现+顺序表和链表的对比——纯C

“不以物喜，不以己悲”

猛戳订阅 纯C详解数据结构专栏

顺序表和链表的对比

顺序表与链表时间复杂度比较

名称	访问	查找	插入	删除
顺序表	O(1)	O(n)	O(n)	O(n)
链表	O(n)	O(n)	O(1)	O(1)
有序数组	O(1)	O(logN)	O(n)	O(n)
有序链表	O(n)	O(n)	O(1)	O(1)

这里的链表指的链表中的扛把子：带头双向循环链表。
顺序表和链表其实是相辅相成的结构，各有各的适用场景。

	顺序表	链表
优点	物理空间是连续的，方便用下标随机访问，适合排序和二分查找	按需申请或释放空间，不浪费空间。
优点	尾插，尾删效率高。CPU高速缓存命中率高	任意位置可以插入删除效率高O(1)
缺点	由于需要物理空间连续，空间需要扩容，扩容本身有消耗。其次扩容机制还存在一定的空间的浪费，因为每次以二倍扩。扩的倍数少了，又会导致连续扩。整体来说问题不大，可以空间换时间。	不支持下标的随机访问。有些算法不适合在他上面进行，如:二分查找和排序等。
缺点	头部或者中部插入删除，需要挪动数据，效率低O(N)

总结：1.如果需要大量尾插，尾删，有排序需求，随机访问需求。用顺序表。2.在任意位置插入删除，或者头部，中部插入删除，用链表。

深入知识问题:面试官问：顺序表为什么CPU高速缓存命中率高？

在计算机中，三级缓存和寄存器的速度远快于内存和磁盘。

在程序编译链接后，生成可执行程序，CPU要执行这个程序，CPU去访问内存，但内存(RAM)速度太慢，CPU速度太快了，CPU嫌弃内存慢，CPU不会直接访问内存。所以这时候会先把数据加载到三级缓存(L1,L2,L3)和寄存器中。
加载原则：小数据如4或者8字节的放到寄存器中，大数据放到缓存中。CPU会看数据是否在缓存，在就叫命中，然后就直接访问。不在就叫不命中，会先把数据加载到缓存，然后在访问。所以说数据在缓存就叫命中，不在就叫不命中。

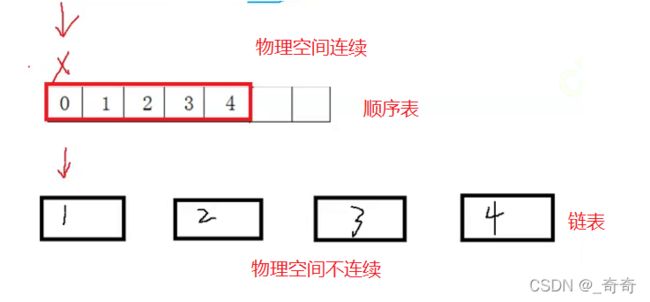
对于顺序表来说：如果不命中的话，CPU会把数据加载到内存，由于顺序表的物理空间是连续的，所以加载的时候会加载后面连续的空间。如0,1,2,3,4.所以说顺序表高速缓存命中率高。
对于链表来说：如果不命中的话，CPU会把数据加载到内存，但是链表物理空间随机的，不连续的，加载不到后面的数据。所以命中率低。

栈的实现

基本概念

栈：一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶，另一端称为栈底。栈中的数据元素遵守**后进先出LIFO（Last In First Out）**的原则。
压栈：栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。
出栈：栈的删除操作叫做出栈。出数据也在栈顶。

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小.O(1)而链表在尾上插入数据需要遍历链表时间复杂度为O(N)。
所以我们用顺序表的结构来实现栈。

创建结构体

创建了一个结构体，结构体包括一个指向顺序表的指针a，还有一个记录栈顶位置的STDataType的变量top用来访问栈顶，一个栈的最大容量capacity。

#pragma once
#include
#include
#include
#include
typedef int STDataType;

typedef struct Stack
{
	STDataType* a;//数组结构
	int top;//记录有几个值。也相当于指向最后一个值得下一个值。
	int capacity;//栈的最大容量
}ST;

初始化结构体

ps是指向结构体的指针，结构体肯定不为空，所以需要断言。

ST st;
StackInit(&st);

//初始化
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}

压栈

压栈注意top的初始值，这点是细节。top初始值为0。这点需要自己好好想想。没法用文字描述。
top是相当于指向最后一个值得下一个值。

//压栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	//满了扩容
	if (ps->top == ps->capacity)
	{
	//处理第一次栈为空的情景
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		//先把新空间给new，检查new不为空后再赋给ps->a.否则容易造成内存泄漏。
		 STDataType* new = (STDataType*)realloc(ps->a,sizeof(STDataType) * newCapacity);
		if (new == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->a = new;
		//更新栈最大容量
		ps->capacity = newCapacity;
	}
	//压栈
	ps->a[ps->top] = x;
	//更新栈顶位置
	ps->top++;
}

出栈

出栈时top必须大于0，top为0就越界了。所以必须assert

void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	--ps->top;
}

判断栈是否为空

直接返回ps->top == 0判断后的返回值就可以了。如果ps->top==0意味着栈为空则为真，返回true，否则栈不为空返回false。

//判断栈是否为空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

访问栈顶位置的值

top必须大于0，最小是1.因为栈里面不可能为空。

//访问栈顶位置的值
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->a[ps->top - 1];
}

得到栈的大小

//得到栈的大小
int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

销毁栈

拒绝内存泄漏，在程序最后一定要销毁栈。

void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;
}

如何打印

打印就是调用访问栈顶的函数，访问栈顶的值，然后再出栈，删除栈顶元素即可。这样就达到了打印的效果。

printf("%d ", StackTop(&st));
StackPop(&st);

Stack.h

#pragma once
#include
#include
#include
#include
typedef int STDataType;

typedef struct Stack
{
	STDataType* a;//数组结构
	int top;//记录栈的大小
	int capacity;//栈的最大容量
}ST;
//初始化结构体
void StackInit(ST* ps);
//压栈
void StackPush(ST* ps, STDataType x);
//出栈
void StackPop(ST* ps);
//判断栈是否为空
bool StackEmpty(ST* ps);
//访问栈顶位置的值
STDataType StackTop(ST* ps);
//得到栈的大小
int StackSize(ST* ps);
//销毁栈
void StackDestory(ST* ps);

Stack.c

#include "Stack.h"
//初始化结构体
void StackInit(ST* ps)
{
	assert(ps);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}
//销毁栈
void StackDestory(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;
}
//压栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	//满了扩容
	if (ps->top == ps->capacity)
	{
		int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
		 STDataType* new = (STDataType*)realloc(ps->a,sizeof(STDataType) * newCapacity);
		if (new == NULL)
		{
			printf("realloc fail\n");
			exit(-1);
		}
		ps->a = new;
		ps->capacity = newCapacity;
	}
	ps->a[ps->top] = x;
	ps->top++;
}
//出栈
void StackPop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	--ps->top;
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}
//访问栈顶位置的值
STDataType StackTop(ST* ps)
{
	assert(ps);
	assert(ps->top > 0);
	return ps->a[ps->top - 1];
}
//得到栈的大小
int StackSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

Test.c

#include "Stack.h"
void TestStack()
{
	ST st;
	StackInit(&st);
	StackPush(&st, 1);
	StackPush(&st, 2);
	printf("%d ", StackTop(&st));
	StackPop(&st);
	StackPush(&st, 3);
	StackPush(&st, 4);

	while (!StackEmpty(&st))
	{
		printf("%d ", StackTop(&st));
		StackPop(&st);
	}
	printf("\n");
	

	StackDestory(&st);
}
int main()
{
	TestStack();
	return 0;
}