Python日记（6）——数值积分

Python日记（6）——数值积分
每天做一个Python小练习，顺便记录一些小技巧。
在做化学实验中，一般测得的数据都是离散的，所以编写了一些程序来计算离散数据的积分。
首先，粗讲一下已知函数式的数值积分。
以下面的式子举例

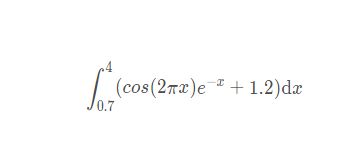
这里需要用到numpy
简单地导入以下

import numpy as np

首先，表达出要积分的函数表达式

y = np.cos(2*np.pi*x)*np.exp(-x)+1.2

原始方法
就是把函数积分化成很多且宽很小的矩形，再求所有矩形的面积总和，便可以得到积分的值。这里把x从0.7到4分解成1000分，利用linspace方法

x = np.linspace(0, 6, 1000)

然后dx作宽y作高，计算并总加所有矩形的面积

dx = x[1] - x[0]
fArea = np.sum(y*dx)
print(f'Integral area:{fArea}')

所有代码如下：

import numpy as np

x = np.linspace(0.7, 4.0, 1000)
y = np.cos(2*np.pi*x)*np.exp(-x)+1.2
dx = x[1] - x[0]
fArea = np.sum(y*dx)
print(f'Integral area:{fArea}')

结果如下：

Integral area:4.032803310221616

使用quad()函数

import math
from scipy import integrate

def func(x):
    print("x=",x)       #用于展示quad()函数对func的多次调用
    return math.cos(2*math.pi*x)*math.exp(-x)+1.2

fArea,err = integrate.quad(func,0.7,4)
print("Integral area:",fArea)

这里定义了一个函数func(),可以根据x计算y值。
​ integrate.quad()专门用于计算一元定积分，fArea,err = integrate.quad(func,0.7,4)取x值域[0.7,4]进行数值积分，在积分过程中，会反复调用func()函数计算y值。其返回一个元组，包括积分结果及误差。
​integrate.quad()计算的积分会比方法1的矩形面积求和方法更加精确。
Riemann和求积分值
可以通过把数据区间[a, b]划分成2n等份，每个小区间的长度为h=(a-b)/2n, 根据Simpson公式，可通过求和来代替积分。
（1）已知函数表达式的情况
以f = sin(x)为例，计算从0到Π的积分

import numpy as np


def simpson1(xlower, xupper, N):
    """
    Simpson公式计算积分
    :param xlower: 积分下限
    :param xupper: 积分上限
    :param N: 格点数目（对于Simpson，N必须是偶数）
    :return: None
    """
    h = (xupper-xlower)/N
    x_int = np.arange(xlower, xupper+h, h)
    res = (np.sin(xlower) - np.sin(xupper))*h/3
    for i in np.arange(1, N, 2):
        if i > len(x_int):
            break
        else:
            res += 2*h/3*(2*np.sin(x_int[i])+np.sin(x_int[i+1]))
    print(f'积分的结果为：{round(res, 12)}')


if __name__ == "__main__":
    xlower = 0
    xupper = np.pi
    N = 10
    simpson1(xlower=xlower, xupper=xupper, N=N)

输出结果为：

积分的结果为：2.000109517315

(2) 未知函数表达式的情况

import numpy as np


def simpson2(x, y, h, N):
    """
    Simpson公式计算积分
    :param x: 散点x
    :param y: 散点y
    :param h: 设置步长
    :param N: 区间部数
    :return:
    """
    res = (y[0] - y[-1])*h/3
    for i in np.arange(1, N, 2):
        if i > len(y):
            break
        else:
            res += 2*h/3*(2*y[i]+y[i+1])
    print(f'积分结果{round(res, 12)}')


if __name__ == "__main__":
    x = [0, 0.3142, 0.6283, 0.9425, 1.2566, 1.5708, 1.8805, 2.1991, 2.5133, 2.8274, 3.1416]
    y = [0, 0.3090, 0.5875, 0.8090, 0.9511, 1.0000, 0.9511, 0.8090, 0.5878, 0.3090, 0]
    h = 0.3142
    N = 10
    simpson2(x, y, h, N)

输出结果为：

积分结果为2.000301933333`