随机梯度下降法
$\theta_{t} \leftarrow \theta_{t-1}-\alpha g_{t}$
Code:
optimzer = torch.optim.SGD(model.parameters(),lr = 0.001)
权重衰减
$\theta_{t} \leftarrow(1-\beta) \theta_{t-1}-\alpha \mathbf{g}_{t}$
其中 $\mathrm{g}_{t}$ 为第 $t$ 步更新时的梯度, $\alpha$ 为学习率, $\beta$ 为权重衰减系数,一般取值比较 小,比如 0.0005。
Code:
optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,weight_decay=0.0005)
动量法
动量(Momentum)是模拟物理中的概念.一个物体的动量指的是该物体 在它运动方向上保持运动的趋势,是该物体的质量和速度的乘积.动量法(Momentum Method)是用之前积累动量来替代真正的梯度.每次迭代的梯度可以 看作加速度. 在第 $t$ 次迭代时,计算负梯度的“加权移动平均”作为参数的更新方向,
$\Delta \theta_{t}=\rho \Delta \theta_{t-1}-\alpha g_{t}=-\alpha \sum\limits_{\tau=1}^{t} \rho^{t-\tau} g_{\tau}$
Code:
optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,momentum =0.001,dampening=0.001)
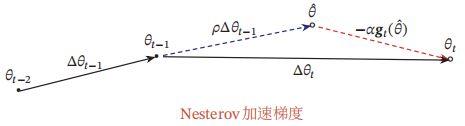
Nesterov加速梯度
Nesterov 加速梯度(Nesterov Accelerated Gradient,NAG)是一种对动量 法的改进[Nesterov, 2013; Sutskever et al., 2013],也称为Nesterov动量法(Nesterov Momentum)
在动量法中, 实际的参数更新方向 $\Delta \theta_{t}$ 为上一步的参数更新方向 $\Delta \theta_{t-1}$ 和当 前梯度的反方向 $ -g_{t}$ 的叠加. 这样, $\Delta \theta_{t}$ 可以被拆分为两步进行, 先根据 $\Delta \theta_{t-1}$ 更 新一次得到参数 $ \hat{\theta}$ , 再用 $ -g_{t}$ 进行更新.
这样,合并后的更新方向为
$\Delta \theta_{t}=\rho \Delta \theta_{t-1}-\alpha \mathfrak{g}_{t}\left(\theta_{t-1}+\rho \Delta \theta_{t-1}\right)$
其中 $\mathfrak{g}_{t}\left(\theta_{t-1}+\rho \Delta \theta_{t-1}\right)$ 表示损失函数在点 $\hat{\theta}=\theta_{t-1}+\rho \Delta \theta_{t-1}$ 上的偏导数.
Code:
optimzer = torch.optim.SGD(model.parameters(),lr = 0.001,momentum =0.001,nesterov=0.01)