关于B树和B+树以及数据库索引

MySQL优化详解请点击

了解红黑树请点击

一.B树

1.特点

对于一个m阶B树来说

• 任何节点最多m棵子树（子树数量 = 该节点关键字数量+1）
• 根节点关键字数量：1 <= n <= m-1
• 非根节点关键字数量：m/2 <= n <= m-1
• 任何一个内部节点的内部关键字是呈递增的
• 关键字两侧均有指向子树的指针，左边指针指的左子树关键字均小于该节点，右边指针关键字个数均大于该节点
• 每个关键字都和对应的数据在一块
• 外部节点不带任何信息，也不存在，代表查找失败

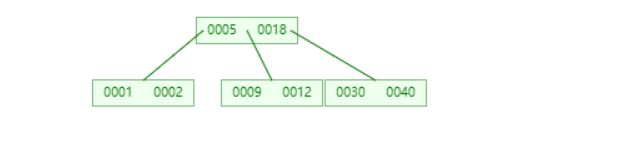
如图是一个5阶B树，可以看到，根节点的关键字个数只有22一个，根据性质，根节点有两棵子树。对于非根节点，最少有5/2=2个关键字，最多有5-1=4个关键字

2.查找

B树查找分为两个步骤

• 在B树中找节点（在磁盘进行）
• 在节点内通过顺序查找或者折半查找找关键字（在内存中进行）

一般活跃B树的根节点是常驻内存的，其余节点位于磁盘

以上图为例

• 查找22，因为是根节点，内存命中
• 查找42，根节点查找失败，42>22，一次磁盘IO将右子树[36,45]载入内存，通过比较，42位于36和45的中间节点，再一次磁盘IO将[40,42]载入内存，即可找到42
• 查找60，通过两次磁盘IO查找失败

3.插入

只需记住一句话即可：满取中向上分裂

满：一个m阶B树，每个节点最多有m-1个关键字，当大于m-1个关键字，该节点就满了

取中：就是取中间的那个关键字，奇数个关键字直接取中间，偶数个则随机取中间两个其中一个

向上分裂：以取中的那个关键字为准，关键字向上一级，两边分裂

示例1

现在有一颗5阶B树，插入了1,2，5,8，再插入一个元素10，该节点会满

取1,2，5,8，10中间关键字5,5向上，两边分裂

示例2

如图，再插入一个关键字40，会满

取18向上一级，两边分裂

4.删除

4.1 删除非终端关键字

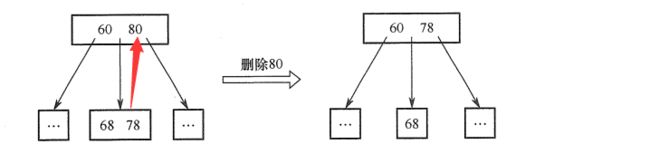
当被删除的关键字k不是终端节点时，可以用k的前驱或者后继节点k’来代替k，然后再删除k’，关键字k’必定在终端节点中，因此，删除非终端节点变成了删除终端节点！

删除80，先让其前驱78代替80，然后再根据规则删除终端节点78即可

4.2 删除终端关键字

分为三种情况

4.2.1 无需改动

删除后满足定义，也就是节点关键字个数大于等于m/2，直接删除即可

以5阶B树为例，如果某个节点删除关键字后，其关键字个数仍然大于等于2，不用做调整

删除3，该节点关键字个数为2，直接删除即可

4.2.2 兄弟够借

其实逻辑很简单，仔细看下就明白了

兄弟够借：删除后关键字个数小于m/2，但兄弟节点关键字个数借你一个后，其仍满足大于等于m/2

方法：父子换位法

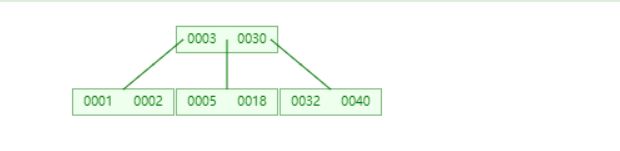
示例1 借右兄弟

删除12，只有9一个关键字了，不符合B树的特点了，但是其右兄弟有3个关键字，借一个出去还剩两个，仍然满足特点，也即兄弟够借

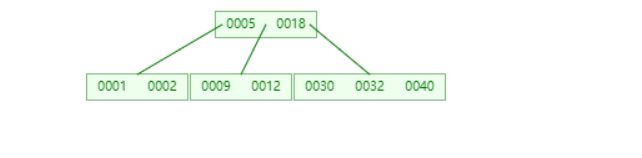
采用父子换位法，让兄弟节点的关键字（可以看到是最左边的）上去，父节点关键字（可以看到是父节点最右边的关键字）下来合并

示例2 借左兄弟

删除9，不满足性质，但左兄弟够借

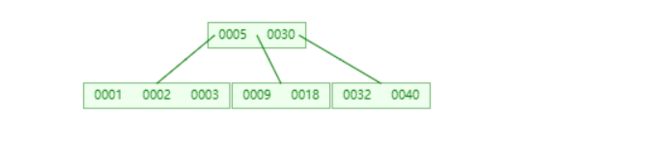
父子换位法，3上去，5下来合并

4.2.3 兄弟不够借

兄弟不够借：删除后关键字个数小于m/2，兄弟节点关键字个数只有m/2个，无法借给你

方法：父子合并法

示例1

删除5，不满足B树性质，兄弟也无法借

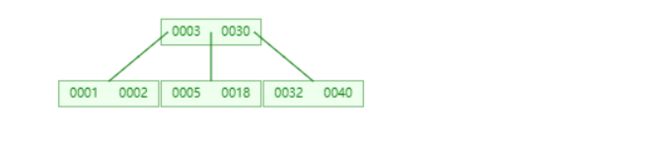
18和左兄弟合并，但是此时，根节点有两个关键字，但是只有两个子树，不符合B树性质，于是父节点的关键字3（为了保持性质必定会下来）下移合并

示例2

删除5，兄弟都不够借

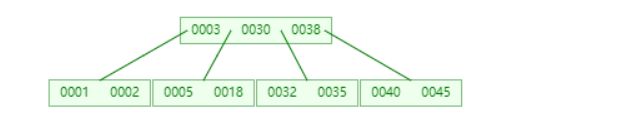
与左兄弟合并，父节点3下来（为了保持性质必定会下来），父子合并

二.B+树

对于一个m阶B+树

• 任何节点最多m棵子树（子树数量 = 节点关键字数量）
• 根节点关键字数量：1 <= n <= m
• 非根节点关键字数量：⌈ m/2⌉ <= n <= m
• 所有叶节点包含全部关键字以及对应记录的指针（数据）
• 分支节点仅包含下一级的各个子节点的最大值（不包含数据）

B+树查找、插入、删除与B树基本类似。不过在查找时，非叶节点的值等于给定值时，不会停止，而是直到找到叶节点上的关键字为止。所以，在B+树中，无论是否查找成功，每次查找都是一条从根节点到叶节点的路径

三.关于B+树的面试题

1.为什么使用B+树不用B树？

（1）B+树的磁盘读写代价更低

假设我们上图的主键是bigint类型，长度为8字节，InnoDB指针一般为6字节，那么主键+指针一共14节点，而一页有16k=16384字节，所以一页可以有16384/14=1170个主键+指针结构，那么一刻高度为2的B+树的叶子节点可以有1170个，实际开发中一条记录一般为1k，也就是说一页可以放16条数据，那么总共可以放1170*16=18720条记录，所以使用B+的存储能力还是挺强的，同理高度为3的B+树可以存放219024000条记录，所以高度为1-3的B+树就可以存放千万条记录

B树不管非叶子节点还是叶子结点，都会保存数据，这样导致非叶子节点能保存的指针变少，所以想要保存大量数据，只能增加树的高度，而在查询数据时，一般根节点是常驻内存的，一次页的查找代表一次IO，所以B+树的IO次数少，性能好

（2）查询稳定

B+树在查找时，非叶节点的值等于给定值时，不会停止，而是直到找到叶节点上的关键字为止。所以，在B+树中，无论是否查找成功，每次查找都是一条从根节点到叶节点的路径，导致每一个数据的查询效率相当

（3）适合范围查询

B+树只需要去遍历叶子节点就可以实现整棵树的遍历。而且在数据库中基于范围的查询是非常频繁的，而B树不支持这样的操作或者说效率太低

2.为什么使用B+树不用红黑树或者平衡树？

1.红黑树常用于存储内存中的有序数据，不适合存储数据库表大数据

2.即使你找到了把红黑树存进硬盘的方法，红黑树查找一个节点最多要查logn层，每一层都是一个内存页，要启动logn次磁盘IO！！！

3.为了解决二叉树数据有序时出现的线性插入树太深问题，平衡树的深度会明显降低，虽然极大提高性能，但是当数据量很大时，树的深度依旧非常大，mysql读取时会消耗大量IO

3.为什么数据库要有主键？

因为 InnoDB 表里面的数据必须要有一个 B+tree 的索引结构来组织、维护我们的整张表的所有数据，从而形成 .idb 文件

4.为什么推荐使用整型自增？

首先整型的占用空间会比字符串小，而且在查找上比大小也会比字符串更快。字符串比大小的时候还要先转换成 ASCII 码再去比较。如果使用自增的话，在插入方面的效率也会提高

不使用自增，可能时不时会往 B+tree 的中间某一位置插入元素，当这个节点位置放满了的时候，节点就要进行分裂操作(效率低)再去维护，有可能树还要进行平衡，又是一个耗性能的操作

都用自增就会永远都往后面插入元素，这样索引节点分裂的概率就会小很多