【计算机视觉】基于SIFT特征的校园建筑物匹配与视频流时序还原

计算机视觉之特征点检测与匹配

**角点检测(Corner Detection)**是计算机视觉系统中用来获得图像特征的一种方法，广泛应用于运动检测、图像匹配、视频跟踪、三维建模和目标识别等领域中。也称为特征点检测。

角点通常被定义为两条边的交点，更严格的说，角点的局部邻域应该具有两个不同区域的不同方向的边界。而实际应用中，大多数所谓的角点检测方法检测的是拥有特定特征的图像点，而不仅仅是“角点”。这些特征点在图像中有具体的坐标，并具有某些数学特征，如局部最大或最小灰度、某些梯度特征等。

现有的角点检测算法并不是都十分的鲁棒。很多方法都要求有大量的训练集和冗余数据来防止或减少错误特征的出现。角点检测方法的一个很重要的评价标准是其对多幅图像中相同或相似特征的检测能力，并且能够应对光照变化、图像旋转等图像变化。

1.Harris角点检测算法

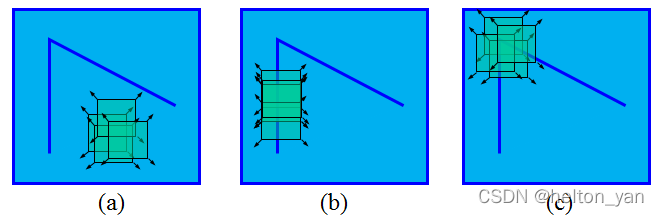
对于Harris角点而言，当一个窗口在图像上移动，在平滑区域如图(a)，窗口在各个方向上没有变化。在边缘上如图(b)，窗口在边缘的方向上没有变化。在角点处如图©，窗口在各个方向上具有变化。Harris角点检测正是利用了这个直观的物理现象，通过窗口在各个方向上的变化程度，决定是否为角点。

更为详细的关于Harris角点数学原理的介绍，以及如何基于C++代码实现Harris角点的提取，可以参考我之前写的一篇博客，这里不再赘述：【理解】经典角点检测算法–Harris角点

下面我将使用Python OpenCV内置的Harris角点提取函数进行图像Harris角点检测：

# Harris角点提取
def extraHarrisfromImg(img, threshold):
    if img.ndim == 3:
        img = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)    
    img = np.float32(img)
    # opencv函数计算响应值
    dst = cv2.cornerHarris(img, 2, 3, 0.04)
    # 实际阈值
    threshold = threshold*dst.max()
    # 大于阈值的设为角点
    cor_axis = np.array(np.where(dst > threshold)).T[:,[1,0]]
    # 返回角点坐标
    return cor_axis

当然，提取了角点以后，我们还需要对角点在图像中的分布进行可视化，因此同样需要定义一个角点可视化函数：

# 可视化角点
def drawCor(img, cors):
    red = (0,0,255)
    gre = (0,255,0)
    yel = (0,255,255)
    
    if cors.shape[1] == 4:
     	... ...
    else:
        for cor in cors:
            #绘制角点
            x0, y0 = int(round(cor[0])), int(round(cor[1]))
            cv2.circle(img, (x0, y0), 5, yel, 1, lineType=cv2.LINE_AA)

然后我们便可以在主函数中定义Harris角点提取流程，值得注意的是，这里用到的有关utils库中的函数均是本人自定义的函数，具体实现已经在上一篇博客中给出，这里便不再赘述：https://blog.csdn.net/SESESssss/article/details/123539440。

    data_root, result_root = './datasets/', './cor_info/'
    img_path, img_name = utils.read_img_files(data_root)
    img1 = cv2.imread(img_path[3])
    img1,_,_ = utils.auto_reshape(img1, 820)
    harris_cors = extraHarrisfromImg(img1, 0.1)
    print(harris_cors.shape)
    drawCor(img1, harris_cors)

(5596, 2)

(3365, 2)

(586, 2)

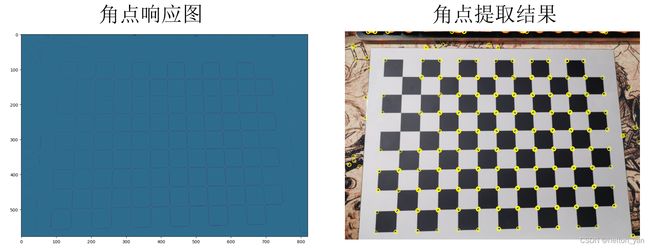
Harris角点提取结果以及响应图可视化：

如上图所示，右侧为直观的图像中的Harris角点，左侧为图像的Harris角点响应值，值越大(越亮的区域)被认为是角点的概率也越大。

为了能够在特点的任务下灵活的选取角点的数量，Harris角点需要设置一个阈值，当角点响应图中的像素值大于该阈值时，才被认为是角点，接下来可视化不同阈值下的图像Harris角点分布：

注意，实际的阈值和传入的阈值T有所不同。这里阈值的计算公式为 threshold = T*max(dst)

因此实际的阈值实则和图像的最大响应程度有关，Harris角点的阈值对于不同的图像具有一定的自适应性。

再看一组结果(相机标定板)：

2.SIFT角点检测算法

SIFT即尺度不变特征转换(Scale-invariant feature transform)

是一种电脑视觉的算法用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量，此算法由 David Lowe在1999年所发表，2004年完善总结。

其应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对。此算法有其专利，专利拥有者为英属哥伦比亚大学。局部影像特征的描述与侦测可以帮助辨识物体，SIFT 特征是基于物体上的一些局部外观的兴趣点而与影像的大小和旋转无关。对于光线、噪声、些微视角改变的容忍度也相当高。基于这些特性，它们是高度显著而且相对容易撷取，在母数庞大的特征数据库中，很容易辨识物体而且鲜有误认。使用 SIFT特征描述对于部分物体遮蔽的侦测率也相当高，甚至只需要3个以上的SIFT物体特征就足以计算出位置与方位。在现今的电脑硬件速度下和小型的特征数据库条件下，辨识速度可接近即时运算。SIFT特征的信息量大，适合在海量数据库中快速准确匹配。

使用VLFeat开源库进行SIFT特征提取

链接：VLFeat - Home

下载vlfeat-0.9.21-bin.tar.gz后解压到指定目录，将\vlfeat-0.9.21\bin\win64目录添加到系统的环境变量中，便可以在命令行调用vlfeat库中的sift特征提取功能。

其他系统对应环境变量配置路径：

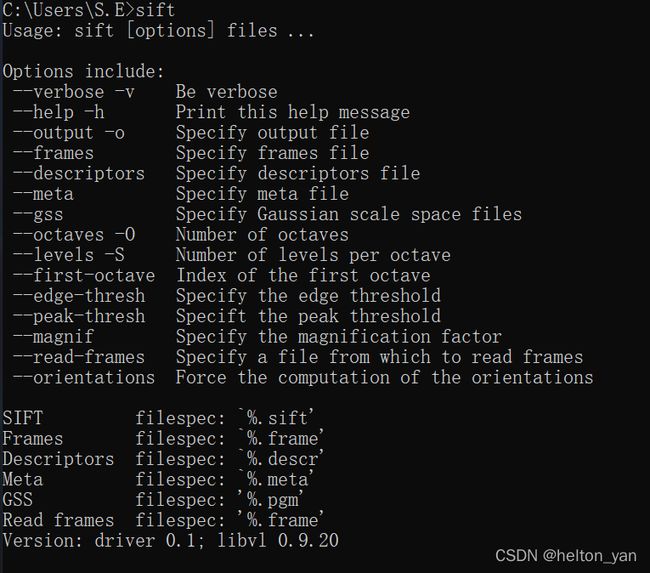
设置环境变量后，终端输入sift，出现以下提示信息则配置成功：

根据所给提示命令，我们可以利用命令行对一张图像进行sift特征的提取，如下：

sift [img_file] --output=[output_file] --edge-thresh 10 --peak-thresh 5

其中--edge-thresh 和--peak-thresh是较为常用的两个参数：

peak参数越大，算法越能够过滤掉在DOG尺度空间中图像特征下响应程度较小的极值点

edge参数越小，越能够过滤掉DOG尺度空间中曲率越小的极值点(越容易是边缘的特征点)

根据实际需求可以进行灵活的调节。

由于每次特征提取都需要在命令行中重复执行一次命令，利用python的os库可以将执行命令行中的命令封装为函数，简化过程，有利于后期进行大批量图像的处理。同时，由于vlfeat库中的sift特征只接受格式为.pgm的灰度图像，因此每次输入一张三通道RGB图像时，需要将其转化为灰度图，并另存为：

def extraSIFTfromImg(src_name, src):
    # 转化为灰度图
    im = cv2.cvtColor(src, cv2.COLOR_RGB2GRAY)
    # 灰度图另存为
    img_name = 'tmp.pgm'
    cv2.imwrite(img_name, im)
    dst_name = src_name + '.sift'
    cmd_param = ' --edge-thresh 10 --peak-thresh 5'
    command = 'sift ' + img_name + ' --output=' + dst_name + cmd_param 
    # 执行命令行命令
    os.system(command)

利用一张图像试试水：

    img = cv2.imread('home.jpg')[:,:, [2,1,0]]
    # 图像reshape
    img, h, w = utils.auto_reshape(img, 1080)
    extraSIFTfromImg('home', img)

提取后的特征将会以文本文件的格式保存。

如果我们需要将文本文件以二进制数据读取，可以定义一个读取函数：

# 读取文本文件中的SIFT特征并转化为numpy数组
def txt2SIFT(name, root='./c/'):
    cors = open(root+name+'.sift','r').readlines()
    x, y, scale, direction, desc = [], [], [], [], []
    for cor in cors:
        cor = cor.split(' ')[:-1] # 去除掉换行符
        x.append(float(cor[0]))          # 坐标x
        y.append(float(cor[1]))          # 坐标y
        scale.append(float(cor[2]))      # 尺度
        direction.append(float(cor[3]))  # 方向
        desc.append([int(i) for i in cor[4:]]) # 描述子
    cors_info = np.array([x,y,scale,direction]).T
    desc = np.array(desc)
    return cors_info, desc

问题&解决：

在这一步很有可能会遇到提取的特征文件为空的情况，这是由于0.9.21版本太新导致的，可以尝试安装之前的老版本(本人用的是20)。

参考了这一篇博客，顺利解决：vlfeat0.9.21提取sift特征为空

最终提取的角点文件格式如下：

每一行代表一个特征点信息，前两列表示角点位于图像中的坐标，第三列代表特征点是在何种尺度下被提取的，第四个参数代表特征点的旋转角度，即梯度的主方向。

在每一行之后的128列就是每个特征点对应的描述子

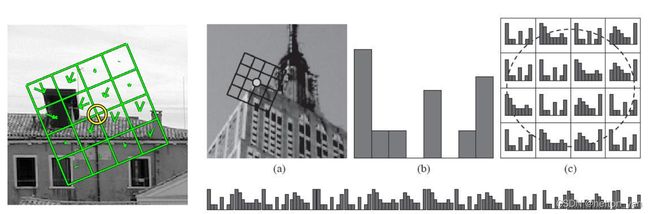
为什么是128维：SIFT算法以特征点为中心的周围4x4的网格区域，在每个区域中独立的计算区域梯度分布(八个方向,4x4x8=128。如下图所示：

SIFT特征可视化：

由于SIFT特征具有旋转以及尺度不变性，因此在可视化过程中，我们可以将特征点的尺度以及方向角清晰的表示出来：

# 可视化角点
def drawCor(img, cors):
    red = (0,0,255)
    gre = (0,255,0)
    yel = (0,255,255)
    
    if cors.shape[1] == 4:
        for cor in cors:
            θ = cor[3]             # 方向
            r = int(round(cor[2])) # 尺度
            x0, y0 = int(round(cor[0])), int(round(cor[1])) # 坐标
            x1, y1 = int(round(x0 + r*np.cos(θ))),  int(round(y0 + r*np.sin(θ)))
            # 绘制角点
            cv2.circle(img, (x0, y0), r, gre, 1, lineType=cv2.LINE_AA)
            cv2.line(img, (x0,y0), (x1, y1), red, 1, lineType=cv2.LINE_AA)
    else:
		... ...
    cv2.imwrite('corner.png', img)

以一张图像为例：

    data_root, result_root = './datasets/', './cor_info/'
    # 批量提取sift特征
    # extractBatchSIFTs(data_root, result_root)
    img_path, img_name = utils.read_img_files(data_root)
    img1 = cv2.imread(img_path[0])
    img1,_,_ = utils.auto_reshape(img1, 1080)
    sift_cors, desc = extraSIFTfromImg(img1, img_name[0])
    print(sift_cors.shape)
    drawCor(img1, sift_cors)

(1603, 4)

可视化结果：

如图所示，绿色圆圈的半径表示了该特征点的尺度，红色的指针表示其方向(可以发现SIFT有时会多次提取同一个特征点，区别在于特征点的方向不同，一个是主方向，其余的是辅方向)

SIFT特征与Harris特征对比

img1 = cv2.imread('./corner.png')[:,:,[2,1,0]]
img2 = cv2.imread('./corner0.png')[:,:,[2,1,0]]
imgs = {'SIFT edge=5 peak=10':img1,'Harris T=0.5':img2,}
utils.view_contrast(imgs)

可以看到Harris只会关注那些边角区域的真实的角点，而SIFT也会关注平滑区域中心那些显著不变的点。

图像间的SIFT特征点匹配

利用SIFT特征的梯度描述子，我们可以基于余弦相似度对两幅图像间的特征点进行匹配：

值得注意的是，原始SIFT描述子是未归一化的，为了消除量纲的影响，我们需要先对描述子进行标准化(即向量除以其模长)

# 行数据标准化
def norm(x):
    return x / np.linalg.norm(x,axis=1).reshape(-1,1)

接着我们可以定义一个匹配函数：

# 描述子单向匹配
def singleMatch(norm_desc1, norm_desc2):
    match_seq = []  # 匹配序列
    # 计算余弦距离
    sim_matrix = norm_desc2 @ norm_desc1.T
    sim_matrix = sim_matrix.T # 相似矩阵
    # 可视化相似矩阵
    # plt.imshow(sim_matrix)
    # plt.show()
    # 从大到小顺序排列
    sim_idx = np.argsort(sim_matrix, 1)[:,::-1]
    for i in range(sim_idx.shape[0]):
        top1_idx, top2_idx = sim_idx[i,0], sim_idx[i,1]
        top1_val = sim_matrix[i,top1_idx]
        top2_val = sim_matrix[i,top2_idx]
        # 最近邻角度/第二近邻角度<阈值 ? 是匹配点 : 舍弃
        if np.arccos(top1_val) < 0.6 * np.arccos(top2_val):
            match_seq.append([i, top1_idx])
        else:
            match_seq.append([i, -1])

    return np.array(match_seq)

其中代码里的这句话：

        # 最近邻角度/第二近邻角度<阈值 ? 是匹配点 : 舍弃
        if np.arccos(top1_val) < 0.6 * np.arccos(top2_val):

这段代码的意义在于，保证匹配的点对之间是充分匹配的(第二相似的匹配点与之的余弦距离要充分大于第一相似的点)，阈值0.6是可变的，定义了充分的程度。

值得注意的是，为了保证匹配点对的可靠性，在匹配过程中我们还需进行双向匹配，即img1中的点一一匹配img2的所有点，同样的img2中的点也需一一匹配img1中的所有点：

# 描述子双向匹配
def doubleMatch(desc1, desc2):
    # 标准归一化
    norm_desc1 = norm(desc1)
    norm_desc2 = norm(desc2)
    # 双向匹配
    matches_12 = singleMatch(norm_desc1, norm_desc2)
    matches_21 = singleMatch(norm_desc2, norm_desc1)
    matcher = []
    for i in range(matches_12.shape[0]):
        if(matches_12[i,1] != -1): # 排除掉无匹配的点
            # 若双向匹配是对称的，才是合格的匹配点
            if matches_21[matches_12[i,1], 1] == matches_12[i,0]:
                matcher.append([matches_12[i,0], matches_12[i,1]])
    return np.array(matcher)

待匹配的图像对SIFT特征可视化：

SIFT特征匹配效果：

效果十分可观。

不过，对于空间变换较大的图像对，SIFT就显得有些无能为力，匹配点对明显下降并出现了一定的错配点对。

3.实战 校园建筑物匹配

大体的思路同上，不过我们需要新定义几个函数，方便批量处理：

涉及的过程比较繁琐，这里不再对代码进行一一解释。

批量提取图像SIFT特征

# 批量提取图像SIFT特征
def extractBatchSIFTs(data_root, result_root):
    img_path, img_name = utils.read_img_files(data_root)
    for i in range(len(img_path)):
        img = cv2.imread(img_path[i])
        img, _, _ = utils.auto_reshape(img, 1080)
        extraSIFT2txt(img, img_name[i], result_root)

批量进行图像SIFT特征匹配

# 匹配与当前图像最相似的帧(用于拍摄时序还原)
def matchImgViz(data_root, result_root, downsample=False):
    img_path, img_name = utils.read_img_files(data_root)
    small_data_root = 'D:/YHT/学习/大三下/computer_vision/exp2/datasets_small/'
    if(downsample):
        for i in range(len(img_path)):
            img = cv2.imread(img_path[i])
            img,_,_ = utils.auto_reshape(img, 200)
            cv2.imwrite('./datasets_small/' + img_name[i]+'.png', img)
            print(small_data_root + img_name[i]+'.jpg')
    
    match_matrix = np.load('match_matrix.npy')
    g = pydot.Dot(graph_type='graph')
    for i in range(match_matrix.shape[0]-1):
        g.add_node(pydot.Node(str(i), shape='rectangle', image=small_data_root + img_name[i]+'.png'))
        for j in range(i+1,match_matrix.shape[0]):
            if(match_matrix[i,j]>1):
                print(small_data_root + img_name[i]+'.png')
                g.add_node(pydot.Node(str(j), shape='rectangle', image=small_data_root + img_name[i]+'.png'))
                g.add_edge(pydot.Edge(str(i), str(j)))
    g.write_png('graph.jpg')

其中值得注意的是，代码中会用到Pydot模块，由于Pydot依赖Graphviz库，若直接使用pip安装，可能会出现环境错误。最好通过下面提供Graphviz库的下载链接：Download | Graphviz 进行下载。

我下载的版本是graphviz-2.50.0

数据采集

本次匹配数据本人通过手机共采集了校园内各处优美的风景以及极具嘉庚建筑特色的教学楼和行政楼共计30张(顺便宣传一波集大优雅的校园环境)

提示：若参数设置不当，匹配过程可能十分漫长

匹配结果可视化

不难发现，仍然存在些许匹配错误的建筑，一个很主要的原因便是，两帧图像之间的空间变换关系太明显。这是因为SIFT描述子的尺度以及旋转不变性并不能很好的适应尺度较大的透视变换。

4.实战 视频流时序还原

基于上面的结论，我们不妨再试试SIFT特征对于小尺度变换下的图像匹配任务的鲁棒性。一个有意思的实现便是，对于n帧拆分成图像并且打乱顺序的视频流，我们可以利用SIFT特征对这些乱序的帧进行时序上的还原。

由于每张图像只会匹配与之相对应最类似的帧作为相邻帧，因此匹配函数需要稍微改动下：

# 批量进行图像SIFT特征匹配
def matchBatchImgs(data_root, result_root, extraSIFT=False):
    if extraSIFT:
        extractBatchSIFTs('./datasets/', './cor_info/')
    img_path, img_name = utils.read_img_files(data_root)
    img_nums = len(img_name)
    # 获取该批图像的所有描述子:
    desc_list = []
    for i in range(img_nums):
        _, desc = txt2SIFT(img_name[i], result_root)
        desc_list.append(desc)
    # 两两进行匹配：
    match_matrix = np.zeros((img_nums, img_nums))
    for i in tqdm(range(img_nums-1), desc='Processing'+str(i)):
        j=i+1
        for j in tqdm(range(i+1, img_nums), desc='Processing'+str(j)):
            matches = doubleMatch(desc_list[i], desc_list[j])
            match_matrix[i,j] = matches.shape[0]
    # 可视化匹配矩阵
    origin_matrix = match_matrix
    plt.imshow(match_matrix)
    plt.show() 
    # 下面这段代码删除无匹配点的矩阵行
    zero_rows = []
    for i in range(img_nums):
        if(sum(match_matrix[i,:]) == 0):
            zero_rows.append(i)
    match_matrix = np.delete(match_matrix, zero_rows, axis=0)
    # 匹配索引矩阵:
    match_idx_matrix = np.argsort(match_matrix, 1)[:,::-1]
    match_sort_matrix = np.sort(match_matrix, 1)[:,::-1]
    # 将那些0匹配的图像对设为-1，不再考虑
    match_idx_matrix[match_sort_matrix==0] = -1
    # 输出匹配图像的名称(无向图)
    match_img_name = {}
    for i in range(match_idx_matrix.shape[0]):
        names = []
        for idx in match_idx_matrix[i,:]:
            if idx == -1:break
            names.append(img_name[idx])
        match_img_name[img_name[i]] = names
    print(match_img_name)
    return origin_matrix# match_matrix   # 无向图邻接矩阵

数据采集

通过相机环绕物体(我的鞋)一周的连续图像帧，将其乱序处理：

匹配结果可视化

匹配的结果能够还原原有的时序：

没了