(一)卡尔曼滤波算法简介
卡尔曼滤波算法简介
- 1.卡尔曼滤波器--最优状态估计
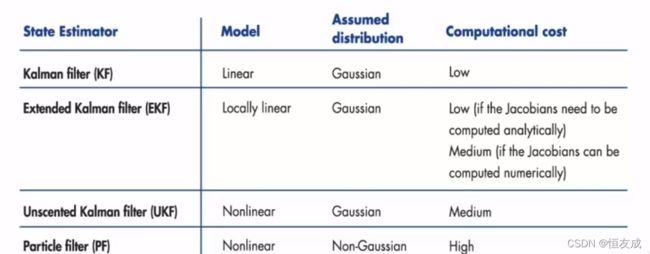
- 2.非线性系统
-
- 2.1扩展卡尔曼滤波器EKF
- 2.2 无迹卡尔曼滤波器UKF
- 2.3 粒子滤波器
- 3.总结
参考自B站MATLAB中国及《视觉SLAM十四讲》第9章9.1
1.卡尔曼滤波器–最优状态估计
假如有一个自动驾驶汽车比赛,要求参赛汽车根据GPS测量定位分别在100种地形上行驶1公里,在每种地形上都尽量停靠在1公里终点处。计算100次的平均最终位置,取位置方差最小且平均位置最接近1公里的队伍获胜。
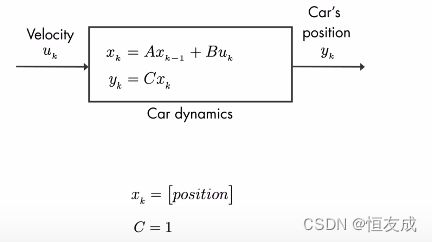
GPS的定位是比较粗糙的,误差较大,为了赢得比赛,期望获得尽量准确的位置估计。一个汽车系统可以简化成如下形式,输入是油门,输出是位置。
上式中: μ k \mu_k μk是速度, x k x_k xk是预测量, y k y_k yk是测量量。
理想情况下测量值等于预测值,因此 y k = x k y_k=x_k yk=xk,因此 C = 1 C=1 C=1。为了让汽车停靠位置尽量靠近终点,因此必须得到尽可能准确的 y y y。
实际场景还需考虑噪声,对于测量量 y k y_k yk,使用GPS测量时难免会有测量误差,记为 v k ∼ N ( 0 , R ) , R = σ v 2 v_k\sim N(0,R),R=\sigma _v^2 vk∼N(0,R),R=σv2。同样对于预测变量 x k x_k xk,因 x k x_k xk与速度有关,速度有可能受风速等的影响,必须考虑这个过程噪声,记为 ω k ∼ N ( 0 , Q ) , Q = σ ω 2 \omega_k \sim N(0, Q),Q=\sigma _ \omega^2 ωk∼N(0,Q),Q=σω2。虽然不能准确的确定噪声的具体值,但可以知道噪声值的概率分布服从高斯分布。

上述介绍的是实际的汽车动力学模型,这个模型我们是不知道的,只能根据假设的模型来预测计算。
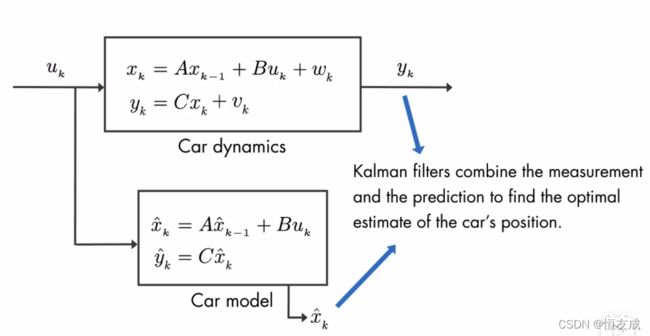
这里如何根据带有噪声的测量量和有噪声的预测量来尽可能准确的估计汽车的真实位置,正是kalman滤波可以做的事情。
如上图, k − 1 k-1 k−1时刻的估计位置 x ^ k − 1 \hat{x}_{k-1} x^k−1方差较小,预测位置的不确定性较小,到了第 k k k时刻,预测值 x ^ k \hat{x}_k x^k的不确定性变大,测量值 y k y_k yk的不确定性相对较小,将预测量与测量量概率分布相乘,得到新的高斯分布,取其均值作为汽车在 k k k的位置是比较准确的。
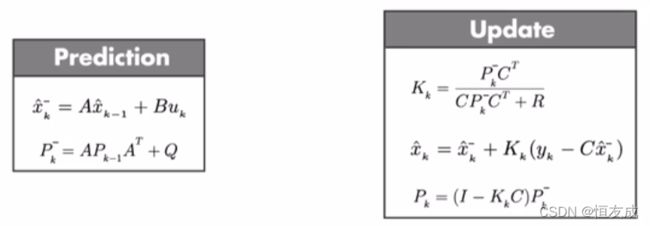
预测量与测量量概率密度函数的乘法与如下所示的离散Kalman滤波方程有关,
x ^ k = A x ^ k − 1 + B μ k + K k ( y k − C ( A x ^ k − 1 + B μ k ) ) \hat{x}_k = A\hat{x}_{k-1} +B\mu_k+K_k(y_k-C(A\hat{x}_{k-1} +B\mu_k)) x^k=Ax^k−1+Bμk+Kk(yk−C(Ax^k−1+Bμk))
卡尔曼滤波器是为随机系统设计的状态观测器。
上述方程的第一部分表示为 x ^ k − \hat{x}_k^- x^k−,取决于 k − 1 k-1 k−1时刻的输出 x ^ k \hat{x}_k x^k和 k k k时刻的输入 μ k \mu_k μk,如下图:

x ^ k − \hat{x}_k^- x^k−部分取决于先前时刻的位置估计和当前的速度,因此也称为先验估计。借助 x ^ k − \hat{x}_k^- x^k−,可将 x ^ k \hat{x}_k x^k表示为:
x ^ k = x ^ k − + K k ( y k − C x ^ k − ) \hat{x}_k = \hat{x}_k^- +K_k(y_k-C\hat{x}_k^-) x^k=x^k−+Kk(yk−Cx^k−)
从上式可以看到第二部分使用的是测量量, K a l m a n Kalman Kalman滤波方程由预测值和基于测量量的更新值组成, K k K_k Kk称为Kalman 增益系数, x ^ k \hat{x}_k x^k称为后验估计。如下图:
题外话:关于先验估计与后验估计,可以根据字面意思理解。先验估计顾名思义就是借助先前的经验来估计,譬如1枚硬币,在扔出去之前根据经验就可以估计出来出现正面的概率是1/2。后验估计,就是要通过测量试验后才能进行的估计,譬如已知一个箱子里装了红黑两种颜色的球,但是不知两种球的比率,学过概率后都知道可以从箱子中取样,样本中红黑球的比率可当作箱子中红黑球的比率,这种通过试验来进行的估计就是后验估计。
回过来说汽车的例子,汽车位置估计的卡尔曼方程的先验估计和更新部分可表示为
还记得Q和R分别是过程噪声和测量噪声的方差,P表示的是预测值的协方差,对于单变量系统,其对应的是方差。卡尔曼增益 K K K用来调整预测值和测量值在状态估计时所在的比例,当预测值较准确时,希望 x ^ k − \hat{x}_k^- x^k−占比大些,当测量时准确时,希望 y k − C x ^ k − y_k-C\hat{x}_k^- yk−Cx^k−所占的比例大些。
观察卡尔曼增益 K K K的表达式,当测量误差趋近于0时, R R R趋近0,可以得到估计值等于测量值,测量值的概率密度函数将变成1个脉冲值,其对应的位置就是最优估计。
再考虑当 P P P趋近于0时,此时卡尔曼增益也等于0,预测值完全取决于先验估计,与测量值无关。
卡尔曼滤波进行状态估计,并不需要所有的先验信息,只需 k − 1 k-1 k−1时刻的预测估计,不断进行更新即可。
从前面描述中可以看到测量值是基于 G P S GPS GPS的,增加更多的传感器,如 I M U IMU IMU等可提高测量值的准确度,得到更准确的位置估计。观察卡尔曼方程,增加传感器时,只需要增加 y y y, K K K, C C C的维度即可。因此卡尔曼滤波器也被称为传感器融合算法。
2.非线性系统
第一部分介绍的简化后汽车模型的卡尔曼方程对应的是一个线性系统,实际中,更常见的是非线性系统,如汽车模型考虑摩擦,则预测值与速度的关系将变成非线性的。对应的测量函数也有可能与预测值之间是非线性的。
{ x k = A x k − 1 + B μ k + ω k y k = C x k + v k = > { x k = f ( x k − 1 , μ k ) + ω k y k = g ( x k ) + v k \left\{\begin{matrix} x_k = Ax_{k-1}+B\mu_k+\omega_k \\ y_k = Cx_k + v_k \end{matrix}\right.=>\left\{\begin{matrix} x_k = f(x_{k-1}, \mu_k)+\omega_k \\ y_k=g(x_k) + v_k \end{matrix}\right. {xk=Axk−1+Bμk+ωkyk=Cxk+vk=>{xk=f(xk−1,μk)+ωkyk=g(xk)+vk
在线性系统中,服从高斯分布的预测值和测量值经过线性运算后得到的估计值依然服从高斯分布:

而对于非线性系统得到的估计值将不再服从高斯分布,这将导致卡尔曼滤波器可能不收敛。

2.1扩展卡尔曼滤波器EKF
这里引出用于非线性系统的扩展卡尔曼滤波器(Extened Kalman Filter,EKF),EKF将非线性函数在 k k k时刻估算状态的平均值附近进行线性化,

使用EKF时有如下缺点:
- 1)导数复杂时,雅可比矩阵的解析解不易求得
- 2)使用数值解时,雅可比计算量较大
- 3)EKF仅适用于可微系统模型,系统模型不可微分时无法求雅可比矩阵,不能使用EKF
- 4)对于高度非线性系统,EKF的结果不是最优的
- 5)对于系统某些不能线性近似的状态,EKF表现较差
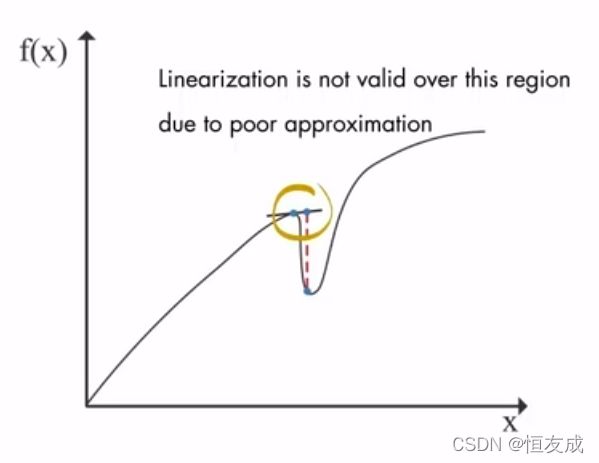
2.2 无迹卡尔曼滤波器UKF
由于EKF中使用了非线性函数的线性近似,存在诸多问题,而无迹卡尔曼滤波器(Unscented Kalman Filter,UKF) 通过近似预测量和测量量的概率分布而非近似非线性函数来进行状态估计。无迹卡尔曼滤波器在原概率分布上选择一组最小的采样点,使采样点的均值和方差与原概率分布相同,然后将每个采样点代入非线性函数进行计算得到输出点的均值和方差。根据输出点来计算高斯分布。

2.3 粒子滤波器
粒子滤波器(Particle Filter,PF),粒子滤波器近似任意分布,而不像UKF仅局限于高斯分布,为了估计任意的概率分布,粒子滤波器所需的采样点远远大于UKF。

3.总结
1.https://www.bilibili.com/video/BV1V5411V72J?p=6&spm_id_from=pageDriver
2.https://book.douban.com/subject/27028215/