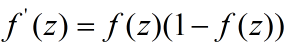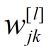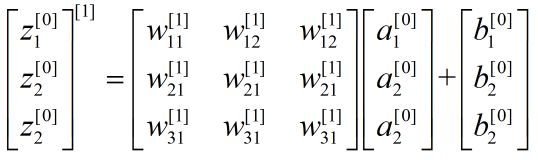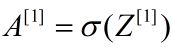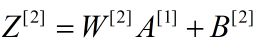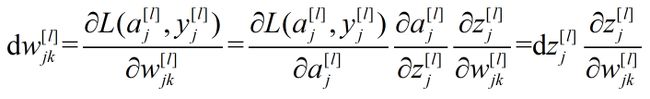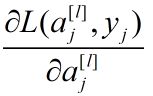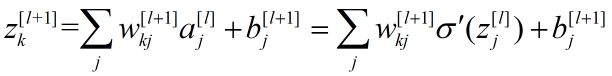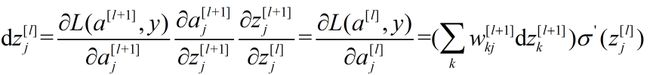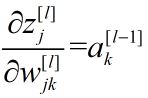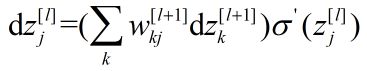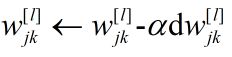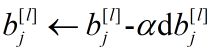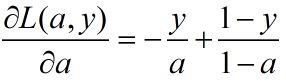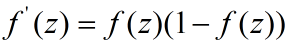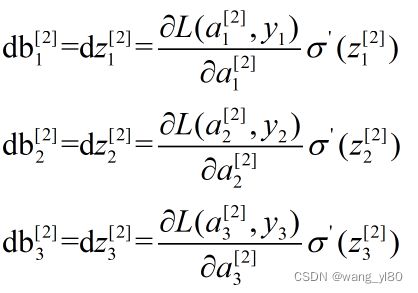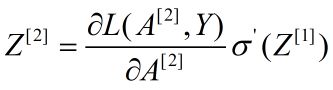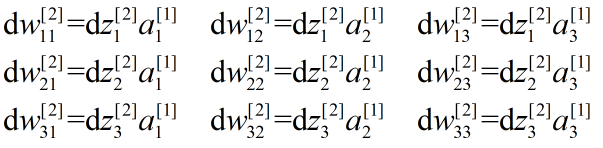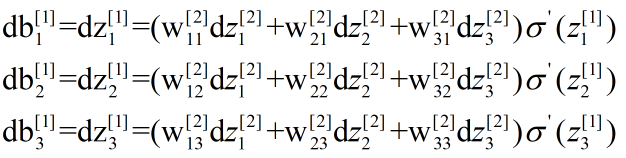BP神经网络学习总结

目录

0前言

1 神经网络

2 BP神经网络

3正向传播

4 反向传播

4.1损失函数和代价函数

4.2 梯度下降法

4.3 反向传播

 5 编程思路

6 应用

6.1 应用1-是猫吗？

6.2 应用2-识别手写字体

7 总结

---

0前言

由于工作上的需要或是探索，想起了神经网络，神经网络是我研究生毕业论文选用的一个工具，用来识别旋转机械振动故障类型。那时候觉得神经网络很难，反复看一本神经网络的书，硬生生的用VB把程序给编出来了，当时以为得之已，现在看只涂于表面。这次由于疫情被困酒店，所有的时间都用来学习，本人愚钝，整整用了七天才又一次用LabVIEW把BP网络程序编出来，较十五年前也有了更深的感悟。

参考资料：

1.《一文搞定BP神经网络——从原理到应用（原理篇）》一文搞定BP神经网络——从原理到应用（原理篇）_痴澳超的博客-CSDN博客_bp神经网络应用于https://blog.csdn.net/u014303046/article/details/78200010

CSDN上的一篇文章,浏览量最高的一篇博文，对BP网络公式的进行了详细的推导，细致入微，可能每个人对问题理解和阐述的角度不一样，加之文中有些符号意义没有标注，我是反复看了好多遍才深得其法，文章还提供了Python程序，便于理解各变量之间的关系，由于以前没用过Python，在解读程序上耗费了大量时间，通过这次学习，Python也算是入门了。本文对BP网络的阐述也基于此文，加之个人的理解，公式符号，变量名称也以此文为主，便于读者互相参考。

2.视频：网易公开课昆明理工大学刘辉主讲的《智能控制导论》第五章《人工神经网络》

智能控制导论-6.1 神经网络系统辨识-网易公开课https://open.163.com/newview/movie/free?pid=OGVF89EVA&mid=IGVF8A0ML&frm=record

 讲的比较浅显，便于理解反向传播过程的推导。

3.视频：网易公开课普林斯顿大学公开课《机器学习》吴恩达主讲

[中英字幕]吴恩达机器学习系列课程-普林斯顿大学公开课：领导能力简介(1)-网易公开课https://open.163.com/newview/movie/free?pid=BG8NLCHBE&mid=NGA5HMT7B

对反向传播从编程的角度用实例推演，便于理解。吴恩达是前百度首席科学家，人工智能和机器学习领域国际上最权威的学者之一，他还有个斯坦福大学讲课的公开视频，个人认为内容堪称经典。

吴恩达：机器学习-机器学习的动机与应用-网易公开课https://open.163.com/newview/movie/free?pid=IEU2H8NIJ&mid=VEU2H8NKA

4.从零零碎碎的文字中提及的参考资料，这两本书应当也不错：

《机器学习》，清华大学出版社，周志华

《PRML》，Springer，Bishop

以下内容按我自己的理解，讲述一下BP神经网络算法的推导及编程思路，有不妥之处欢迎指正。附LabVIEW程序及相关程序如下。

------------------------------------------------------------------------------------------

链接：https://pan.baidu.com/s/17JYW77A9uVrna5XCEdO3iA

提取码：9527

------------------------------------------------------------------------------------------

1 神经网络

神经网络顾名思义是模仿神经元传导信息的机制，其实神经网络难就难在“网络”上，单个神经元并不复杂，图1所示为单个神经元模型。有n个神经元将信息传递给当前神经元，神经元之间受连接权值w的作用，其中b是偏置节点，属于截距项，这些信息相加，共同作用的效果为z，z在神经元中受激活函数的作用后，形成新的信息y，再传递给其他神经元。神经元的信息来自多个神经元，也把信息传递给多个单元，最终形成了神经网络。

图1 典型神经元模型结构

激活函数的种类，以及为什么要用激活函数可参考此文:

神经网络中常用的几种激活函数的理解 - EEEEEcho - 博客园https://www.cnblogs.com/lliuye/p/9486500.html

简言之，如果没有激活函数，网络从前至后传导都是线性的，引入激活函数后就使神经网络有了非线性的特征。本文采用如下两个函数：

sigmoid函数：

 函数曲线如图2，可见0<f(z)<1，如果f(z)最末层神经元，那么输出就是就在(0,1)。

图2 sigmoid函数曲线

还有一个重要的公式需要记住，在反向传播的时候会用到，f(z)的导数为： 

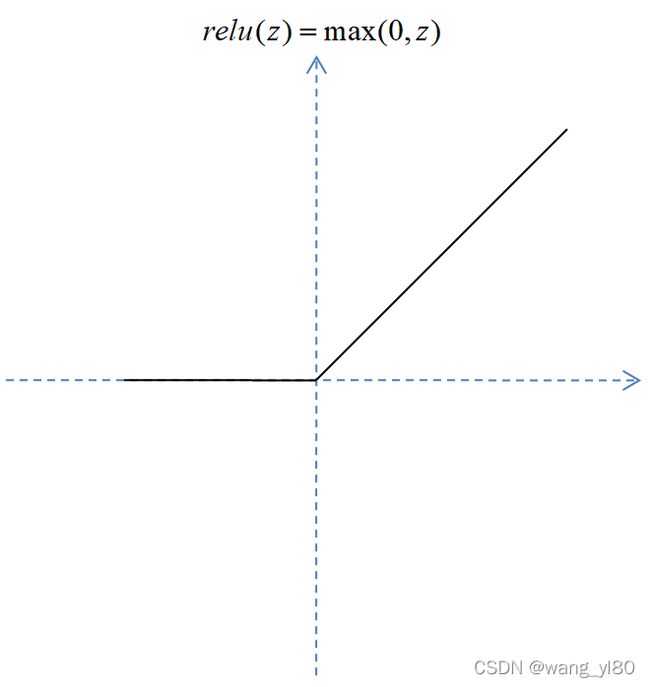
 relu函数：

 函数曲线如图3所示

图4 relu函数曲线

2 BP神经网络

如图5所示，BP神经网络在神经网络的发展中起着关键性作用，BP是反向传播back propagation的缩写，那么反向传播什么呢？即采用梯度下降法的误差反向传播，所以BP指的是神经网络的算法，这也是BP网络的精髓。

百度百科解释为：BP神经网络是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是应用最广泛的神经网络模型之一。所以图5所示标注为两层神经网络是不妥的。

图片来源于CSDN神经网络——最易懂最清晰的一篇文章_illikang的博客-CSDN博客_神经网络

图5 神经网络发展历史

BP网络使用前要经过训练和测试，训练的目的是确定各个神经元的连接权值w和截距b，通过正向传播和反向传播实现，训练的时候可以单个样本集逐一训练，也可以多个样本同时训练，训练完成后要拿新的样本进行测试，达到预期后就可以使用了，当然也可以边训练变使用。BP网络编程的时候要有矩阵运算的思想，矩阵是处理大数据的利器。

那么BP神经网络到底好用不好用，我个人之人只要特征值选的足够正确，训练样本足够多，准确率就足够高。

3正向传播

以图6所示示例来说明正向传播过程。

图6 BP神经网络模型示例

符号定义：

     ：样本输入

     [l]：第l层网络

   ：第l-1层第k个神经元向第l层第j个神经元传递的连接权值

     ：第l层第j个神经元的线性结果

..................................................................(1)

   ：第l层第j个神经元的输出值

........................................................................(2)

式(1)(2)即为正向传播的传导公式，根据公式可得

 定义大写字母加上标[l]表示矩阵，如,,,,,上式用矩阵形式表示为：

 看了这个矩阵知道为啥 中用表示当前神经元，表示上一层神经元了吧？就是为了用矩阵表述，一些资料反过来表示，我觉得有点误人子弟。整个式子写成矩阵：

上式可表示为：

 进一步计算：

 同理可得

 综上，知道了初始的 就可以逐层求解，得到最终输出，完成了正向传播。当网络中参量用矩阵表示时使整个过程也大大简化，MATLAB，Python，LabVIEW中都支持矩阵运算，给编程带来了很大的便利，当然如果你使用的语言没有矩阵运算功能，也可以编写矩阵计算的函数。

4 反向传播

引用参考资料1的表述：

反向传播的基本思想就是通过计算输出层与期望值之间的误差来调整网络参数，从而使得误差变小。反向传播的思想很简单，然而人们认识到它的重要作用却经过了很长的时间。反向传播算法产生于1970年，但它的重要性一直到David Rumelhart，Geoffrey Hinton和Ronald Williams于1986年合著的论文发表才被重视。

————————————————

版权声明：本文为CSDN博主「痴澳超」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。

原文链接：https://blog.csdn.net/u014303046/article/details/78200010

4.1损失函数和代价函数

显然未经过训练的网络计算的输出值是不准确的，我们需要一种方法通过训练样本来调整网络参数W和B值，使得样本的输出与期望值一致，定义一个输出值与期望值的误差函数，常用的函数有：

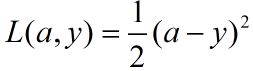.........................................................(3)

............................................(4)

式(3)是一个与绝对误差有关的函数，式(4)是一个极大似然函数，本文采用式(4)，对应一个样本的误差称为损失函数(Lost Function)，用L表示，为输出层所有神经元误差之和。

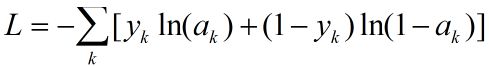 ​​​​.....................................(5)

多样本的误差称为代价函数(Cost Function)，用C表示，为所有样本误差的平均值，设样本数为m，则有：

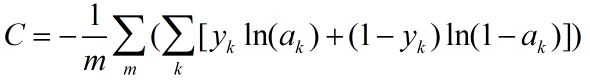..............................(6)

4.2 梯度下降法

有很关于梯度下降法介绍的资料，读者不清楚可自行脑补。讲真，让我阐述未必能讲明白，因为我自己就不是很明白。

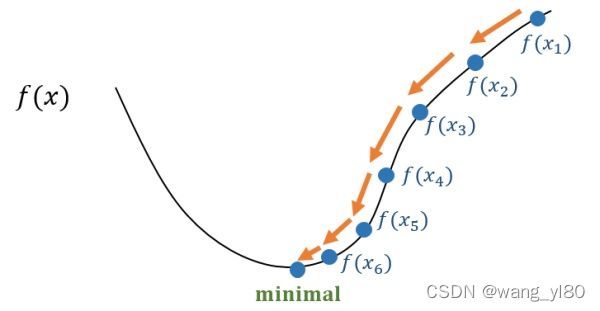
 图片来源：知乎-张磊梯度下降法-经典的优化方法梯度下降法 —— 经典的优化方法 - 知乎

图7 梯度下降法原理示例

回到BP

目标：使代价函数值最小，则输出与期望值一致

代价函数与A，Z，W，B有关系，调整W和B，调整值为dW，dB，代价函数就会相应的变化，如果按着负梯度变化趋势调节，最终可找到一点使代价函数的导数(梯度)值趋于0

所以综上所做的工作就是代价函数对W和B求偏导数，求dW，dB。

4.3 反向传播

为了便于理解，先不用矩阵表示，回归到单个神经元。

求解： 和

首先求

图8 求解单元示意图

…………………(7)

对于输出层：

…………………………(8)

 式(8)中 和 均可求出，所以已知。

 对于隐含层：

图9 隐含层计算

……………………(9)

由式(9)得：

…………………………….… (10)

利用式(7)可得

………….(11)

 注意式(11)中求和的含义与层每个神经元都有对应的，这个过程和正向传播刚好相反，如果用矩阵表示的话，须转置。

此外可求得：

…………………………...…………..(12)

综上：

…………………….…(13)

 式(7)只有来自后一层 未知，但最后一项已知，这样由后向前逐层计算就能求出每一层的dw。

下面求：

……………………… (14)

 综上，总结反向传播公式如下

(输出层) ………………………………… (8)

(隐含层) …………………………… (11)

………………………………………… (13)

……………………………………………… (14)

………………………………………… (15)

………………………………………… (16)

 下面利用这些公式根据图6所示的模型进行推演，方便理解各个变量之间的传递关系。

图6 BP神经网络模型示例

设：

误差采用最大似然函数

，则

 第2层激活函数为sigmoid，则

 第1层激活函数为relu，则

 为了便于表明前后层关系，激活函数的导数仍用 表示

第一步，求输出层

上式写成矩阵形式为：

上式写成矩阵形式为：

 第二步，求第1层

 上式写成矩阵形式为：

 

上式写成矩阵形式为：

通过推演，显然写成矩阵形式更简洁，也容易理解，总结反向传播编程所用的公式如表1所示。

 5 编程思路

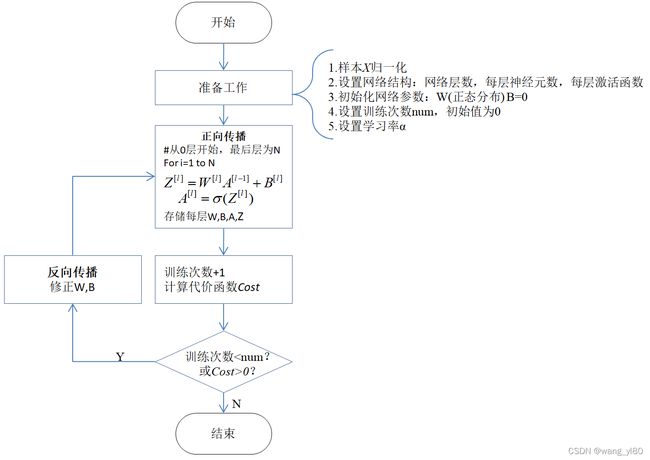
如果神经网络的算法弄明白了，编程应当不是件难事，图10所示为神经网络训练的流程图，图11所示为反向传播的流程图。

图10 网络训练流程图

图11 反向传播流程图

6 应用

6.1 应用1-是猫吗？

《一文搞定BP神经网络——从原理到应用（原理篇）》Python程序给出的例子是用BP网络来识别猫。

训练样本数：209

测试样本数：50

数据文件：.h5(模型文件)，存储图片数据(4维数组)和目标期望值。以训练数据为例说明数据格式，trainX为209×64×64×3，即209张图片，图片大小64×64像素，每个像素对应一个RGB颜色。trainY为209×1，即判断每张图片是否是猫，是1否0。

训练前需要把每个样本的图片数据转化成一维数据，即把64×64×3转化成12288×1，所以样本的输入层神经元数为12288，输出层神经元数为1，隐含层作者选择了选择了3层，每层神经元依次为20,7,5，最终网络结构为(12288,20,7,5,1)。

样本训练和测试前需要归一化，归一化是使各个输入单元的数值都在[-1,1]，归一化的好处很多而且是必要的，原因可参阅《归一化 （Normalization）、标准化 （Standardization）和中心化/零均值化 （Zero-centered）》归一化 （Normalization）、标准化 （Standardization）和中心化/零均值化 （Zero-centered） - 简书。

训练效果与学习率，训练次数、网络参数的初始化，网络结构有关，这些没有统一规定，只能根据实践探索。

图12 两次训练误差曲线

此例训练结束后，用50个样本测试，准确率约在80%左右，图13所示为识别错误的信息。值得强调的是可以利用当前的网络参数对测试样本再进行训练，这样会不断提高网络的计算精度。

图13判断错误的图片

6.2 应用2-识别手写字体

手机上的手写输入用的什么算法我不清楚，但是用BP网络识别毫无压力，识别文字原理和识别猫没有区别，而且当用户纠正识别错误文字时可以产生新的训练样本集，这样不但可以识别不同的字体还可以识别符合书写者习惯的字体。

识别手写字体太麻烦，编写了一个识别电子数字的程序，训练样本是没有缺陷的0-9的电子数字，然后识别有缺陷的样本，测试27个样本，只有4个识别错了，如图14所示，我们看一个识别的数据，如

索引3“0”：0.930，“9”：0.951，“8”：0.448，图形都很靠边。

图14 LabVIEW BP网络界面及识别错误的电子数字

7 总结

写完这篇总结已经是学习神经网络的第九天了，总结的过程中相当于又把知识巩固了一遍，所以总结很重要，分享也很快乐，希望我这篇文章能对你有所帮助或者是启发。

2022年4