Opencv学习笔记（十）霍夫直线检测

一、霍夫直线变换

1.数学原理

霍夫直线变换的核心在于笛卡尔坐标系和霍夫空间的变换，笛卡尔坐标系下的直线在霍夫空间中表示为点；笛卡尔坐标系下的点在霍夫空间中表示为曲线，如果霍夫空间中的多条曲线交于同一个点，则在笛卡尔坐标系中就表现为多个点组成了一条直线，这就给了我们找出图像中直线的方法——找出霍夫空间中多条曲线的交点。
笛卡尔坐标系到霍夫空间的变换实际上就是到极坐标系的变换。一条直线可以用斜截式表示为：$y=kx+b$（斜率$\infty$暂时不考虑），设原点到该直线的垂线与X轴正半周的夹角为${\theta }_0$，则由两垂线斜率互为负倒数的关系可以得到$k=-\frac{cos\theta }{sin\theta }$（此时若$k=\infty$,$\theta =0$即可）,再设直线距离为${\rho }_0$，则可以得到$b=\frac{\rho }{sin\theta }$,从而这条直线也就由${\rho }_0、{\theta }_0$两参数唯一确定:${\rho }_0=xcos{\theta }_0+ysin{\theta }_0$，这就完成了直线的坐标系变换；而假设存在一个点$(x_0,y_0)$，则经过他的直线必然满足$\rho =x_{0}cos\theta +y_{0}sin\theta$，这就实现了点的坐标系变换。

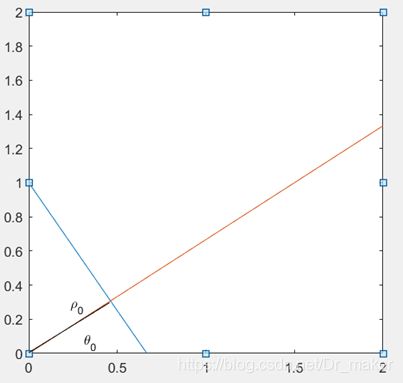
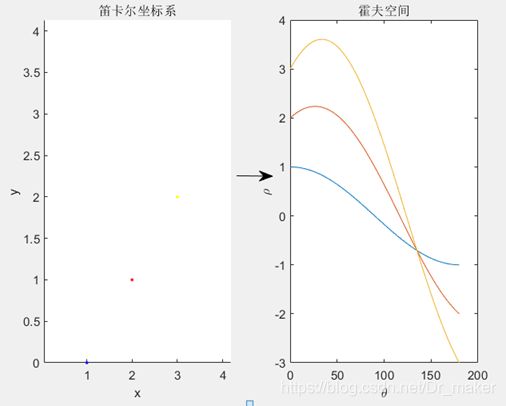
第一张图片给出了直线的霍夫变换过程，第二张图给出了点的霍夫变换，由图二可以看出在同一直线上的三个点映射到霍夫空间上的曲线确实经过了同一点。
霍夫空间中$\theta$的范围为0～180，这是因为原直线斜率的范围就在0～180度范围内变动，给出原直线与x轴正方向夹角$\alpha$、斜率k和$\theta$的对应关系如下:

$\alpha$	k	$\theta$
0	0	90
45	1	135
90	$\infty$	180（0）
135	-1	45
180（0）	0	90

2.算法分析

霍夫直线变换的算法思想分为以下几个步骤：

1. 对图像边缘上的点进行霍夫直线变换。这一步通过构造一个霍夫空间矩阵(或者同样size的一维数组）来实现，它应该可以囊括每个离散的霍夫空间坐标，通常我们会取一个角度最小分辨率${\theta }_0$和距离最小分辨率${\rho }_0$，那么霍夫空间矩阵的大小就应该是$round(\frac{\pi }{{\theta }_0})\times round(2(src.width+src.height)+1)/{\rho }_0)$，角度范围很容易理解就是$\theta$在0～180内变化，距离的范围是因为随着$\theta$的变化，$\rho$的最小值为$-\sqrt{src.widt{h}^2+src.heigh{t}^2}$,最大值为$\sqrt{src.widt{h}^2+src.heigh{t}^2}$，虽然由于角度的限制可能在180范围内可能达不到最小值，但还是给出最稳妥的范围，至于为啥变成了绝对值的形式，估计是因为根号不好运算，用绝对值之和的形式代替了方和根。由此再对边缘图像上每一个点进行霍夫直线边变换，即计算离散的0～180范围内$\theta$对应$\rho$值，矩阵上相应位置计数加一，这样就完成了所有点的变换，记录了它们在霍夫空间上经过的所有点及点的重复次数。
2. 在四邻域范围内进行非极大值抑制与阈值处理。这一步就是遍历霍夫空间矩阵中的每一个点，将该点的重复次数与其十字范围内点的重复次数进行比较同时还需要要阈值比较，如果大于则说明该点对应的很可能是一条直线，将该点存入数组。
3. 对极大值数组从小到大排序。极大值数组中点的重复次数越多，该点对应的越可能是原图中的直线，最终只需输出前LineMax条。
4. 输出直线。由极大值数组返回到霍夫空间矩阵中算出其对应的$\theta 、\rho$，输出直线。

3.使用实例

opencv函数原型：

HoughLines( InputArray image, OutputArray lines,
 double rho, double theta, int threshold,
ouble srn = 0, double stn = 0,
double min_theta = 0, double max_theta = CV_PI );

第一个参数为输入图像，应该为8位单通道边缘图像，即原图经过边缘检测之后的图像；
第二个参数为输出直线，通常二维向量vecto来保存，每一个元素记录了一条直线的$\theta 、\rho$值；
第三个参数为角度分辨率，越小识别出直线越多；
第四个参数为距离分辨率，越小识别出的直线越多；
第五个参数为阈值，即霍夫空间中某点被多少条曲线经过才可认为是直线；
第六、七个参数用于多尺度的霍夫直线检测，取0时就使用普通的霍夫直线检测，多尺度还没涉及，搁置。
第八、九个参数为霍夫空间中$\theta$的取值范围，通常就是取默认值0～180；
实例程序：

int main()
{
	Mat src,gray,dst;
	vector<Vec2f> lines;  //二维向量，接收theta和r
	src = imread("E:\\material\\building.png");
	if (src.empty())
	{
		cout << "未找到该图片";
		return -1;
	}
	Canny(src, gray, 50,200 );
	cvtColor(gray, dst, COLOR_GRAY2BGR);
	HoughLines(gray,lines,1,CV_PI/180,200);  //霍夫直线检测，三参数为扫描像素时的步长，四参数为扫描像素时的角度步长
	//画图
	for(size_t i =0;i<lines.size();i++)
		{
			float rho = lines[i][0], theta = lines[i][1]; //记录直线特征值
			Point p1, p2;
			double a = cos(theta),b = sin(theta);
			double x0 = a * rho, y0 = b * rho;
			p1.x = cvRound(x0 + 1000 * (-b));
			p1.y = cvRound(y0 + 1000 * a);
			p2.x = cvRound(x0 - 1000 * (-b));
			p2.y = cvRound(y0 - 1000 * a);  //因为不知道端点，所以这里取直线长度为1000，以直线和其过原点的法线的交点为原点左右延长
			line(dst, p1, p2, Scalar(55, 100, 195),1,LINE_AA);
		}
	imshow("原图", src);
	imshow("边缘检测后图", gray);
	imshow("霍夫变换后", dst);
	waitKey(0);
}

二、霍夫概率变换

1.数学原理

霍夫概率变化的原理和霍夫直线变换的数学原理是一样的，没有区别，都是将笛卡尔坐标系上的点映射为霍夫空间上的曲线，再根据每个点所被经过的曲线次数多少还原为直线。

2.算法分析

在算法层面上，霍夫概率变换和霍夫直线变换就产生了些许差异，它的基本步骤如下：

1. 记录所有的图像边缘点。
2. 随机选取边缘点构成直线。这一步同样需要构造霍夫空间矩阵，但矩阵构造完毕之后并不是对所有的边缘点进行霍夫变化，而是随机取点进行霍夫变换，同时对变换后的结果进行判断：
   如果不存在某个点的变换结果中存在某一霍夫点$({\theta }_0,{\rho }_0)$被经过的直线数量超过了阈值，则继续随选点进行霍夫变化；
   若存在这样一个或多个霍夫点$({\theta }_0,{\rho }_0)$就选取其中最大一个，认为该点对应一条直线，然后判断该点对应直线的角度（45～135或者是其他两类，为啥这么分也没搞懂），再根据角度的不同给出不同的X,Y方向步进值，向直线的两端不断前进，遇到点是边缘点就认为它也构成了直线，不是则继续前行直到走过了足够多非边缘点（间隔过大）或者遇到图像边界停止。
3. 更新累加器和边缘图像。在第二步得到了一条完整的直线，计算其长度，如果其长度大于阈值就认为它是一条好的直线，对于好的直线要将其上面边缘点对应的所有霍夫空间点计数减一，也就是删掉了这些点对应的霍夫空间曲线，同时不管这条直线是好直线还是非好直线，都要在边缘图像上删去这些点以免重复搜索这些点。（对这里的算法有点疑惑，如果是好直线，一个边缘点同时属于多条直线的话，当它的某一条直线被寻找到，这一点对应曲线在霍夫空间就会消失，那么当我们找到他的另条直线时，其霍夫空间对应点相交曲线数目一定会减少，这会对直线寻找造成影响；即使是非好直线的边缘点，计数器不变化，但由于边缘图像将其除名，在直线推进过程中它会成为间隔的一部分，也可能导致直线的中断，不知道这是怎么解决的）。
4. 输出直线。将好直线的端点保存下来，当收集到的直线数目大于一定值时停止程序。

3.使用实例

opencv源码：

HoughLinesP( InputArray image, OutputArray lines,
double rho, double theta, int threshold,
double minLineLength = 0, double maxLineGap = 0 );

第一个参数为输入图像，应该为8为单通道边缘图；
第二个参数为输出直线数组，通常为具有四个元素的向量vector，保存了直线的端点；
第三个参数为角度分辨率；
第四个参数为距离分辨率；
第五个参数为霍夫空间的阈值，即一个点要被多少曲线经过才认为对应直线；
第六个参数为判断好直线的最小长度；
第七个参数为直线的最小间断距离，即能能容忍的最大间隔；
示例程序：

int main()
{	
	Mat src, gray, dst;
	src = imread("E:\\material\\building.png");
	if (src.empty())
	{
		cout << "not found the picture";
		return -1;
	}
	Canny(src, gray, 100, 200, 3);  //边缘检测
	cvtColor(gray, dst, COLOR_GRAY2BGR);

	vector<Vec4i> lines;  //创建容器容纳向量
	HoughLinesP(gray, lines, 1, CV_PI / 180, 130, 50, 10); //倒数第二个参数为线段最短距离，倒数第一个为当两直线距离小于此值是认为为同一条直线
	for (size_t i = 0;i < lines.size();i++)
	{
		Vec4i l=lines[i];
		line(dst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(142, 54, 231), 1);
	}
	imshow("原图", src);
	imshow("累积概率霍夫变换", dst);
	waitKey(0);
}

参考文献：
霍夫线/圆变换从原理到源码详解
LSD直线检测和霍夫线变换的学习建议
Opencv源代码分析HoughLines
OpenCV3』霍夫变换原理及实现