【推荐算法】从零开始做推荐(三)——传统矩阵分解的TopK推荐实战
前言
在前两章,我们已对本系列的数据集、评价指标做了相应的介绍,从本章开始将进行推荐实战,算法上从最经典的矩阵分解讲起。
目录
- 前言
- 矩阵分解
- 核心算法
- ML100K实现完整的矩阵分解TopK推荐
-
- 构造矩阵
- 训练
- 测试
- 结果分析
- 进阶!灵魂拷问
- 完整代码
如果你对本系列(未写完,持续更新中)感兴趣,可接以下传送门:
【推荐算法】从零开始做推荐(一)——认识推荐、认识数据
【推荐算法】从零开始做推荐(二)——推荐系统的评价指标,计算原理与实现样例
【推荐算法】从零开始做推荐(三)——传统矩阵分解的TopK推荐
【推荐算法】从零开始做推荐(四)——python Keras框架 利用Embedding实现矩阵分解TopK推荐
【推荐算法】从零开始做推荐(五)——贝叶斯个性化排序矩阵分解 (BPRMF) 推荐实战
【推荐算法】从零开始做推荐(六)——贝叶斯性化排序矩阵分解 (BPRMF) 的Tensorflow版
矩阵分解
本系列以实战为主,算法上讲下大概的思想。矩阵分解较全的分析介绍可参照机器学习矩阵分解解析Recommender.Matrix.Factorization。本文实现的是最简的矩阵分解版本,详细思想参照矩阵分解在协同过滤推荐算法中的应用,主体算法公式参照梯度下降的矩阵分解公式推导。
什么是矩阵分解?
下面进行简单介绍。矩阵分解,顾名思义是将矩阵进行拆分,线性代数里两个矩阵相乘可以得到一个新的矩阵,而矩阵分解的思想就是矩阵乘法的逆运用,将一个矩阵分解成两个矩阵相乘。注意,这里的分解是近似的,因为有可能找不出两个矩阵的乘积恰好等于原矩阵。而这个近似就给推荐带来了思路。
分解前的矩阵是什么?
答:用户与项目的交互矩阵,具体含义可以是评分、签到、点击等等。大致分为两类,一类是0-1矩阵,即有过交互即为1,否则为0;另一类是具体的数值,根据交互的次数、评价等得出。这里我们用Rating代指分解前的矩阵。
分解后的两个矩阵分别是什么?
答:分别为用户隐因子矩阵、项目隐因子矩阵,中间维度K认为是特征的数量。这样一来就用两个矩阵分别表示了用户与项目。假设Rating的维度是M×N的,那么就可以分解为M×K的User矩阵,K×N的Item矩阵,满足矩阵Rating和矩阵[User×Item]中的非零项尽可能相等。

为什么要矩阵分解?
答:无论Rating是何种矩阵,我们都默认了如果用户和项目未交互则对应位置填0,但实际上用户对该项目是可能感兴趣的,如何得到这个兴趣程度呢?我们让分解后的矩阵尽量与原矩阵逼近,注意,逼近的只有原矩阵的非零项。因为是近似的分解,所以得到的新矩阵,原先非零位置就有了数值,于是我们就可以根据新矩阵的数值由大到小进行排序取前K个进行TopK推荐。
核心算法
自己写是不可能自己写的,Github上虽然有很多,但都是面向对象的写法。面向对象的代码尽管复用性强,也易于修改,但就是写得太罗嗦,不能很直观的理解。
这里与理论统一,对网上一个广泛流传的版本进行修改,先看理论部分:

修改完的代码如下,采用的是最简单版本的梯度下降,步长alpha和正则lamda(正确打法是lambda,代码写lamda是为了与python中的关键字作区分)固定。
对梯度下降感兴趣的可以重点看下这段代码,关键之处在于梯度下降结束的三个条件:
梯度下降结束条件:
1.满足最大迭代次数;
2.loss过小;
3.loss之差过小,梯度消失。
# -*- coding: utf-8 -*-
"""
Created on Fri Apr 10 14:42:17 2020
@author: Yang Lechuan
"""
import numpy as np
import time
def matrix_factorization(R,P,Q,d,steps,alpha=0.05,lamda=0.002):
Q=Q.T
sum_st = 0 #总时长
e_old = 0 #上一次的loss
flag = 1
for step in range(steps): #梯度下降结束条件:1.满足最大迭代次数,跳出
st = time.time()
e_new = 0
for u in range(len(R)):
for i in range(len(R[u])):
if R[u][i]>0:
eui=R[u][i]-np.dot(P[u,:],Q[:,i])
for k in range(d):
P[u][k] = P[u][k] + alpha*eui * Q[k][i]- lamda *P[u][k]
Q[k][i] = Q[k][i] + alpha*eui * P[u][k]- lamda *Q[k][i]
cnt = 0
for u in range(len(R)):
for i in range(len(R[u])):
if R[u][i]>0:
cnt = cnt + 1
e_new = e_new + pow(R[u][i]-np.dot(P[u,:],Q[:,i]),2)
et = time.time()
e_new = e_new / cnt
if step == 0: #第一次不算loss之差
e_old = e_new
continue
sum_st = sum_st + (et-st)
if e_new<1e-3:#梯度下降结束条件:2.loss过小,跳出
flag = 2
break
if e_old - e_new<1e-10:#梯度下降结束条件:3.loss之差过小,梯度消失,跳出
flag = 3
break
else:
e_old = e_new
print('---------Summary----------\n',
'Type of jump out:',flag,'\n',
'Total steps:',step + 1,'\n',
'Total time:',sum_st,'\n',
'Average time:',sum_st/(step+1.0),'\n',
"The e is:",e_new)
return P,Q.T
R=[
[5,2,0,3,1],
[0,2,1,4,5],
[1,1,0,2,4],
[2,2,0,5,0]
]
d = 3
steps = 5000
N = len(R)
M = len(R[0])
P = np.random.normal(loc=0,scale=0.01,size=(N,d)) #正态分布随机初始化
Q = np.random.normal(loc=0,scale=0.01,size=(M,d))
nP,nQ = matrix_factorization(R,P,Q,d,steps)
print('-----原矩阵R:------')
print(R)
print('-----近似矩阵nR:------')
print(np.dot(nP,nQ.T))
这块代码的目的是为了验证,我们的矩阵分解算法是否真的做到了分解。来看看结果。
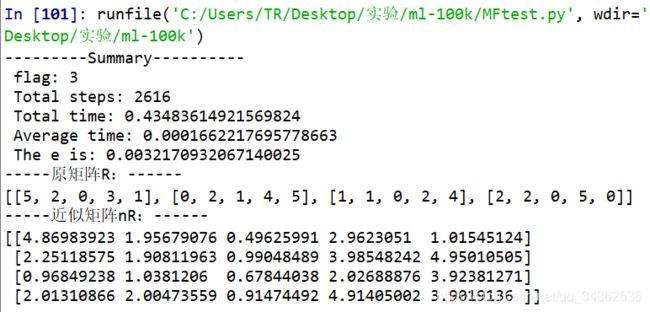
简单来讲,行就是用户,列就是项目,数值可看成评分。可以看出,原先为0的位置也有了评分,我们依靠新矩阵的评分进行推荐。
注意,这里的e是指损失函数,用的是MSE,计算公式如下:
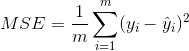
ML100K实现完整的矩阵分解TopK推荐
数据集介绍及训练集测试集划分请看【推荐算法】从零开始做推荐(一)——认识推荐、认识数据
评价指标请看【推荐算法】从零开始做推荐(二)——推荐系统的评价指标,计算原理与实现样例。
简单的数据集介绍:
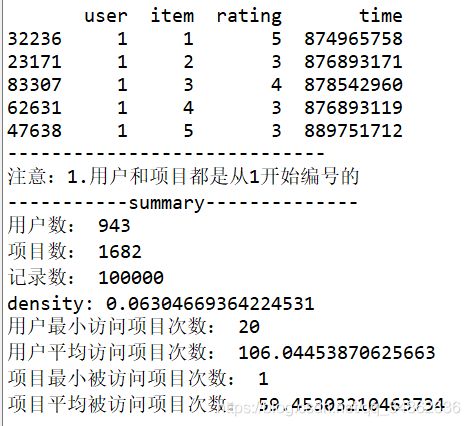
构造矩阵
要将矩阵分解的核心算法进行应用到数据集上,首先要根据数据集得到矩阵R,数据集直接由评分这列,非常简单就可以实现。
def getUI(dsname,dformat): #获取全部用户和项目
st = time.time()
train = pd.read_csv(dsname+'_train.txt',header = None,names = dformat)
test = pd.read_csv(dsname+'_test.txt',header = None,names = dformat)
data = pd.concat([train,test])
all_user = np.unique(data['user'])
all_item = np.unique(data['item'])
train.sort_values(by=['user','item'],axis=0,inplace=True) #先按时间、再按用户排序
num_user = max(all_user)+1
num_item = max(all_item)+1
rating = np.zeros([num_user,num_item])
for i in range(0,len(train)):
user = train.iloc[i]['user']
item = train.iloc[i]['item']
score = train.iloc[i]['rating']
# score = 1
rating[user][item] = score
if os.path.exists('./Basic MF'):
pass
else:
os.mkdir('./Basic MF')
train.to_csv('./Basic MF/train.txt',index = False,header=0)
test.to_csv('./Basic MF/test.txt',index = False,header=0)
np.savetxt('./Basic MF/rating.txt',rating,delimiter=',',newline='\n')
et = time.time()
print("get UI complete! cost time:",et-st)
为了在多次实验里节省时间,我们将构建好的数据存在磁盘中,省得每次都要运行占内存。于是我们还需要一个从本地读数据的函数。
def getData(dformat):
rating = np.loadtxt('./Basic MF/rating.txt',delimiter=',',dtype=float)
train = pd.read_csv('./Basic MF/train.txt',header = None,names = dformat)
test = pd.read_csv('./Basic MF/test.txt',header = None,names = dformat)
data = pd.concat([train,test])
all_user = np.unique(data['user'])
all_item = np.unique(data['item'])
return rating,train,test,all_user,all_item
训练
接下来就可以训练了,训练时包装成函数,方便调用。同样,为了多次实验方便,我们将训练完成的数据存在本地,在测试的时候调用。
def train(rating,d,steps):
R = rating
N=len(R) #用户数
M=len(R[0]) #项目数
P = np.random.normal(loc=0,scale=0.001,size=(N,d))
Q = np.random.normal(loc=0,scale=0.001,size=(M,d))
nP,nQ = matrix_factorization(R,P,Q,d,steps)
# nR=np.dot(nP,nQ.T)
np.savetxt('./Basic MF/nP.txt',nP,delimiter=',',newline='\n')
np.savetxt('./Basic MF/nQ.txt',nQ,delimiter=',',newline='\n')
测试
在测试之前还需要几个步骤,首先是评价指标,这里选用本系列(二)中的PRE,REC,MAP,MRR。代码就不单独展示了,后文有全部代码。
除此之外,我们还需要一个TopK排序的算法。这也是TopK推荐的特色,我们需要返回评分最高的前K个项目,根据评分而得出项目,这里存在评分和项目的对应关系,因此用字典来实现。实现方法就每次找最高的,直到找满K个为止。
def topk(dic,k):
keys = []
values = []
for i in range(0,k):
key,value = max(dic.items(),key=lambda x: x[1])
keys.append(key)
values.append(value)
dic.pop(key)
return keys,values
接下来就是对测试的思考,首先明确,测试的对象是谁?是测试集里的用户! 而非全部用户。
其次,这里提出几点限制:
限制1. 必须推荐给用户其未访问过的项目。 从直觉上来讲,用户访问过的项目用户本身自己知道,如果用户已知一个项目还去交互的话,他带着非常强的主观意愿,此时你推荐或不推荐都不影响他的决策。因此,推荐用户已知的项目,意义是不大的。推荐系统应该更关注用户的深层偏好,通俗来讲就是AI找到你自己都不知道的爱好,给人一种惊喜感。
限制2. 单次推荐中不能给用户重复推荐项目。 这很好理解,实际上这一步是怕用户真实访问记录里有相同的,而TopK推荐只可能推荐一个项目一次,因此若不去重,则评价指标会偏低。
这个限制转化成代码分为三步:
1)去掉测试集中某目标用户已访问过的项目。
2)将测试集中某目标用户的真实访问记录去重。
3)若经过1)2)后测试集中某目标用户的真实访问记录变为空集,则跳过且不计数。
经过上述讨论,我们得到如下代码:
def test(train_data,test_data,all_item,dsname,k):
nP = np.loadtxt('./Basic MF/nP.txt',delimiter=',',dtype=float)
nQ = np.loadtxt('./Basic MF/nQ.txt',delimiter=',',dtype=float)
PRE = 0
REC = 0
MAP = 0
MRR = 0
AP = 0
HITS = 0
sum_R = 0
sum_T = 0
valid_cnt = 0
stime = time.time()
test_user = np.unique(test_data['user'])
for user in test_user:
# user = 0
visited_item = list(train_data[train_data['user']==user]['item'])
# print('访问过的item:',visited_item)
if len(visited_item)==0: #没有训练数据,跳过
continue
per_st = time.time()
testlist = list(test_data[test_data['user']==user]['item'].drop_duplicates()) #去重保留第一个
testlist = list(set(testlist)-set(testlist).intersection(set(visited_item))) #去掉访问过的item
if len(testlist)==0: #过滤后为空,跳过
continue
# print("对用户",user)
valid_cnt = valid_cnt + 1 #有效测试数
poss = {}
for item in all_item:
if item in visited_item:
continue
else:
poss[item] = np.dot(nP[user],nQ[item])
# print(poss)
rankedlist,test_score = topk(poss,k)
# print("Topk推荐:",rankedlist)
# print("实际访问:",testlist)
# print("单条推荐耗时:",time.time() - per_st)
AP_i,len_R,len_T,MRR_i,HITS_i= cal_indicators(rankedlist, testlist)
AP += AP_i
sum_R += len_R
sum_T += len_T
MRR += MRR_i
HITS += HITS_i
# print(test_score)
# print('--------')
# break
etime = time.time()
PRE = HITS/(sum_R*1.0)
REC = HITS/(sum_T*1.0)
MAP = AP/(valid_cnt*1.0)
MRR = MRR/(valid_cnt*1.0)
p_time = (etime-stime)/valid_cnt
print('评价指标如下:')
print('PRE@',k,':',PRE)
print('REC@',k,':',REC)
print('MAP@',k,':',MAP)
print('MRR@',k,':',MRR)
print('平均每条推荐耗时:',p_time)
with open('./Basic MF/result_'+dsname+'.txt','w') as f:
f.write('评价指标如下:\n')
f.write('PRE@'+str(k)+':'+str(PRE)+'\n')
f.write('REC@'+str(k)+':'+str(REC)+'\n')
f.write('MAP@'+str(k)+':'+str(MAP)+'\n')
f.write('MRR@'+str(k)+':'+str(MRR)+'\n')
f.write('平均每条推荐耗时@:'+str(k)+':'+str(p_time)+'\n')
结果分析
这里的迭代次数就不像自己构造的小矩阵那样设那么高了,因为时间成本比较高,且也并非迭代越多越好。
这里摆一个多次运行TopK@10的结果,注意这里的 d = 40 , α = 0.05 , λ = 0.002 d=40,α=0.05,λ=0.002 d=40,α=0.05,λ=0.002,别问,问就是试出来的。可以看出随step的迭代次数,指标先增后减。
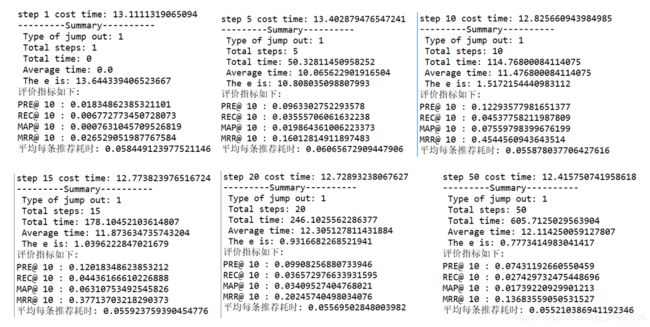
进阶!灵魂拷问
拷问1. 矩阵分解的效果与什么因素有关?
1) 与潜在因子矩阵P,Q的初始值有关。一开始看网上说直接(0,1)之间,但实际效果很差,后来调小了才变好,猜测是过大的话如果跑偏了(即本来不喜欢结果初值很高),梯度一直下降也救不回来,还有就是正态分布可以有负数,这在潜在特征里是允许的,而(0,1)要变为负数更加困难,都是正数变相地增加了分解地难度。
2) 与学习率α与正则参数λ有关。这个有两种解决方式,欧皇之间随便调,玄学调参。老实人可以选择更好的梯度下降策略,SGD,ADAM等等。
3) 与潜在矩阵的维度d有关。这个可以有限范围内的调试,如20~100,20一增。如果是打比赛的话还是看脸。
3) 与迭代次数steps有关。欧皇笑了,非酋哭了。
拷问2. 为什么steps越高,效果有可能反而不好?
在本实验中,steps越高,损失e确实是在下降,但效果反而不好,用机器学习的理论来讲,这就是出现了过拟合。其次,如果是0-1矩阵,从主观上来分析,交互过和喜欢并非是绝对关系,因此越贴合原矩阵,并非就越喜欢。
拷问3. 评分矩阵和0-1矩阵,哪个效果好?
这个应该没有绝对的比较,从本次实验来讲,下图为0-1矩阵分解的结果,是评分的更好。理论上看似如果评分信息是真是代表用户偏好,那么评分的会更好,实则用户的偏好是在一直变化的,0-1矩阵更提供了泛化的可能,而评分限制的较死。更真实的情况在于用户评分数据会过于稀疏,真实环境里很难有效,而0-1交互数据更容易收集,也就更稠密。因此我个人是站0-1这边的。

拷问4. 换个大点的数据集(ML1M),效果怎么样?
下图为参数不动,直接拿来用的结果。

1)参数需要重新调整。
2)时间开销猛增,传统矩阵分解本身就是一个时间开销较大的算法,这与矩阵的构建方式、行列数量有关。
PS:求点赞、关注、打赏,毕竟这些我都没啥-。-
完整代码
# -*- coding: utf-8 -*-
"""
Created on Sat Oct 19 12:37:04 2019
@author: YLC
"""
import os
import numpy as np
import pandas as pd
import time
import math
def getUI(dsname,dformat): #获取全部用户和项目
st = time.time()
train = pd.read_csv(dsname+'_train.txt',header = None,names = dformat)
test = pd.read_csv(dsname+'_test.txt',header = None,names = dformat)
data = pd.concat([train,test])
all_user = np.unique(data['user'])
all_item = np.unique(data['item'])
train.sort_values(by=['user','item'],axis=0,inplace=True) #先按时间、再按用户排序
num_user = max(all_user)+1
num_item = max(all_item)+1
rating = np.zeros([num_user,num_item])
for i in range(0,len(train)):
user = train.iloc[i]['user']
item = train.iloc[i]['item']
score = train.iloc[i]['rating']
# score = 1
rating[user][item] = score
if os.path.exists('./Basic MF'):
pass
else:
os.mkdir('./Basic MF')
train.to_csv('./Basic MF/train.txt',index = False,header=0)
test.to_csv('./Basic MF/test.txt',index = False,header=0)
np.savetxt('./Basic MF/rating.txt',rating,delimiter=',',newline='\n')
et = time.time()
print("get UI complete! cost time:",et-st)
def getData(dformat):
rating = np.loadtxt('./Basic MF/rating.txt',delimiter=',',dtype=float)
train = pd.read_csv('./Basic MF/train.txt',header = None,names = dformat)
test = pd.read_csv('./Basic MF/test.txt',header = None,names = dformat)
data = pd.concat([train,test])
all_user = np.unique(data['user'])
all_item = np.unique(data['item'])
return rating,train,test,all_user,all_item
def topk(dic,k):
keys = []
values = []
for i in range(0,k):
key,value = max(dic.items(),key=lambda x: x[1])
keys.append(key)
values.append(value)
dic.pop(key)
return keys,values
def cal_indicators(rankedlist, testlist):
HITS_i = 0
sum_precs = 0
AP_i = 0
len_R = 0
len_T = 0
MRR_i = 0
ranked_score = []
for n in range(len(rankedlist)):
if rankedlist[n] in testlist:
HITS_i += 1
sum_precs += HITS_i / (n + 1.0)
if MRR_i == 0:
MRR_i = 1.0/(rankedlist.index(rankedlist[n])+1)
else:
ranked_score.append(0)
if HITS_i > 0:
AP_i = sum_precs/len(testlist)
len_R = len(rankedlist)
len_T = len(testlist)
return AP_i,len_R,len_T,MRR_i,HITS_i
def matrix_factorization(R,P,Q,d,steps,alpha=0.002,lamda=2e-6):
Q=Q.T
sum_st = 0 #总时长
e_old = 0 #上一次的loss
flag = 1
for step in range(steps): #梯度下降结束条件:1.满足最大迭代次数,跳出
st = time.time()
e_new = 0
for u in range(len(R)):
for i in range(len(R[u])):
if R[u][i]>0:
eui=R[u][i]-np.dot(P[u,:],Q[:,i])
for k in range(d):
P[u][k] = P[u][k] + alpha*eui * Q[k][i]- lamda *P[u][k]
Q[k][i] = Q[k][i] + alpha*eui * P[u][k]- lamda *Q[k][i]
cnt = 0
for u in range(len(R)):
for i in range(len(R[u])):
if R[u][i]>0:
cnt = cnt + 1
e_new = e_new + pow(R[u][i]-np.dot(P[u,:],Q[:,i]),2)
et = time.time()
print('step',step+1,'cost time:',et-st)
e_new = e_new / cnt
if step == 0: #第一次不算loss之差
e_old = e_new
continue
sum_st = sum_st + (et-st)
if e_new<1e-3:#梯度下降结束条件:2.loss过小,跳出
flag = 2
break
if e_old - e_new<1e-10:#梯度下降结束条件:3.loss之差过小,梯度消失,跳出
flag = 3
break
else:
e_old = e_new
print('---------Summary----------\n',
'Type of jump out:',flag,'\n',
'Total steps:',step + 1,'\n',
'Total time:',sum_st,'\n',
'Average time:',sum_st/(step+1.0),'\n',
"The e is:",e_new)
return P,Q.T
def train(rating,d,steps):
R = rating
N=len(R) #用户数
M=len(R[0]) #项目数
P = np.random.normal(loc=0,scale=0.01,size=(N,d))
Q = np.random.normal(loc=0,scale=0.01,size=(M,d))
nP,nQ = matrix_factorization(R,P,Q,d,steps)
# nR=np.dot(nP,nQ.T)
np.savetxt('./Basic MF/nP.txt',nP,delimiter=',',newline='\n')
np.savetxt('./Basic MF/nQ.txt',nQ,delimiter=',',newline='\n')
def test(train_data,test_data,all_item,dsname,k):
nP = np.loadtxt('./Basic MF/nP.txt',delimiter=',',dtype=float)
nQ = np.loadtxt('./Basic MF/nQ.txt',delimiter=',',dtype=float)
PRE = 0
REC = 0
MAP = 0
MRR = 0
AP = 0
HITS = 0
sum_R = 0
sum_T = 0
valid_cnt = 0
stime = time.time()
test_user = np.unique(test_data['user'])
for user in test_user:
# user = 0
visited_item = list(train_data[train_data['user']==user]['item'])
# print('访问过的item:',visited_item)
if len(visited_item)==0: #没有训练数据,跳过
continue
per_st = time.time()
testlist = list(test_data[test_data['user']==user]['item'].drop_duplicates()) #去重保留第一个
testlist = list(set(testlist)-set(testlist).intersection(set(visited_item))) #去掉访问过的item
if len(testlist)==0: #过滤后为空,跳过
continue
# print("对用户",user)
valid_cnt = valid_cnt + 1 #有效测试数
poss = {}
for item in all_item:
if item in visited_item:
continue
else:
poss[item] = np.dot(nP[user],nQ[item])
# print(poss)
rankedlist,test_score = topk(poss,k)
# print("Topk推荐:",rankedlist)
# print("实际访问:",testlist)
# print("单条推荐耗时:",time.time() - per_st)
AP_i,len_R,len_T,MRR_i,HITS_i= cal_indicators(rankedlist, testlist)
AP += AP_i
sum_R += len_R
sum_T += len_T
MRR += MRR_i
HITS += HITS_i
# print(test_score)
# print('--------')
# break
etime = time.time()
PRE = HITS/(sum_R*1.0)
REC = HITS/(sum_T*1.0)
MAP = AP/(valid_cnt*1.0)
MRR = MRR/(valid_cnt*1.0)
p_time = (etime-stime)/valid_cnt
print('评价指标如下:')
print('PRE@',k,':',PRE)
print('REC@',k,':',REC)
print('MAP@',k,':',MAP)
print('MRR@',k,':',MRR)
print('平均每条推荐耗时:',p_time)
with open('./Basic MF/result_'+dsname+'.txt','w') as f:
f.write('评价指标如下:\n')
f.write('PRE@'+str(k)+':'+str(PRE)+'\n')
f.write('REC@'+str(k)+':'+str(REC)+'\n')
f.write('MAP@'+str(k)+':'+str(MAP)+'\n')
f.write('MRR@'+str(k)+':'+str(MRR)+'\n')
f.write('平均每条推荐耗时@:'+str(k)+':'+str(p_time)+'\n')
if __name__ == '__main__':
dsname = 'ML100K'
dformat = ['user','item','rating','time']
getUI(dsname,dformat) #第一次使用后可注释
rating,train_data,test_data,all_user,all_item = getData(dformat)
d = 40 #隐因子维度
steps = 10
k = 10
train(rating,d,steps)
test(train_data,test_data,all_item,dsname,k)