PyTorch入门到进阶实战笔记一（慕课网）

PyTorch入门基础串讲

PyTorch的基本概念

Tensor

有时遇到的数据是很高维度的，很难使用矩阵或向量来描述，这时就用张量来描述任意维度的物体

Variable（autograd）

用变量来表达参数

nn.Module

封装了许多神经网络结构

Tensor与机器学习的关系

我们使用tensor来对样本和模型进行描述

Tensor的类型

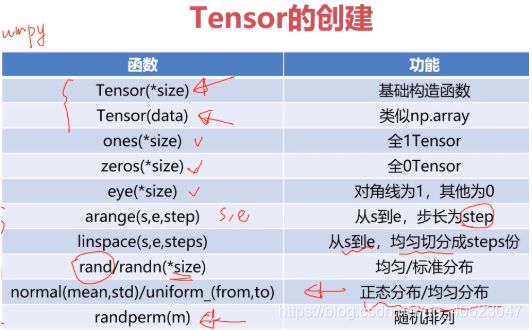
Tensor的创建

Tensor创建编程实例

import torch
'''
几种特殊的tensor
'''
a = torch.Tensor([[1,2],[3,4]])
print(a)
print(a.type())

b = torch.Tensor(2,3) #定义一个2×3的二阶tensor
#使用shape来定义时，初始值为随机值
print(b)
print(b.type())

c = torch.ones(2,2)
print(c)
print(c.type())

d = torch.eye(2,2)
print(d)
print(d.type())

e = torch.zeros(2,2)
print(e)
print(e.type())

f = torch.zeros_like(b) #跟某个tensor相同shape的全0tensor
f = torch.ones_like(b)
print(f)
print(f.type())
print("+++++++++++++++++++++++++++++++++++++++++")
'''
随机
'''
a = torch.rand(2,2)
#随机生成某个shape的tensor
print(a)
print(a.type())

b = torch.normal(mean = 0.0, std = torch.rand(5))
#构造5组不同的高斯正态分布
#生成随机满足正态分布的值
print(b)
print(b.type())

c = torch.normal(mean = torch.rand(5), std = torch.rand(5))
#随机五组均值和标准差
print(c)
print(c.type())

d = torch.Tensor(2,2).uniform_(-1,1)
#定义均匀分布
#需要先指定tensor的大小，然后再定义(-1,1)之间的均匀分布
print(d)
print(d.type())

print("+++++++++++++++++++++++++++++++++++++++++")
'''
序列
'''
a = torch.arange(0,10,2)
#定义[0,10)中步长为2的序列
print(a)
print(a.type())

b = torch.linspace(2,10,3)#拿到等间隔的n个数字
#定义一个在[2,10]之间的3个数字的等间隔序列
print(b)
print(b.type())

c = torch.randperm(10)
#生成一个[0,10)的打乱序列
print(c)
print(c.type())

print("+++++++++++++++++++++++++++++++++++++++++")
###############对比
import numpy as np

a = np.array([[1,2],[3,4]])
print(a)

tensor与numpy很相似，就像是在numpy外面套了一层tensor

Tensor的属性

每一个Tensor有torch.dtype、torch.device、torch.layout三种属性

torch.device标识了torch.Tensor对象在创建之后所存储在的设备名称（CPU/GPU(Cuda 0 1 2)）

torch.layout表示torch.Tensor内存布局的对象（稠密的张量）【sparse张量以稀疏形式进行存储】

torch.tensor([1,2,3],dtype=torch.float32,device=torch.device('cpu')) 
#定义稠密的张量

稀疏的张量

稀疏：描述了当前的数据中非零元素的个数

• torch.sparse_coo_tensor
• coo类型表示了非零元素的坐标形式

indices = torch.tensor([[0,1,1],[2,0,2]]) # 非零元素的坐标值
values = torch.tensor([3,4,5],dtype=torch.float32)# 非零元素的值
x = torch.sparse_coo_tensor(indices,values,[2,4])#shape=2×4

import torch
dev = torch.device("cpu")#将tensor放置在cpu上计算
#dev = torch.device("cuda:0") #放置在第0块显卡上
a = torch.tensor([2,2],dtype=torch.float32,device = dev)
print(a)

#定义稀疏张量
i = torch.tensor([[0,1,2],[0,1,2]])
v = torch.tensor([1,2,3])
a = torch.sparse_coo_tensor(i,v,(4,4))
print(a)
a = torch.sparse_coo_tensor(i,v,(4,4)).to_dense()#转成稠密张量
print(a)
a = torch.sparse_coo_tensor(i,v,(4,4),dtype = torch.float32,device = dev)
print(a)

Tensor的算术运算

加法运算

c = a + b
c = torch.add(a,b)
a.add(b)
#带下划线的方式在计算的同时将a的值进行修改
a.add_(b)

减法运算

c = a - b
c = torch.sub(a,b)
a.sub(b)
a.sub_(b)

乘法运算

哈达玛积（element wise，对应元素相乘【维度相同】）

c = a * b
c = torch.mul(a,b)
a.mul(b)
a.mul_(b)

除法运算

c = a / b
c = torch.div(a,b)
a.div(b)
a.div_(b)

矩阵运算

二维矩阵乘法运算操作包括torch.mm()、torch.matmul()、@

矩阵维度首尾呼应

a = torch.ones(2,1)
b = torch.ones(1,2)
print(torch.mm(a,b))
print(torch.matmul(a,b))
print(a @ b)
print(a.matmul(b))
print(a.mm(b))

• 对于高维的Tensor（dim>2），定义其矩阵乘法仅在最后的两个维度，要求前面的维度必须保持一致，就像矩阵的索引一样并且运算操作只有torch.matmul()

a = torch.ones(1,2,3,4)
b = torch.ones(1,2,4,3)
print(a.matmul(b))
print(torch.matmul(a,b))

幂运算

print(torch.pow(a,2))
print(a.pow(2))
print(a**2)
print(a.pow_(2))

$e^n$

print(torch.exp(a))
b = a.exp_()

开方运算

print(a.sqrt())
print(a.sqrt_())

对数运算

print(torch.log2(a))
print(torch.log10(a))
#底数为e
print(torch.log(a))
print(torch.log_(a))

in-place的概念和广播机制

in-place操作

in-place操作是指：计算中不允许使用临时变量，“就地”操作

也称为原位操作

• x = x + y

• add_、sub_、mul_等等

广播机制

广播机制：运算中，张量参数可以自动扩展为相同大小

广播机制需要满足两个条件：

• 每个张量至少有一个维度
• 满足右对齐（张量维度以右边补满）【从右往左看两个张量的对应值有1或者相等即为满足右对齐】
• torch.rand(2,1,1)+torch.rand(3)

#广播机制
import torch

a = torch.rand(2,3)
b = torch.rand(3)
# a , 2 * 3
# b , 1 * 3
# c , 2 * 3
c = a + b

print(a)
print(b)
print(c)
print(c.shape)

a = torch.rand(2,3)
b = torch.rand(2)
# a , 2 * 3
# b , 1 * 2
#无法进行广播，报错
c = a + b
print(a)
print(b)
print(c)
print(c.shape)

a = torch.rand(2,1)
b = torch.rand(2)
# a , 2 * 1
# b , 1 * 2
# c , 2 * 2
c = a + b
print(a)
print(b)
print(c)
print(c.shape)

a = torch.rand(2,1,1,3)
b = torch.rand(4,2,3)
# a , 2 * 1 * 1 * 3
# b , 1 * 4 * 2 * 3
# c , 2 * 4 * 2 * 3
c = a + b
print(a)
print(b)
print(c)
print(c.shape)

Tensor的取整/取余运算

• .floor()向下取整数
• .ceil()向下取整
• .round()四舍五入 >=0.5向上取整 ，<=0.5向下取整
• .trunc()裁剪，只取整数部分
• .frac()只取小数部分
• %取余

Tensor的比较运算/排序

除了equal其他返回仍为tensor

sort()排序：维度，对于二维数据：dim=0 按列排序，dim=1 按行排序，默认 dim=1

Tensor的三角函数

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AmV0zocQ-1616415672825)(https://gitee.com/Lluvia233/cloudimages/raw/master/img/image-20210320171221787.png)]

Tensor中其他的数学函数

torch.sign()

符号函数，可以类比为分段函数

可以用于分类

Tensor中统计学相关的函数

import torch

a = torch.rand(2,2)

print(a)
print(torch.mean(a))
print(torch.mean(a,dim=0)) #对每一列求均值
print(torch.sum(a))
print(torch.prod(a))

print(torch.argmax(a,dim=0))
print(torch.argmin(a))

print(torch.std(a))
print(torch.var(a))

print(torch.median(a))
print(torch.mode(a))

#########
print("#################")
a = torch.rand(2,2) * 10 #使随机值不在01之间
print(a)
print(torch.histc(a,6,0,0))

a = torch.randint(0,10,[10])
print(torch.bincount(a)) #统计出现的频次，只能用来处理一维tensor

Tensor的torch.distributions

distributions包含可参数化的概率分布和采样函数

• 得分函数
  • 强化学习中策略梯度方法的基础
• pathwise derivative估计器
  • 变分自动编码器中重新参数化技巧

涉及到的分布：

对两个分布相似性的度量：KL Divergence

两个分布的转换：Transforms

对分布的约束：Constraint

Tensor中的随机抽样

1. 定义随机种子

   • torch.manual_seed(seed)

   当定义随机种子后，生成的分布的效果：

   通过定义随机种子，保证随机抽样的结果相同

2. 定义随机数满足的分布

   • torch.normal()

import torch

torch.manual_seed(1)

mean = torch.rand(1,2)
std = torch.rand(1,2)
print(torch.normal(mean,std))

Tensor中的范数运算

范数

• 在泛函分析中，它定义在赋范线性空间中，并满足一定的条件：1.非负性；2.齐次性；3.三角不等式。
• 常被用来度量某个向量空间（或矩阵）中的每个向量的长度或大小（模）

0范数/1范数/2范数/p范数/核范数(用于低秩问题的求解）

• torch.dist(input,other,p=2) 计算p范数
• torch.norm() 计算2范数【针对向量或矩阵】

import torch

a = torch.rand(2,3)
b = torch.rand(2,3)

print(a,b)
print(torch.dist(a,b,p = 1)) #l1: |a-b|
print(torch.dist(a,b,p = 2)) #l2: sqrt((a-b)^{2})
print(torch.dist(a,b,p = 3)) #l3: sqrt((a-b)^{3})
print("#########")
print(torch.norm(a))
print(torch.norm(a,p = 3))
print(torch.norm(a,p="fro")) #核范数

Tensor中的矩阵分解

常见的矩阵分解：

• LU分解：将矩阵A分解成L（下三角）矩阵和U（上三角）矩阵的乘积
• QR分解：将原矩阵分解成一个正交矩阵Q和一个上三角矩阵R的乘积
• EVD分解：特征值分解 【----> PCA】
• SVD分解：奇异值分解 【-----> LDA(引入学习因素，有监督算法)】

特征值分解

• 将矩阵分解为由其特征值和特征向量表示的矩阵之积的方法
• 特征值 VS 特征向量

需要保证输入矩阵为一个方阵

PCA与特征值分解

PCA是特征值分解的重要应用

• PCA：将n维特征映射到k维上，这k维是全新的正交特征，也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征
• PCA算法的优化目标就是：
  • 降维后同一维度的方差最大（特征越丰富）
  • 不同维度之间的相关性为0（冗余低）
  • 协方差矩阵

奇异值分解

如果当前输入矩阵不是方阵，使用奇异值分解

$\sum$是一个特征向量，$U和V$是左奇异矩阵和右奇异矩阵

特征值分解是奇异值分解SVD的一个特例，当左奇异矩阵 = 右奇异矩阵时，就变成了特征值分解EVD

LDA与奇异值分解

LDA算法的核心思想：同类样本之间距离尽可能小；不同类样本之间距离尽可能大

如何通过数学形式表示“距离”？

使用代价函数：$J(w)=\frac{w^T{S}_{B}w}{w^T{S}_{W}w}$

$S_B$不同类物体间距离（协方差矩阵）

$S_W$同类物体间间隔

$S_W^{-1}{S}_{B}w=\lambda w$

• EVD分解 VS SVD分解（要求）
  • 矩阵方阵且满秩（可对角化）【EVD】
  • 矩阵分解不等于特征降维度
  • 协方差矩阵描述方差和相关性
• Pytorch中的奇异值分解
  • torch.svd()

Tensor的裁剪运算

import torch

#裁剪
a = torch.rand(2,2) * 10
print(a)

a = a.clamp(1,2)
print(a)

#tensor([[1.6576, 4.8902],
#        [8.8829, 7.2525]])
#tensor([[1.6576, 2.0000],
#        [2.0000, 2.0000]])

a = a.clamp(2,5)
print(a)
#tensor([[9.4678, 1.8242],
#        [2.5214, 0.8120]])
#tensor([[5.0000, 2.0000],
#        [2.5214, 2.0000]])

Tensor的索引和数据筛选

torch.gather()是按照值来聚合的（Index tensor must have the same number of dimensions as input tensor）

torch.index_select()是按照维度来聚合的

import torch
#tensor的数据筛选
#torch.where
a = torch.rand(4,4)
b = torch.rand(4,4)
print(a)
print(b)

out = torch.where(a > 0.5,a,b) #如果a中的值>0.5就选择a；否则选择b
print(out)

#torch.index_select()
print("##########index_select#########")
a = torch.rand(4,4)
print(a)
out = torch.index_select(a,dim=0,index =torch.tensor([0,3,2])) #选择第0,3,2行数据
print(out,out.shape)

#torch.gather
print("#################gather###################")
a = torch.linspace(1,16,16).view(4,4)
print(a)
out = torch.gather(a,dim = 0,index = torch.tensor([[0,1,1,1],
                                            [0,1,2,2],
                                            [0,1,3,3]]))
print(out)
#tensor([[ 1.,  2.,  3.,  4.],
#        [ 5.,  6.,  7.,  8.],
#        [ 9., 10., 11., 12.],
#        [13., 14., 15., 16.]])
#tensor([[ 1.,  6.,  7.,  8.],
#        [ 1.,  6., 11., 12.],
#        [ 1.,  6., 15., 16.]])

#torch.masked_index
print("#################masked_select#################")
a = torch.linspace(1,16,16).view(4,4)
mask = torch.gt(a,8)
print(a)
print(mask)
out = torch.masked_select(a,mask)
print(out)
#tensor([ 9., 10., 11., 12., 13., 14., 15., 16.])


#torch.take
print("################take################")
a = torch.linspace(1,16,16).view(4,4)
print(a)
b = torch.take(a,index = torch.tensor([0,15,13,10]))
print(b)
#tensor([ 1., 16., 14., 11.])


#torch.nonzero
print("################nonzero#################")
a = torch.tensor([[0,1,2,0],[2,3,0,1]])
print(a)
out = torch.nonzero(a)
print(out)
#tensor([[0, 1],
#        [0, 2],
#        [1, 0],
#        [1, 1],
#        [1, 3]])

Tensor的组合/拼接

torch.cat()拼接后维度仍为原tensor维度

tensor.stack拼接后维度可以发生变化

import torch

## 组合拼接
## torch.cat
a = torch.zeros((2,4))
b = torch.ones((2,4))

out = torch.cat((a,b),dim=0) # 行拼接
print(out)

out = torch.cat((a,b),dim=1) # 列拼接
print(out)

## torch.stack
print("################stack####################")
a = torch.linspace(1,6,6).view(2,3)
b = torch.linspace(7,12,6).view(2,3)
print(a,b)
out = torch.stack((a,b),dim=0)
print(out)
print(out.shape)

#tensor([[1., 2., 3.],
#        [4., 5., 6.]]) tensor([[ 7.,  8.,  9.],
#        [10., 11., 12.]])
#tensor([[[ 1.,  2.,  3.],
#         [ 4.,  5.,  6.]],
#
#        [[ 7.,  8.,  9.],
#         [10., 11., 12.]]])
#torch.Size([2, 2, 3])

out = torch.stack((a,b),dim=1)
print(out)
print(out.shape)
#tensor([[[ 1.,  2.,  3.],
#         [ 7.,  8.,  9.]],
#
#        [[ 4.,  5.,  6.],
#         [10., 11., 12.]]])
torch.Size([2, 2, 3])
out = torch.stack((a,b),dim=2)
print(out)
print(out.shape)
#tensor([[[ 1.,  7.],
#         [ 2.,  8.],
#         [ 3.,  9.]],

#        [[ 4., 10.],
 #        [ 5., 11.],
#         [ 6., 12.]]])
#torch.Size([2, 3, 2])

Tensor的切片

import torch

## 切片
a = torch.rand((3,4))
print(a)
out = torch.chunk(a,2,dim=0)
print(out[0],out[0].shape)
print(out[1],out[1].shape)
#tensor([[0.0994, 0.5468, 0.4318, 0.1000],
#        [0.6685, 0.7013, 0.1311, 0.7307]]) torch.Size([2, 4])
#tensor([[0.9337, 0.4569, 0.9381, 0.0411]]) torch.Size([1, 4])

out = torch.chunk(a,2,dim=1)
print(out[0],out[0].shape)
print(out[1],out[1].shape)
#tensor([[0.4611, 0.5054],
#        [0.0859, 0.1262],
#        [0.5860, 0.9879]]) torch.Size([3, 2])
#tensor([[0.1935, 0.7539],
#        [0.7411, 0.7511],
#        [0.9148, 0.5370]]) torch.Size([3, 2])

##split
print("######################split#####################")
out = torch.split(a,2,dim=1)
print(out)

out = torch.split(a,3,dim=0)
print(out)

a = torch.rand(10,4)
print(a)
out = torch.split(a,3,dim=0)
print(len(out))
for t in out:
    print(t,t.shape)

out = torch.split(a,[1,3,6],dim=0)
print(len(out))
for t in out:
    print(t,t.shape)

Tensor的变形操作

k为负数->顺时针

k为正数->逆时针

有几个k就旋转几个90°

import torch

##张量变形
a = torch.rand(2,3)
print(a)
out = torch.reshape(a,(3,2))
print(out)
print(torch.t(out))

print(torch.transpose(out,0,1))

print("******************")
a = torch.rand(1,2,3)
print("a= ",a)
out = torch.transpose(a,0,1) # 交换两个维度
print(out)
print(out.shape)

out = torch.squeeze(a) #去除维度大小为1的
print(out)

out = torch.unsqueeze(a,-1) #在指定位置添加维度
print(out.shape)

out = torch.unbind(a,dim=2) #去除某个维度
print(out)

print('a= ',a)
print(torch.flip(a,dims=[1])) #反转维度

print("a= ",a)
out = torch.rot90(a)
print(out)
print(out.shape)

Tensor的填充操作

定义Tensor，并填充指定的数值

• torch.full((2,3),3.14)
  • print:tensor([[3.14,3.14,3.14],[3.14,3.14,3.14]])

Tensor的频谱操作

（用在傅里叶变换）

Pytorch简单编程技巧

模型的保存/加载

• torch.saves(state,dir) 保存/序列化

• torch.load(dir) 加载模型

并行化

• torch.get_num_threads(): 获得用于并行化CPU操作的OpenMP线程数
• torch.set_num_threads(int): 设定用于并行化CPU操作的OpenMP线程数

分布式

• python在默认情况下只使用一个GPU，在多个GPU的情况下就需要使用pytorch提供的DataParallel
• 单机多卡
• 多机多卡

Tensor on GPU

• 用方法to()可以将Tensor在CPU和GPU（需要硬件支持）之间相互移动
• 如下示例代码：

一般在处理数据时放在CPU上，处理模型时放在GPU上

Tensor的相关配置

Tensor与numpy的相互转换

torch.from_numpy(ndarry) 将numpy转为tensor

a.numpy() 将tensor转化为numpy

Variable & Autograd

什么是导数？

• 导数（一元函数）是变化率、是切线的斜率、是瞬时速度

什么是方向导数？

• 函数在A点无数个切线的斜率的定义。每一个切线都代表一个变化的方向

什么是偏导数？

• 多元函数降维时候的变化，比如：二元函数固定y,只让x单独变化，从而看成是关于x的一元函数的变化来研究

什么是梯度

函数在A点无数个变化方向中变化最快的那个方向。

记为：$\nabla f$ 或者$gradf=(\frac{\partial \phi }{\partial x},\frac{\partial \phi }{\partial y},\frac{\partial \phi }{\partial z})$

（$x,y,z$分别为下降的三个方向）

梯度与机器学习中的最优解

使用监督学习为例：

代价函数的图像类似：

我们需要不停地沿着梯度下降，来寻找最低点

Variable is Tensor

目前Variable已经与Tensor合并。

每个tensor通过requires_grad来设置是否计算梯度（默认为false）

• 用来冻结某些层的参数

如何计算梯度

关于Autograd的几个概念（自动计算梯度）

只有叶子张量（leaf）才有梯度值，如图x有梯度值，y的梯度值为None

每次计算backward时，需要将前一时刻的梯度归零，否则梯度会一直累加。

backward函数

grad函数

torch.autograd包中的其他函数

function

import torch

class line(torch.autograd.Function):
    @staticmethod
    def forward(ctx,w,x,b):
        #y = w*x +b
        ctx.save_for_backward(w,x,b)
        return w * x + b

    @staticmethod
    def backward(ctx,grad_out):
        w,x,b = ctx.saved_tensors
        
        grad_w = grad_out * x
        grad_x = grad_out * w
        grad_b = grad_out
        
        return grad_w,grad_x,grad_b

w = torch.rand(2,2,requires_grad = True)
x = torch.rand(2,2,requires_grad = True)
b = torch.rand(2,2,requires_grad = True)

out = line.apply(w,x,b)
out.backward(torch.ones(2,2))

print(w,x,b)
print(w.grad,x.grad,b.grad)

torch.nn库

nn.Parameter

nn.Linear & nn.conv2d && nn.ReLU & nn.MaxPool2d(2) & nn.MSELoss 等等

nn.functional

如果有学习参数的话，经常使用nn.Xxx

nn.Sequential

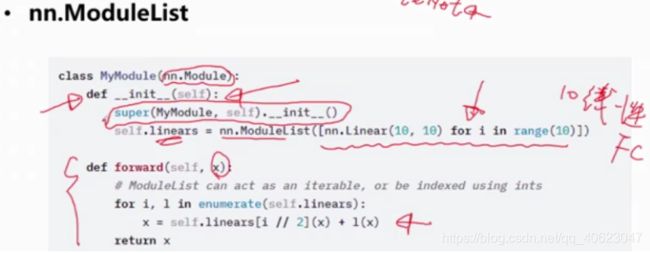
nn.ModuleList

nn.ModuleDict

nn.Module

在model.parameters()中获取可训练的参数

在model.buffers()中获取不可训练的参数

在model.state_dict()访问当前网络结构中的所有参数

Parameters VS buffers

state_dict() & load_state_dict

visdom

类似于一个库

结果展示：

tensorboardX

Pytorch数据可视化工具

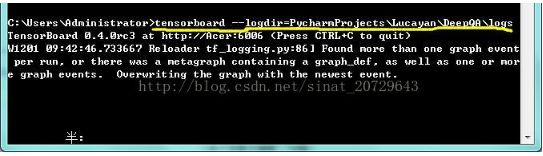
在pytorch中使用tensorboardX的方法：

安装：使用conda 安装，打开anacond powershell，输入pip install tensorboard ，然后安装pip install tensorflow

使用：在程序开头加入

from torch.utils.tensorboard import SummaryWriter

例如下图在jupyter中执行一次得到的文件

在该目录前的上级目录框内cmd，输入

tensorboard --logdir=地址

之后复制路径在Chrome中运行

torchvision

一个图形处理的库