李宏毅老师2022机器学习课程笔记 01 Introduction of Deep Learning
01 Introduction of Deep Learning
机器学习相关规定
什么是机器学习
机器学习的概念
我觉得李老师讲得非常好的一点就是,他真正说清楚了机器学习中的一些因果逻辑。
比如我之前在网络上查阅过一些资料,他们在介绍机器学习时,很多时候上来就说机器学习“是机器学习过去的经验”、“模仿人类学习”等等,但是看了这些解释之后对机器学习是什么还是没有一个清晰的概念。按照我个人对李老师课程的理解,这个的因果关系是有些问题的,可能在最初设计这些模型的时候,学者门只是从数学的角度,探索一种解决问题的方法,然后最后发现这些方法好像和人的学习类似,于是就将其取名为机器学习。
在比如我在网络上查阅神经网络的概念时,很多文章总是会从神经元等开始介绍。但是我想,设计神经网络的人看到不是一开始就把神经网络和神经元关联起来的,也并非根据生物学的神经网络而设计出了类神经网络,而是出现了这样的一个模型,甚至是“炼丹”出了这样一个模型之后,给这个模型取了一个好听的名字,比如为了拿去骗资金等等。
言归正传,什么是机器学习?机器学习就是让机器找一个函数,根据输入,这个函数会输出要得到的结果。比如下表是应用场景中设计到的函数的输入输出的举例。
| 应用场景 | 函数输入 | 函数输出 |
|---|---|---|
| 语音识别 | 音频 | 文字 |
| 图像识别 | 图片 | 类别 |
| α \alpha α Go | 当前棋局 | 下一手位置 |
各种各样的函数
| 函数输入 | 函数输出 | 应用场景举例 |
|---|---|---|
| 向量 | 数值 | 回归任务 |
| 向量 | 类别 | 分类任务(e.g.风铃分类) |
| 矩阵 | 类别 | 分类任务(e.g.图片分类) |
| 序列 | 类别 | 分类任务(e.g.speaker分类) |
| 序列 | 序列 | e.g.机器翻译 |
| 序列 | 矩阵 | e.g.人脸生成 |
机器学习的方法分类
监督学习(L1-L5)
收集大量带标签的训练资料训练模型。
注:标题中的L表示李老师课程的第几讲会讲相关内容,下同。
无监督学习(L6)
利用GAN(生成对抗网络)技术实现,只需收集大量输入输出,而不需要他们的成对关系,也不需要他们是相关的关系,训练后的机器就能自动实现输入到输出的转换。
自监督学习(L7)
在训练之前,模型先进行Pre-train,使之在新的任务上做得更好。Pre-train中使用的是没有标记的资料,得到Pre-trained模型,最终结果是在下游任务(真正要做的任务)上能得到好的结果。
强化学习(L12)
当人也不知道如何标注样本,但可以定义或判断好坏时,需要用到强化学习。
正确率之外的进阶目标
异常检测(L8)
机器能够发现异常的输入数据。
可解释AI(L9)
机器同时可以解释为什么得出这样的结果。
对模型的攻击(L10)
添加扰动后的对抗样本使得模型分类错误。
迁移学习(L11)
当测试样本与训练样本的分布不是类似的时候,模型依然要有很高的正确率,即领域自适应。
模型压缩(L13)
当计算资源等有限时,需要对模型进行压缩。
终身学习(L14)
无法训练一个学会所有技术、能够“统治”人类的机器。
元学习(L15)
让机器学习如何学习。机器从大量任务中自己发明新的算法进行训练。可以达到只用少量标注的样本就能进行学习。
机器学习基本概念介绍
机器学习的三大任务
回归
函数的输出是一个数值(标量)。
分类
函数的输出是一个设定好的选项中的一个。
结构化学习(structured learning)
机器产生有结构的输出,如图片、文档
机器学习的三个步骤
给出一个带有未知参数的函数
比如模型为 y = b + w x y=b+wx y=b+wx,其中 x x x是特征, y y y是模型的预测值(注意这里的 y y y不是标签,标签是正确的数值),和特征相乘的未知参数 w w w是权重,最后加上的未知参数 b b b是偏置bias。
定义损失函数
比如定义Loss函数为 L ( b , w ) L(b,w) L(b,w),损失函数是关于模型中的未知参数的函数,损失函数表示模型预测值和真实值之间的差距。Loss函数可以选择为平均绝对值误差、平均平方误差、交叉熵( y y y是概率分布时)等,根据对具体任务的要求进行选择。Loss函数值越小表明参数越好。
最优化
找出使得Loss函数最小的未知参数。一般来说,用到的方法就是梯度下降法。
梯度下降法
- 随机选取初始参数 w 0 w^0 w0
- 计算 w w w在 w i w^i wi处对Loss函数的梯度 ∇ \nabla ∇
- 对模型参数进行更新 w i + 1 = w i − η ∇ w^{i+1}=w^i-\eta\nabla wi+1=wi−η∇(每一次更新,参数的变化由学习率和偏导(梯度值)两方面决定)。
注:关于梯度和偏导数的关系,在此处,梯度是各个维度上的偏导数(标量)构成的向量,在一维情况下,可以认为偏导数和梯度是等价的。
说明:从理论上来说,梯度下降法可能会有仅仅是收敛到局部最优解的问题,不过李老师说在实际中不是问题(原因之后解释)。
超参数
包括学习率在内的需要自己设置的参数叫做超参数。
对模型进行修改
对模型进行的修改来自于对问题的理解(domain knowledge),用相对复杂的模型可以使得学习效果更好。
深度学习基本概念介绍
有弹性的模型
y = b + w x y=b+wx y=b+wx这种线性模型有很大的局限性,因此需要更加复杂的模型。
S型函数(sigmoid function)

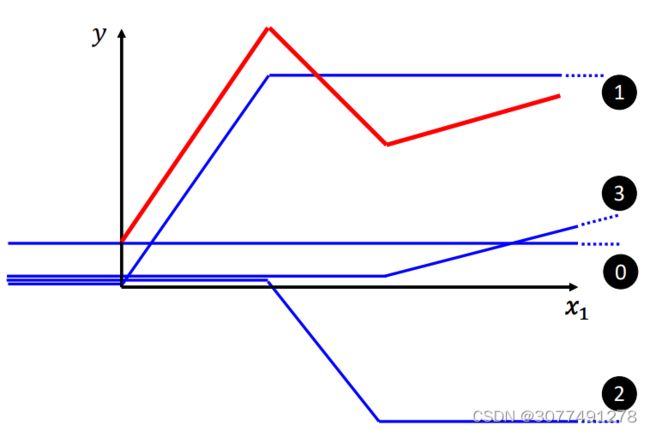
上图所示的sigmoid function是一种soft sigmoid function,而如果函数图像的中间也是直线则是hard sigmoid function。
用多个sigmoid function和一个常数项进行叠加可以逼近任何折线函数,而曲线函数又可以近似为无穷多个折线,故用多个sigmoid function和一个常数项进行叠加可以逼近任何函数。(即上图中的红线可以看成是其他蓝色线的叠加。)
由于hard sigmoid function的表达式比较难写,所以一般采用soft sigmoid function,比如 1 1 + e − ( w x + b ) \frac{1}{1+e^{-(wx+b)}} 1+e−(wx+b)1,简记为 s i g m o i d ( w x + b ) sigmoid(wx+b) sigmoid(wx+b)。
新的模型
故新的模型可以写作, y = b + ∑ i c i s i g m o i d ( w i x + b i ) y=b+\sum_ic_isigmoid(w_ix+b_i) y=b+∑icisigmoid(wix+bi),其中 b b b, c i c_i ci, w i , w_i, wi, b i b_i bi都是需要由训练得到的未知参数。当然这仅考虑了样本只有x这一个特征。
而当考虑更多特征时,应该是 y = b + ∑ j ∑ i c i s i g m o i d ( w i j x + b i ) y=b+\sum_j\sum_ic_isigmoid(w_{ij}x+b_i) y=b+∑j∑icisigmoid(wijx+bi),其中i是sigmoid函数的索引,j是特征的索引。
简写成线性代数的形式即为, y = b + c t δ ( W x + b ) y=b+c^t\delta(Wx+b) y=b+ctδ(Wx+b),其中 δ \delta δ表示多个sigmoid函数的作用。
新的损失函数
定义新的损失函数为 L ( θ ) L(\theta) L(θ),其中 θ \theta θ代表所有未知参数。
新的最优化
和前面的优化过程是类似的。
在实际训练过程中,往往会将训练数据分成很多批(batch),对每一个batch都会计算一个Loss函数,计算一个梯度并进行更新,对所有的batch完成一次计算叫做一轮(epoch)。
其他更多模型
也可以在模型中用其他S型函数。
ReLU函数

ReLU函数可以写为 c ∗ m a x ( 0 , w x + b ) c*max(0,wx+b) c∗max(0,wx+b)
两个ReLU函数进行叠加可以得到hard sigmoid function。
故新的模型可以写作, y = b + ∑ 2 i c i m a x ( 0 , w i x + b i ) y=b+\sum_{2i}c_imax(0,w_ix+b_i) y=b+∑2icimax(0,wix+bi),注意两个两个ReLU函数进行叠加得到一个hard sigmoid function,故和之前的模型相比需要 2 i 2i 2i个ReLU函数。
激活函数
sigmoid、ReLU等统称为激活函数。
用多个激活函数进行叠加训练
将每一次的激活函数结果 a a a继续作为下一个 x x x输入到另一个参数不同的激活函数中,即多层的神经网络,即深度学习。
当然如果网络的层数过多也会出现过拟合的问题,应该选择在测试集上而非训练集上表现得更好的模型作为合适的模型。