这一篇讨论统计学中,关于样本以及它的统计量的相关特性,重点是样本的均值和方差的相关问题。
统计量的期望值
假设我们有一个随机变量 \( X \),符合某种概率分布,整体的数学期望值和方差为:
$$ E(X) = \mu \\ D(X) = \sigma^2 $$
然而整体的期望值和方差通常都是未知的,所以我们采取抽样的方式,用样本的 统计量 来估计它们,这符合我们的直觉;
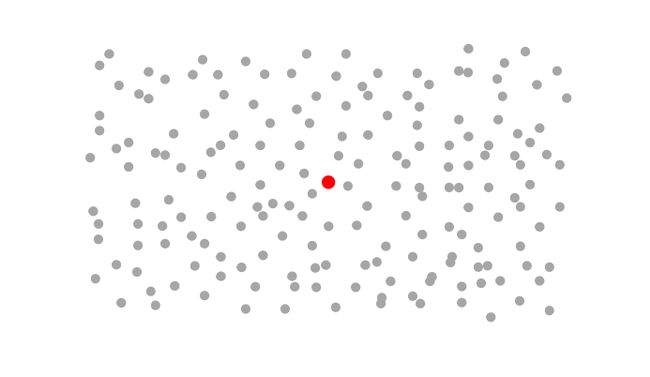
例如我们有一个随机变量 \( X \) 的分布,我们把它以一个图的形式展现:
它的整体期望值位于图中的红点,当然这个红点在哪里我们实际上不知道,但它是客观存在的,它的计算公式为:
$$ \mu = {1 \over N}\sum X_i $$
\( N \) 为原始数据的总量,通常 \( N \) 非常大(以至于无穷大),所以我们不可能计算上面的式子,所以说我们并不知道红点实际在哪里;
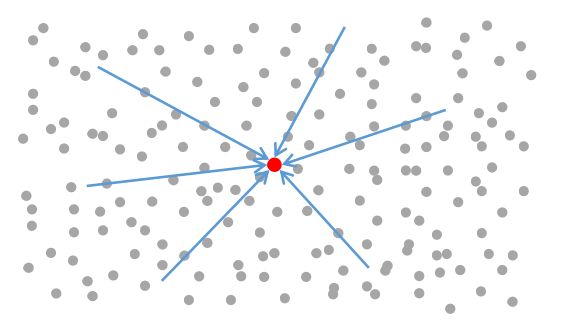
因此我们用 采样 的方法,每次只取出有限的 \( n \) 个值作为样本,即图中的一个个圆圈;计算这批样本的均值,即为每个圆圈中的绿色点,它的计算公式为:
$$ \overline{X} = {1 \over n} \sum {X_i} $$
当我们进行无数次这样的采样试验(画圈),得到无数个绿点,那么这些绿点的平均值等于原始数据的期望值,也就是红点;
也就是说有如下结论:样本均值的期望值,等于原始分布的期望值,即:
$$ E(\overline{X}) = E(X) =\mu $$
上面写了这么多,好像在说一件直观上很显而易见的事情;然而这是数学,即使它似乎是显而易见的,我们最好还是从数学上证明:
$$ \begin{align} E(\overline{X})&=E({1 \over n}\sum {X_i})\\ & ={1 \over n}E(\sum {X_i})\\ & ={1 \over n}[E(X_1)+...+E(X_n)]\\ & ={1 \over n}(n\mu) =\mu \end{align} $$
给出上述证明的目的,是为了引出后面的内容,我想要说明一个问题:统计学中有些似乎很直观、很显然的结论,其实并不能想当然,如果没有严格的数学证明支持,还是需要三思。
例如我们考虑下面的期望值:
$$ E(X^2) $$
即 \( X^2 \) 的期望值,它是否等于原始期望值 \( \mu \) 的平方 \( \mu^2 \)?
答案显然是否定的,例如考虑一个很简单的随机变量 \( X \) 的分布,它只有 3 和 5 两个取值,概率各占 0.5,那么它的原始期望值为:
$$ \mu = 3 \cdot 0.5 + 5 \cdot 0.5 = 4 $$
然而:
$$ E(X^2) = {3^2\cdot0.5+5^2\cdot0.5} = 17 \neq \mu^2 $$
它并不等于原始期望值 \( 4^2 =16 \),而是比它大;
更直白的,这在代数上是很简单的原理:平方平均值 >= 算数平均值
$$ {{a^2 + b^2}\over{2}} \geq ({{a + b}\over 2})^2 $$
因此我们得到一个结论:
$$ E(X^2) \geq \mu^2 $$
那 \( X^2 \) 的期望值究竟等于多少呢?它实际上等于(原始期望值的平方 + 方差):
$$ E(X^2) = \mu^2 + \sigma^2 $$
这也可以由数学公式推导出来,这里就不赘述了,你可以自己去翻概率统计的书;
样本方差
上面讨论了样本平均值,以及 \( X \) 平方,下面讨论一个更复杂的量:方差 \( \sigma^2 \);和期望值 \( \mu \) 一样,通常原始数据的方差我们也是未知的,我们需要使用样本去估计它;
上面我们计算过 \( n \) 个样本的平均值:
$$ \overline{X} = {1 \over n}\sum X_i $$
上面已经给出过证明,它的期望值,是等于原始变量 \( X \) 的期望值的,即:
$$ E(\overline{X}) = E(X) =\mu $$
也就是说我们可以使用样本的均值,来估计原始数据的期望值,这在统计学上叫做 无偏估计;在样本均值这个例子上,这好像是显而易见的;
然而如果计算 \( n \) 个样本的方差:
$$ {1 \over n}\sum ({X_i - \overline{X}})^2 $$
我们是不是也可以用它来无偏地估计整体的方差 \( \sigma^2 \) 呢?答案是否定的,也就是说:
$$ E\,[{1 \over n}\sum ({X_i - \overline{X}})^2] \neq \sigma^2 $$
如果你看过了关于上面 \( X \) 的平方的期望值的计算,应该能大概看出一个问题,就是关于 \( X \) 的比较复杂的统计量(非线性的,例如平方,方差等)的数据分布,是不能想当然的;
事实上,上面计算的 \( n \) 个样本的方差,它的期望值比原始方差通常要小一点,也就是说这个估计值是偏小的,它 低估 了真正的方差;真正准确的估计值,应该除以 \( n-1 \),而不是 \( n \):
$$ {1 \over n-1}\sum ({X_i - \overline{X}})^2 $$
这才是统计学上所说的 样本方差 的严格定义,它的数学期望值,等于原始分布 \( X \) 的方差:
$$ E\,[{1 \over n-1}\sum ({X_i - \overline{X}})^2] = \sigma^2 $$
这也是困扰很多初学者的一个很神奇的结论:为什么是 \( n-1 \)?
关于这个结论的公式的数学推导,我想很多地方都能找到,这里我仍然尝试给出一种直观的认识。
整体的方差,计算公式为:
$$ \sigma^2 = {1 \over N}\sum ({x_i - \mu})^2 $$
\( N \) 为原始数据的总量;上面的计算结果,其实就是所有灰点到红点的距离的平方平均值,这个很好理解;
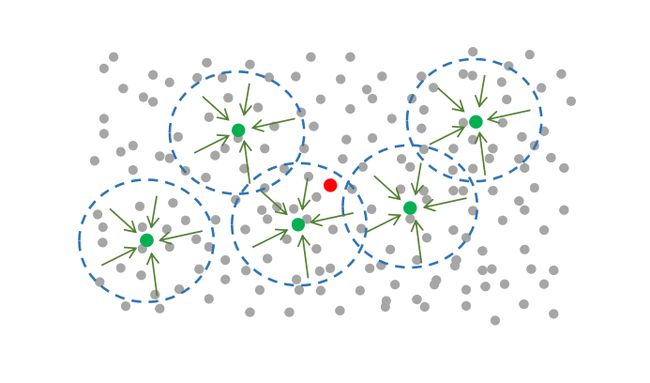
通常 \( N \) 非常大(以至于无穷大),并且我们也不知道整体的均值是多少,所以我们不可能计算上面的式子;因此我们仍然用采样的方法,每次只取出有限的 \( n \) 个值作为样本:
每个圆圈即为每次的采样范围,每次都采样 \( n \) 个点,绿色点为每一批样本的平均值,即:
$$ \overline{X} = {1 \over n}\sum X_i $$
如果通过下面的公式计算样本方差:
$$ {1 \over n}\sum ({X_i - \overline{X}})^2 $$
它计算的是每个圆圈中所有灰色点到绿色点的距离的平方平均值;
但是实际上,真正的原始数据的准确方差,应该使用灰色点到红色点的距离来计算,也就是这样:
$$ {1 \over n}\sum ({X_i - \mu})^2 $$
但问题是红色点是未知的,所以我们每次计算时使用的不是原始期望值 \( \mu \) ,而是样本平均值 \( \overline X \),即用绿色点来代替红色点;这就导致,我们使用的平均值(绿色点)本身其实就是离原始期望值(红色点)有偏差的,用它计算出来的方差,它当然也是有偏差的。
那它是偏大还是偏小呢?从图中直观地就能看出,它 每次 都是偏小的。圆圈中的点是采样数据,绿色点是它们的均值(或者说中心点),显然比红色点离它们本身更近;当然这只是图上的直观感受,从代数上来说,一堆数据,到它们中心点的平方和,比到其它任何点的平方和都要小。
正是因为采样数据计算出来的方差,每次都是偏小的,所以整体来看,我们即使进行无数次这样的采样试验,最后计算出来的方差的期望值,肯定也是偏小的。注意这里非常强调一个问题,即 每次 采样计算都是偏小的,这样整体算出来的期望值才是偏小的。
这就回到了一开始的问题,为什么用样本的方差来估计整体方差是有偏差的,并且是偏小的:
$$ {1 \over n}\sum ({X_i - \overline{X}})^2 $$
真正准确的估计,需要将 \( n \) 换成 \( n-1 \):
$$ {1 \over n-1}\sum ({X_i - \overline{X}})^2 $$
至于为什么是 \( n-1 \),这需要公式推导,这里就不做详细证明了,请去教科书上找一下吧。