大力飞砖之 Java 字符串（中-中（KMP&DP））

前言

主要在记录一下一些关于字符串的问题。
最近蓝桥杯在即，任重道远呀！！！

KMP

首先，作为java程序员还是幸运的，因为java内置的String里面所提供的的contains 等查找算法是一个复合算法，也就是说里面实现了一套kmp，或者是其他优秀的算法。

但是，题目往往不这样搞，例如。

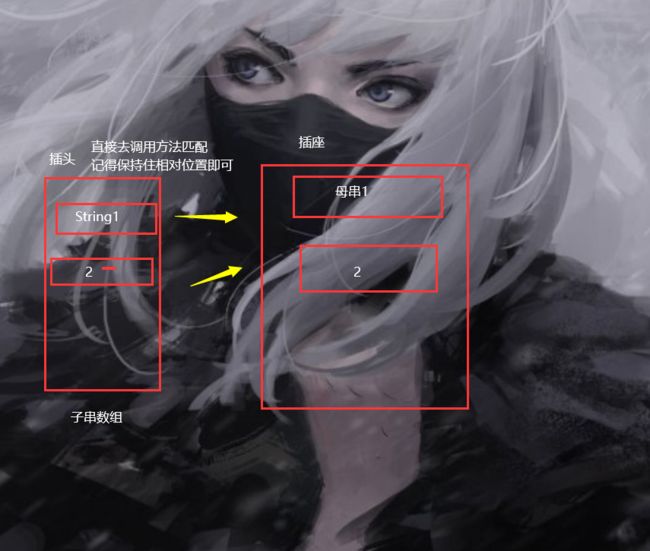
这个很明显是一个匹配问题，相当于字符串匹配，只不过人家是二维的。当然咱们这里还是可以投机取巧的。因为输入的其实是个字符串嘛，把每一行当做那个String，只需要记录出那个String的数组结构，和插头的结构，那么我不就可以直接调用String内置的函数了嘛。

当然这里是 投机的方法。

主要我们还是需要掌握那个 KMP 的，寒假的时候 我特意去再看了看，现在好久没用忘了，刚好回忆一下。

KMP 要素

想要实现KMP 算法，这个最主要的其实有两个玩意，一个是，咱们的对比规则，还有一个是咱们的next数组。

所以只要掌握了，这两个，那么KMP就写出来了，想要写出next数组又需要了解那个对比规则。知道了这些之后，完整的kmp就写出来了 。

对比规则

这个其实和暴力 的规则类似，区别就是，我们往前回退的时候（子串）是通过一个叫next数组的东西来回退到指定的位置的。这样一来，一旦匹配失败，那么子串里面的指针就不需要直接从头开始了，而是在某一个指定的位置，这样一来我们的算法就变得高效了起来。

i 指向的是咱们的母串
j 是指向子串
时间复杂度为O(n)

详细解释我们到后面再来，这个主要是啥是知道发挥大作用的是咱们的next数组

对比的核心代码如下：

      for (int i = 0, j = 0; i < n; i++) {
            while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
                j = next[j - 1];//有冲突
            }
            if (haystack.charAt(i) == needle.charAt(j)) {
                j++;
            }
            if (j == m) {
                return i - m + 1;
            }
        }
        return -1;

生产next数组

整个KMP 最神奇的部分就是如何生产next数组。这个数组是怎么样设置的。怎么样生产的。

这里我先把代码放出来。

needle 是咱们的子串，仔细看代码你会发现什么玩意！这个代码咋和咱们对比的代码那么像，只不过是“母串”和子串都是同一个
当然其实还有有点区别的，只是写起来很像。

        int[] next = new int[m];
        for (int i = 1, j = 0; i < m; i++) {
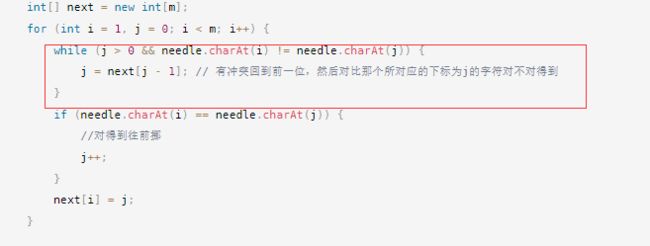
            while (j > 0 && needle.charAt(i) != needle.charAt(j)) {
                j = next[j - 1]; // 有冲突回到前一位，然后对比那个所对应的下标为j的字符对不对得到
            }
            if (needle.charAt(i) == needle.charAt(j)) {
            	//对得到往前挪
                j++;
            }
            next[i] = j;
        }

其实生产next数组就是这样的。

KMP 省事，其实是因为啥，其实是因为next数组知道，在子串里面前面有些字母是重复的，前面的字符没有必要去对比，所以这样一来嘿嘿，就省事了。

next 数组含义

这里我先不扯前缀，后缀了，没有太大意义，看了下面的图你就明白了。我就只需要记住一件事情。首先我们已经知道了KMP匹配的流程。一旦出现不匹配，i 指针在哪继续，j 指针不会回到起点，而是回到一个特殊的位置，例如这样的情况。

OK ，现在我们已经彻底懂了，我们的next数组到底用过干啥，就是因为在j当前对不到的时候，意味啥，意味j-1前面的都是对的到的，在母串i位置的时候对不到而已，而且如果在j个位置的左边，例如 j-1,j-2 和最前面的1 2 位置都是一样的，又意味着（我们假设从1开始）对于i-1,i-2而已和子串的1 2 位置是一定相同的，这样一来我只需要从子串的3这个位置去和i那个位置继续匹配。

前后缀

在理解清楚到咱们的这个next数组的作用之后，问题来到了我们怎么求出这样的数组。那么这个时候就需要扯到前后缀了。

对于一个字符串

a a b a a c
前缀是指包含第一个字符串不包含最后一个字符，的子串例如对于上面这个字符串他的前缀字符串有
a
a a
a a b
a a b a
a a b a a

那么后缀也是，除去第一个字符的，那么就有

c
a c
a a c
b a a c
a b a a c

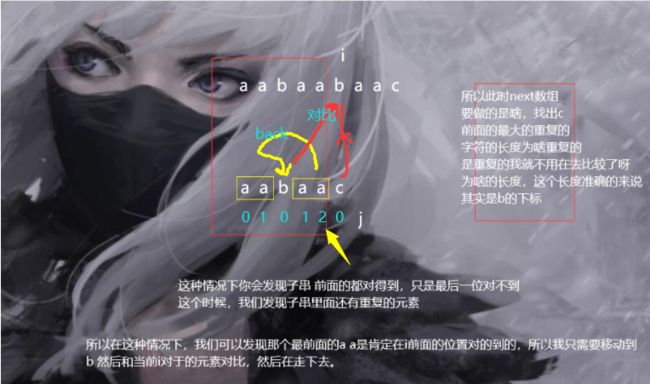
这个时候呀，你发现，最长的相等的前后缀是啥不就aa么，长度是2如果下标从0开始就找到了b这个时候咱们不就造出next数组了么
所以通过前后缀就知道了长度。

于是求出
a -->0
a a -->1 : a
a a b --> 0
a a b a --> 1:a
…

求取next数组

开始

=知道了前后缀，咱们就好办 了，我们就可以模拟这个过程嘛，我们从搞出 aa 开始
对于a来说，显然直接是0

我们模拟一遍我们一次就把 aa 搞定了
之后你还发现一个小细节，那个j不仅是前缀的下标，还是对应的长度。为什么，想想前面我说为啥我们要的是长度。

中间过程

接下来我们主要把目光放在这个部分,巧妙的地方开始了。

next 存的啥，是 i 长度的子串的最长的公共前缀。

我们下来看看求取这个 a a b

此时 i = 2
j = 1
a b 不相等
j = next[j-1] 也就是 next[0] 也就是 0
此时你发现这个 如果下面的是前缀的话，为啥，那个是从1开始的。其实这个也是个技巧，也是整个实现比较巧妙的地方。
后缀是加在后面的，前缀是加在最前面的，从上次的最长前缀开始去和和最长后缀的字符去比，这样我们就能压缩时间，也就是这样一个策略。

前后缀扩张，如果扩张成功 j++
如果扩张失败进入循环，也就是 最坏情况下我去看看 j-1 的这个最长后缀行不行，如果还不行再退也就是原来的j-2 此时的j-1
那么这里也一定程度上体现了dp思想，不过变种地有点厉害。

整合

接下来就是如何使用咱们的next数组了。

我们来看看上面的例子里面生产的next长啥样。

长这个样子：

怎么用，回到这个图呀

ok，最后 咱们在看看完整代码

public class KMP {

    public static void main(String[] args) {
        System.out.println(strStr("aabaabaac", "aabaac"));
    }

    public static int strStr(String haystack, String needle) {
        int n = haystack.length(), m = needle.length();
        if (m == 0) {
            return 0;
        }
        int[] next = new int[m];


        for (int i = 1, j = 0; i < m; i++) {
            while (j > 0 && needle.charAt(i) != needle.charAt(j)) {
                j = next[j - 1]; // 有冲突回到前一位，然后对比那个所对应的下标为j的字符对不对得到
            }
            if (needle.charAt(i) == needle.charAt(j)) {
                //对得到往前挪
                j++;
            }
            next[i] = j;
        }



        for (int i = 0, j = 0; i < n; i++) {
            while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
                j = next[j - 1];//有冲突
            }
            if (haystack.charAt(i) == needle.charAt(j)) {
                j++;
            }
            if (j == m) {
                return i - m + 1;
            }
        }
        return -1;
    }
}

当然对于咱们java组，咱们直接

dp例题

这个咋说呢，来都来了来一个和字符串相关的题目，刚好要和next有点像来。

题目

解题

抓住一个细节，以谁结尾，这种题目如果你想顺着推，那么我建议你DFS，如果你逆着推那么你就是dp，当然也有反过来的。例如

如果你想从1–》2021那么恭喜你，直接按照反过来的策略dp，如果你是正向，那么DFS吧（下面给出这个的代码，当然也要有一定策略）

   public static void f(int n){
        if(n==1){
            minCount = Math.min(minCount,current-1);
            return;
        }

        current++;
        if((n&1)==1){
            n/=2;
            f(n);
        }else {
            if(isT(n+1)){
                f(n+1);

            }else {
                f(n-1);
            }
        }


    }

回到我们刚刚的题目，我们反过来，那么就是值看看，这个例如字母 b 以它结尾的个数，就可以了，因为如果是以c结尾的就会包含 b那么不就巧了吗，这个和j = next[j-1]有点像。
不过题目这里注意要有重复的字符的处理。

public class 模拟4 {


    public static void main(String[] args) {

        String s="tocyjkdzcieoiodfpbgcncsrjbhmugdnojjddhllnofawllbhfiadgdcdjstemphmnjihecoapdjjrprrqnhgccevdarufmliqijgihhfgdcmxvicfauachlifhafpdccfseflcdgjncadfclvfmadvrnaaahahndsikzssoywakgnfjjaihtniptwoulxbaeqkqhfwl";
        int N = s.length();
        int[] dp = new int[N];

        for(int i=0;i<N;i++)dp[i]=1;
        for(int i=1;i<N;i++)
        {
            for(int j=0;j<i;j++)
            {
                if(s.charAt(i)>s.charAt(j))
                {
                    dp[i]+=dp[j];
                }
                else if(s.charAt(i)==s.charAt(j))
                {
                    dp[i]=0;//相等不加
                }
            }
        }

        int ans=0;
        for(int i=0;i<N;i++)
        {
            ans+=dp[i];
        }
        System.out.println(ans);

    }
}

总结

今天先这样吧，对于蓝桥杯我只能尽力垂死挣扎，没办法，事情很多，不是只有一个竞赛要搞，不过算法确实是一件值得坚持的事情。在大学，在该奋斗的年纪里面，我们必须全力以赴，想想，大学的妹子迟早要分，陪伴你的只有你付出了汗水得到的知识和成就，这也是我坚持日更博文的原因之一。