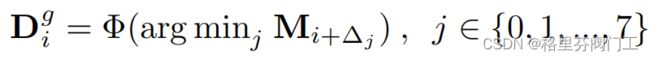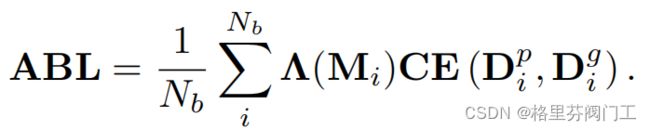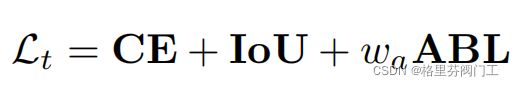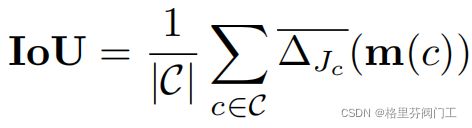粗读Active Boundary Loss for Semantic Segmentation

        本文通过让一个损失函数关注边界相关的信息，来提高在边界处的分割效果。整个思路麻烦且不直观，我直接讲方法吧。

        第一步，将GT中边界部分设为0，然后运算distance transform函数，让其他非0的像素计算自己距离最近的0的曼哈顿距离（好怪哦，bushi），得到一个大小为H*W，成员为整数的矩阵。

        第二步，让模型输出一个预测图P，大小为C*H*W，C为类别数量，每个通道对应一个类的物体的分割结果。然后，根据这个预测图计算B

        B的计算方式是从右上角开始，计算每一个点与它周围两个点的关系，具体的两个点是往下移一格与往左移一格的点（所以不用计算下沿和右边框上的的点）。所以这里的i，j实际上都是有两个数字的坐标值。因为预测图有C个通道，那么每个像素可以转化为一个长度为C的向量。计算两个向量的KL散度，如果散度差较大，那么就认为i点为边界点。

        作者用了自适应的方式调整阈值，凭经验，令边界点数量大约占总像素数量的1/100，因为大多数图像的GT中，边界像素数大概为总像素数的1/100。

        B的大小为H*W，成员为0或1。

        第三步，将B膨胀一格，即B中原本为1的格子周围8个格子的像素也视为1。

        然后遍历B，对所有为1的格子计算

        argmin的意思是获得：令后面的函数最小时的自变量的值。例如f(x^2)=x^2-4x-1，那么argmin f(x)=2，因为x=2时函数最小。

        这个式子中自变量为j，i实际上为坐标值，Δ是一个数组，数组成员是坐标值偏移，具体来说为∆ = {{1, 0}, {−1, 0}, {0, −1}, {0, 1}, {−1, 1}, {1, 1}, {−1, −1}, {1, −1}}。因此靠着argmin，可以找到预测的边界实际上应该往哪个方向偏移，因为M是计算像素点与实际边界的距离的结果，M越小说明j周围的那个点离边界更近。

        因为j是一个数，而为了后面的函数计算，要为8维向量，因此将j转化为一个长度为8的one-hot向量，并放入的位置i处，例如j=0，那么相应的向量为{1,0,0,0,0,0,0,0}。 

        最后计算。之前的g代表groud-truth，而p就代表predicted。的计算简单粗暴，就是计算i周围8个点，每个点于自己的KL散度的占比。 同样，只有计算了Dg的点才会计算Dp

        通过两个D，即可计算损失函数

        Nb为预测边界点数，即在计算B时值为1的点的数目。那个标志像刺客信条的函数计算公式如下

        x为i点在M上的值。θ为阈值，定为了20。这样离真实边界越远的预测边界影响越大，但不会过大导致其他错误预测的边界点的影响被盖过去。

        为了让损失函数越小，每一个点都要扩大与真实边界方向的点的KL散度，缩小与其他点的KL散度。毕竟Dp可以视为这个损失函数的GT，而Dp中只有边界方向的值为1，其余的为0。通过这个损失函数，预测出来的概率图P，同类别之间的点会尽可能分布相同，但与边界方向的点就会尽量不同，哪怕边界方向的点和自己是同类。

虽然以往我都是把模型框架示意图防最前面，但本文方法实在复杂，示意图初看完全不明白啥意思，但结合上文流程，示意图立马简单易懂了

        把local distance map视作Dg一部分，local probability map视作Dp一部分，便能明白这个损失函数在干啥了。

        最终损失函数为

 

        C为类别数，m(c)为预测c类错误数组，ΔJc是Jaccard loss，而这涉及到另一篇我还不了解的论文了。