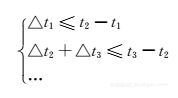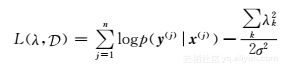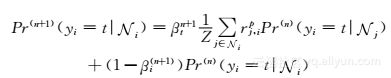《移动数据挖掘》—— 2.2 缺失数据补全

本节书摘来自华章出版社《移动数据挖掘》一 书中的第2章，第2.2节，作者连德富 张富峥 王英子 袁晶 谢幸，更多章节内容可以访问云栖社区“华章计算机”公众号查看。

2.2　缺失数据补全

前面提到过移动数据有多种类型，可能是人们携带智能设备收集的GPS轨迹数据，也可能是利用公交卡乘坐的公交车或地铁的信息，还可能是人们在移动社交网络中分享的地点访问信息，甚至是收集基站通信时留下的日志信息解析出的位置数据。在这些移动数据中，数据缺失是一种常见的现象。比如，当人们进入高楼大厦时，智能设备无法很好地与卫星定位系统进行通信，使得GPS可能很难对人们进行精确的定位。尽管结合基站定位或Wi-Fi定位，定位的方法得到了很大的改进，但是问题并没有得到彻底的解决。因而，人们通过智能设备获取的位置数据仍可能是缺失的或不精确的。再比如，人们在用公交卡乘坐公交车时，大部分仍然可能是只在上车的时候刷卡，从而无法获得人们下车的地点。再比如说，虽然人们愿意通过移动社交网络等分享自己的位置信息，但是涉及隐私地点、无趣地点的访问时 ，人们可能会故意地隐藏，这也会造成移动数据的缺失。而且现在人们分享位置信息的形式多种多样，可能是从数据库中选择出来的，也可能是人们自己创建的，但人们在创建的时候并没有填充相关的语义信息，这也会造成语义数据的缺失。最后，人们在打电话或发短信时，会通过与基站的通信留下自己的位置，但是人们只有很少一部分时间是用于打电话或发短信的，因而有大量时间的位置信息也是缺失的。针对这些缺失的情形，有些是可以通过技术手段解决的，有些却是无法通过技术手段解决的。在这些可以用技术手段解决的缺失问题中，有些可以通过时间序列中的值缺失解决方法来解决，有些可以通过矩阵填充的方法来解决，还有些可能需要根据实际情况运用数据挖掘的方法进行分析。下面将介绍两种重要的缺失数据补全解决方案。

2.2.1　公交卡的上下点补全

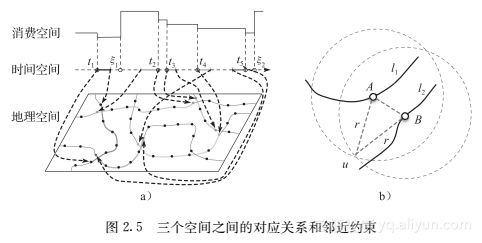
智能卡，比如信用卡、校园卡、公共交通卡，包含了丰富的人的行为信息。特别是记录了人的移动信息的智能公交卡，里面丰富的数据对于很多行业的人来说都是极具吸引力的，比如城市规划者和提供地点相关服务的从业人员。近些年基于智能公交卡数据的研究有很多，诸如行为建模和个性化推荐工作。但是由于许多智能系统的搭建都是以盈利为目的的，或者系统记录数据只是为了方便管理，记录的数据往往不够全面。比如单一票价的公交系统，一般就不会记录乘客上车和下车的站点，对于这种数据，如果能恢复出乘客完整的出行路线，将非常有利于后续的研究。在公交系统的数据中存在三种平行的数据空间：消费空间、时间空间和地理空间。图2.5a展示了三种不同的空间之间的对应关系。消费空间包括了卡的余额、充值金额和一次乘车行为的消费金额，卡的余额会在充值后上升，在乘车后下降，并且消费和充值行为都对应了时间空间里的一些点（如图2.5a所示）。在乘车过程中，乘客的地理移动和时间空间也是相互对应的，图2.5a中，时间空间中的实线表示乘车行为，虚线表示在这段时间里面乘客没有乘车。

除了有乘坐公交车的用途以外，很多智能公交卡还可以被用来乘坐出租车甚至去商场消费，使得公交系统记录的数据在消费空间上常常是不连续的。为了保证消费空间的连续性，需要将个人消费记录进行分割。

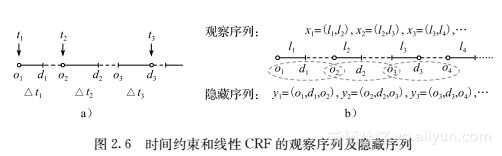
通过这样的分割算法，一个分割段中的消费记录就是连续的了。值得强调的是，这里的每个分割段中都可以包含很多天的数据。在一个分割段中，可以将乘客的行为定义成两种：行程内转移和行程外转移。定义2（行程内转移和行程外转移）　给定一个分割段S={l1,l2,…,lm}，其中li是一条从上车地点oi到下车地点di的公交行程，我们称oi→di是行程内转移，乘客在这期间的移动完全受公交的限制（顺着公交线路延伸），两个连续的行程之间的行为称为行程外转移，比如，di→oi+1。乘客在行程内和行程外的转移都具有很多种可能性，比如在一次乘车行为中，假设该条公交车线路有n个不同的站点，并且乘客的上车站和下车站不同，那么这次乘车就有n(n-1)种可能的转移。给行程内和行程外的行为加上在不同空间（消费空间、时间空间、地理空间）的限制，可以大大减小可能的转移数目。距离约束（对于行程外转移）　城市里人们的换乘距离往往是有上限的。如图2.5b所示，l1和l2是乘客u的两趟连续的公交行程，如果u只通过步行来完成l1和l2之间的换乘，那么可以认为这个距离不会超过某个范围。假设乘客u从A和B点出发的步行范围是两个以距离r为半径的圆形，分别以A和B点为圆心，那么通过三角不等式可以得出，A和B点的距离应该小于2r。在一次行程外行为中，满足距离约束的换乘站可以是0对（乘客可能通过别的交通方式从l1移动到l2，并且距离超过了2r），这种行程外转移的节点被称为漂移点，从漂移点将分割段分割成两个子段，这样每个分割段不仅在消费空间上是连续的，在地理空间上也是连续的。票价限制（对于行程内转移）　公交系统中通常有两种公交线路：阶梯票价线路和非阶梯票价线路。对于非阶梯票价线路，每次行程的票价都是固定的，而对于阶梯票价线路，票价则是根据上车和下车站点的距离来决定的，比如北京的阶梯票价计算方式为e=a+b·max(boarding-alighting-c,0)，其中e是票价，a、b、c是系统参数，对于不同的公交线路有不同的数值，这个公式说明当行程不大于c千米时，票价是a，否则每多1千米需要多付b元。实验中计算每次行程的可能票价，并且与乘客的真实消费相比较，可以大大减少可能的行程数目。时间约束（对于行程内和行程外转移）　如北京的公交系统，非阶梯票价线路会记录乘客的上车时间，阶梯票价线路会记录乘客的下车时间。虽然每段行程只记录一次时间，我们仍然可以用时间约束来过滤掉很多不可能的转移。用t1、t2、t3分别表示三段行程li=(oi，di)（i=1,2,3）的时间戳。如图2.6a所示，l1和l2是两条非阶梯票价线路，l3是一条阶梯票价线路。可以用距离和每段公路的限速来估计oi和di之间的最小时间△ti。那么图2.6a中的线路需要满足以下条件：

有约束的半监督CRF模型　条件随机场（CRFs）［53］在数据挖掘和机器学习领域中有着广泛的应用，特别是线性CRF模型，定义了由观察序列到隐藏序列的条件概率，构成了一个无向的图模型。事实上，给定了一个分割段的候选行程后，恢复数据的问题就转化成了在序列中对数据进行标记的问题了。具体来说，是先构造一个线性CRF模型：给定一个分割段S={l1，l2,…，lm}，用xi=(li，li+1)（对于i=1,2,…，m-1）来表示观察序列，也就是说，连续两条线路之间的行程外转移在CRF序列中被包含在一个节点中（如图2.6b所示，在这里一个节点表示两条线路），用yi=(yi1，yi2，y3i)表示一个行程内转移和紧接着的一个行程外转移的三元组(oi，di，oi+1)（i=1,2,…,m-1），序列y={y1,y2,…,ym-1}就是隐藏序列（也称标记序列）。对于标记数据足够多的CRF序列，通常使用EM算法或梯度法来训练对数似然函数

其中是训练序列，n是长度。对于标记数据不够多的模型，可以使用有约束的半监督CRF模型来解决问题。具体来说，给定一个约束方程G(y,x)和一个未标记的数据集，广义期望标准可以定义为

其中p(x)是数据集的经验分布，E［·］表示期望值，S是表示模型期望和目标期望之间的差值的得分函数。这个函数可以用梯度法来优化。

2.2.2　地点类别补全

根据参考文献［139］中提供的统计信息，在移动社交网络Whrrl和Foursquare中，大约有30％的地点是缺失语义信息的。语义信息对后续的挖掘具有重要的意义，因而，迫切需要对这些语义信息进行填充。填充的可行性来自于“具有类似语义的地点具有相似的模式”的发现，比如说大家去餐馆吃午饭的时间基本上都是中午。为此，叶懋（音译）等人在参考文献［139］中将填充问题归结为一个多标签分类问题，对每一个地点的每个类别标签，均采用二分类的算法进行分类。在分类器的特征中，作者提出利用地点的显性模式和相似地点的隐性相关性。显性模式是针对来自某个地点的所有访问数据得到的统计信息，比如访问时间分布、访问次数。由于带有不同语义标签的地点可能会有不同类型的时间分布，因而可以利用地点的时间分布来填充语义信息。举例来说，图2.7a和图2.7b给出了Whrrl数据上关于学校类地点和酒吧类地点在一个星期的不同天中的分布，以及餐馆和商店在一天的不同小时中的分布。可以看到酒吧类地点的访问时间更多地集中在周末，而学校类的地点则更多地分布在工作日中。同样，不同地点的访问频率也有所不同，比如说，对于个人来讲，医院的访问频率相较于餐馆来说要低很多。因而，地点的连续两次访问的时间间隔也是一个重要的指标。不过由于移动社交网络数据中的稀疏性，这个统计指标可能会有较大的偏差，甚至对于很多地点无法计算。为此，可以考虑用地点的总访问人数和单个用户的最大访问次数来进行替代。图2.7c和图2.7d给出了具有不同语义信息的地点的分布差异性。愿意和大家分享自己在医院的人是非常少的，但是愿意分享去餐馆就餐的用户却会很多。同样，对于常人来说，不可能每天都住在酒店；但是民以食为天，人们经常去餐馆便是可能的。

不过这些统计信息并没有刻画地点之间的相关性，使得缺乏足够访问信息的地点无法被很好地语义标注。因而，在本章中，作者提出利用相似地点的隐性相关性，将具有足够多访问历史地点的语义信息传播给缺乏足够访问信息的地点。相似地点的隐性相关性是通过地点的相似性网络来刻画的，相似性网络可以通过用户访问地点的规律性来构建。具体的做法是，它首先将所有用户的移动数据处理成用户地点的二部图，以及访问时间段地点的二部图。其中用户地点二部图中的连边代表用户访问过该地点，边的权重为用户对该地点的访问次数；而时间段地点二部图中的连边表示地点在这个时间段内被访问过，边的权重为所有用户在该时间段中访问该地点的总次数。在二部图中利用带重启动的随机游走［126］，可以估计从某个地点节点开始游走到其他地点节点的概率。特别地，从某个地点出发，要么沿着二部图中的边进行随机游走，或者从该地点节点重启动，直到收敛为止。假设对于任意的两个地点i和j，分别对时间段地点和用户地点二部图运用带重启动的随机游走获得的地点隐性相关性为rti,j和rui,j。这两个地点的隐性相关性通过线性加权的方法进行结合，得到地点i和j的最终的隐性相关性rpi,j=ηrui,j+(1-η)rti,j。这里的η是一个平衡系数。基于地点的隐性相关性，可构建相关地点的有向图网络。特别地，为每个地点选取最相似的k个地点，每个地点和k个最近邻的地点形成相应的连边，边权不变。给定这种相关地点的相似性网络，可以通过类似于半监督学习的方法来进行语义标签的预测。特别地，某个地点属于某个语义类别的概率是正比于与它相似地点的对应类别的概率的加权和。假设i表示为地点i的k最近邻地点，那么Pr(yi=ti)就表示从地点i的k最近邻地点推测地点i的类别为t的概率。这个概率是通过如下公式进行迭代估计的

即每次地点语义类别估计概率都是在上一次的概率估计基础上更新的，其中Z=∑j∈irpj,i是归一化项，Pr(n)(yi=ti)表示Pr(yi=ti)的第n次迭代的估计。β(n+1)t=β(n)tα=β(0)tαn+1是加权系数，其中β(0)t为一个在0和1之间的常量，而α为小于1的非负衰减因子。而且由于不同语义类型的地点受k近邻的影响也有所不同，所以β(0)t是与类别相关的，使得具有较小β(0)t值的语义类别地点受近邻的影响较大，而具有较大β(0)t值的语义类别地点也受较不相似的地点的影响显著。在获得Pr(yi=ti)后，可以通过与统计指标结合的方法来获得最佳的地点语义信息补全。