线段树模板(不会有人还不会吧?比如我)
文章目录
- 基础学习
-
- 题目大意
- 分析
- 线段树的基本思想
-
- 建树
- 查询区间和
- 修改一个数
- ACC代码
- 应用
-
- 分析
- 代码1(Y总写法)
- 代码2(myself)
基础学习
首先,讲得非常好的UP猪(链接点着里~)
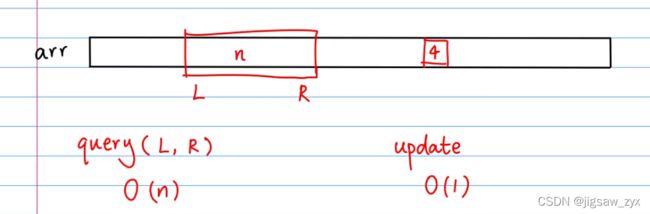
题目大意
要求查找一个区间内的和,和修改一个数
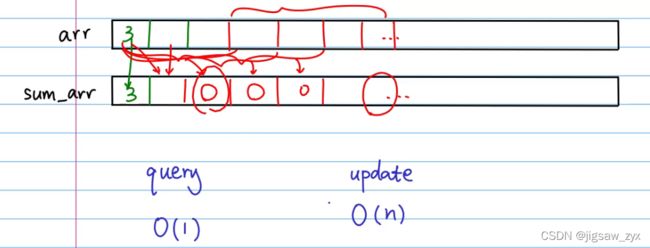
分析
如果是用遍历或者前缀和的思想,无论如何总有一个操作是O(n)的时间复杂度,这时候就需要我们寻找另外的办法降低复杂度
线段树的基本思想
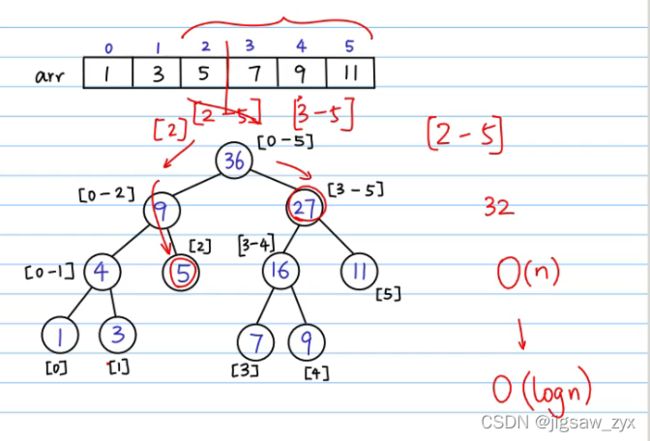
建树
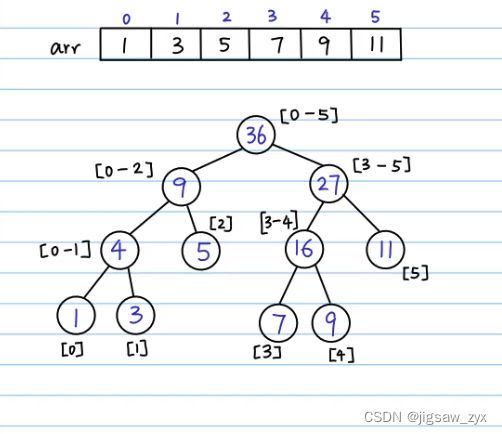
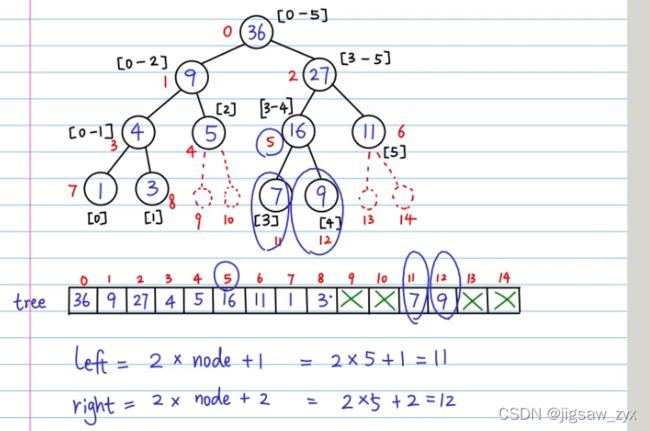
由于这里存树是用完全二叉树存树,在理想情况下,N个叶节点的满二叉树有N+N/2+N/4+N/8…+2+1=2N+1个节点,因为在此存储方式下,最后一层产生了空余,所以我们保存数组的长度要不小于4N,这样才能保证不越界。
代码实现
const int N=1086;
int a[N]={1,3,5,7,9,11};
int siz=6,tree[N*4];
//建树
void build(int node,int start,int end){
if(start==end){
tree[node]=a[start];
return ;
}
int left=2*node+1,right=node*2+2;
int mid=(start+end)>>1;
build(left,start,mid);
build(right,mid+1,end);
tree[node]=tree[left]+tree[right];
}
查询区间和
//查询:查询l到r的和
int query(int node,int start,int end,int l,int r){
if(start==end){
return tree[node];
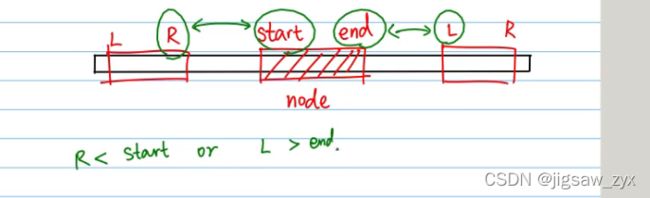
}else if(end<l||r<start){//不在计算范围之内
return 0;
}else if(l<=start&&end<=r){//l<=start
return tree[node];
}
int mid=(start+end)>>1;
int left=2*node+1,right=node*2+2;
int suml=query(left,start,mid,l,r),sumr=query(right,mid+1,end,l,r);
return suml+sumr;
}
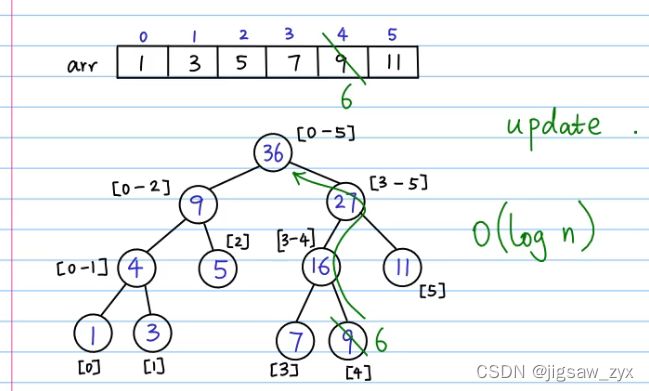
修改一个数
//修改一个值 :把数组里面第k个数改为val
void update(int node,int start,int end,int k,int val){
if(start==end){
tree[node]=val;
a[k]=val;
return ;
}
int mid=(start+end)>>1;
int left=2*node+1,right=node*2+2;
if(k>=start&&k<=mid) update(node*2+1,start,mid,k,val);
else update(node*2+2,mid+1,end,k,val);
tree[node]=tree[left]+tree[right];
}
ACC代码
#include
return tree[node];
}
int mid=(start+end)>>1;
int left=2*node+1,right=node*2+2;
int suml=query(left,start,mid,l,r),sumr=query(right,mid+1,end,l,r);
return suml+sumr;
}
int main(){
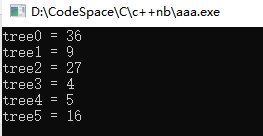
build(0,0,siz-1);
cout<<"建树:"<<endl;
for(int i=0;i<siz;i++){
cout<<"tree"<<i<<" = "<<tree[i]<<endl;
}
cout<<endl;
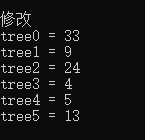
cout<<"修改"<<endl;
update(0,0,siz-1,4,6);
for(int i=0;i<siz;i++){
cout<<"tree"<<i<<" = "<<tree[i]<<endl;
}
cout<<endl;
cout<<"查询:"<<endl;
int ans=query(0,0,siz-1,2,5);
cout<<"ans="<<ans<<endl;
return 0;
}
应用
分析
将求和变成了求最大值,维护线段树的节点即可
代码1(Y总写法)
#include代码2(myself)
#includeif (start==end){
tree[node]=val;
return ;
}
int mid=start+end>>1;
int l=node*2,r=node*2+1;
if(k<=mid&&k>=start) update(l,start,mid,k,val);
else update(r,mid+1,end,k,val);
tree[node]=max(tree[l],tree[r]);
}
//查询区间内的最大值
int query(int node,int start,int end,int l,int r){
if(l<=start&&end<=r) return tree[node];
else if(start==end) return tree[node];
else if(end<l||start>r) return 0;
int mid=start+end>>1;
int maxl=query(node*2,start,mid,l,r),maxr=query(node*2+1,mid+1,end,l,r);
return max(maxl,maxr);
}
int main(){
int n=0,last=0;
cin>>m>>p;
//初始化,树上的节点全部都是0,有m个叶节点的满二叉树
memset(tree,0,sizeof tree);
int x;
char op;
int v=m;
while(v--){
cin>>op>>x;
if(op=='Q'){
last=query(1,1,m,n-x+1,n);
cout<<last<<endl;
}else{
update(1,1,m,n+1,(last+x)%p);
n++;
//for(int i=1;i<=m*4;i++) cout<<"tree"<
}
}
return 0;
}