# 2017年蓝桥杯省赛cc++本科B组试题
2017年蓝桥杯省赛c/c++本科B组试题
第一题:购物单
问题
小明刚刚找到工作,老板人很好,只是老板夫人很爱购物。老板忙的时候经常让小明帮忙到商场代为购物。小明很厌烦,但又不好推辞。
这不,XX大促销又来了!老板夫人开出了长长的购物单,都是有打折优惠的。
小明也有个怪癖,不到万不得已,从不刷卡,直接现金搞定。
现在小明很心烦,请你帮他计算一下,需要从取款机上取多少现金,才能搞定这次购物。
取款机只能提供100元面额的纸币。小明想尽可能少取些现金,够用就行了。
你的任务是计算出,小明最少需要取多少现金。
以下是让人头疼的购物单,为了保护隐私,物品名称被隐藏了。
**** 180.90 88折
**** 10.25 65折
**** 56.14 9折
**** 104.65 9折
**** 100.30 88折
**** 297.15 半价
**** 26.75 65折
**** 130.62 半价
**** 240.28 58折
**** 270.62 8折
**** 115.87 88折
**** 247.34 95折
**** 73.21 9折
**** 101.00 半价
**** 79.54 半价
**** 278.44 7折
**** 199.26 半价
**** 12.97 9折
**** 166.30 78折
**** 125.50 58折
**** 84.98 9折
**** 113.35 68折
**** 166.57 半价
**** 42.56 9折
**** 81.90 95折
**** 131.78 8折
**** 255.89 78折
**** 109.17 9折
**** 146.69 68折
**** 139.33 65折
**** 141.16 78折
**** 154.74 8折
**** 59.42 8折
**** 85.44 68折
**** 293.70 88折
**** 261.79 65折
**** 11.30 88折
**** 268.27 58折
**** 128.29 88折
**** 251.03 8折
**** 208.39 75折
**** 128.88 75折
**** 62.06 9折
**** 225.87 75折
**** 12.89 75折
**** 34.28 75折
**** 62.16 58折
**** 129.12 半价
**** 218.37 半价
**** 289.69 8折
需要说明的是,88折指的是按标价的88%计算,而8折是按80%计算,余者类推。
特别地,半价是按50%计算。
请提交小明要从取款机上提取的金额,单位是元。
答案是一个整数,类似4300的样子,结尾必然是00,不要填写任何多余的内容。
特别提醒:不许携带计算器入场,也不能打开手机
笔记
说实话这题真让人感觉烦,50个数据太烦了,将清单复制到txt文本里面,利用Ctrl+H替换掉这些字符和折扣。预处理好数据之后用代码计算即可!
答案:5200
第二题:等差数列
问题
2,3,5,7,11,13,…是素数序列。
类似:7,37,67,97,127,157 这样完全由素数组成的等差数列,叫等差素数数列。
上边的数列公差为30,长度为6。
2004年,格林与华人陶哲轩合作证明了:存在任意长度的素数等差数列。
这是数论领域一项惊人的成果!
有这一理论为基础,请你借助手中的计算机,满怀信心地搜索:
长度为10的等差素数列,其公差最小值是多少?
注意:需要提交的是一个整数,不要填写任何多余的内容和说明文字。
代码
#include
#include
#include
#include
#include
using namespace std;
int main()
{
bool b[10001];
memset(b, 1, sizeof(b));
b[1] = 0;
for (int i = 2; i <= 10000; i++)
for (int j = 2; j <= sqrt(i); j++)
if (!(i % j)) b[i] = 0;
for (int j = 1; j <= 1000; j ++ )
for (int i = 2; i <= 10000 - j * 9; i++)
{
bool yes = 1;
for (int k = 0; k <= 9; k++)
yes = yes && b[i + k * j];
if (yes) {
cout << j;
system("pause");
return 0;
}
}
}
第三题:承压计算
问题
X星球的高科技实验室中整齐地堆放着某批珍贵金属原料。
每块金属原料的外形、尺寸完全一致,但重量不同。
金属材料被严格地堆放成金字塔形。
其中的数字代表金属块的重量(计量单位较大)。
最下一层的X代表30台极高精度的电子秤。
假设每块原料的重量都十分精确地平均落在下方的两个金属块上,
最后,所有的金属块的重量都严格精确地平分落在最底层的电子秤上。
电子秤的计量单位很小,所以显示的数字很大。
工作人员发现,其中读数最小的电子秤的示数为:2086458231
请你推算出:读数最大的电子秤的示数为多少?
把每一块原料的重量平均分配到它地下的两块原料,最后枚举最底下的一排数据即可。
代码
#include
#include
#include
using namespace std;
int main()
{
fstream in("data.in");
double s[32][32], a, b;
memset(s, 0, sizeof(s));
for (int i = 1; i <= 29; i++)
{
for (int j = 1; j <= i; j++)
{
in >> s[i][j];
s[i][j] += (s[i - 1][j] / 2) + (s[i - 1][j - 1] / 2);
}
}
int i = 30;
for (int j = 1; j <= i; j++)
{
in >> s[i][j];
s[i][j] += (s[i - 1][j] / 2) + (s[i - 1][j - 1] / 2);
}
double mi = s[30][1], ma=s[30][1];
for (int i = 1; i <= 30; i++)
{
if (mi > s[30][i]) mi = s[30][i];
if (ma < s[30][i]) ma = s[30][i];
}
cout << mi << " " <<(long long)( ma * (((long long)2086458231) / mi));
system("pause");
return 0;
}
笔记
把每一块原料的重量平均分配到它地下的两块原料,最后枚举最底下的一排数据即可。
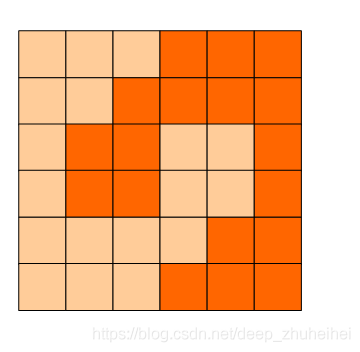
第四题:方格分割
问题
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。


代码
#include
#include
#include
#include
#include
#include
#include
#include 第五题:取数位
问题
求1个整数的第k位数字有很多种方法。
以下的方法就是一种。
对于题目中的测试数据,应该打印5。
请仔细分析源码,并补充划线部分所缺少的代码。
注意:只提交缺失的代码,不要填写任何已有内容或说明性的文字。
代码
#include
// 求x用10进制表示时的数位长度
int len(int x){
if(x<10) return 1;
return len(x/10)+1;
}
// 取x的第k位数字
int f(int x, int k){
if(len(x)-k==0) return x%10;
return f(x/10,k); //填空
}
int main()
{
int x = 23574;
printf("%d\n", f(x,3));
return 0;
}
第六题:最大公共子串
问题
最大公共子串长度问题就是:
求两个串的所有子串中能够匹配上的最大长度是多少。
比如:“abcdkkk” 和 “baabcdadabc”,
可以找到的最长的公共子串是"abcd",所以最大公共子串长度为4。
下面的程序是采用矩阵法进行求解的,这对串的规模不大的情况还是比较有效的解法。
请分析该解法的思路,并补全划线部分缺失的代码。
注意:只提交缺少的代码,不要提交已有的代码和符号。也不要提交说明性文字。
代码
#include
#include
#define N 256
int f(const char* s1, const char* s2)
{
int a[N][N];
int len1 = strlen(s1);
int len2 = strlen(s2);
int i,j;
memset(a,0,sizeof(int)*N*N);
int max = 0;
for(i=1; i<=len1; i++){
for(j=1; j<=len2; j++){
if(s1[i-1]==s2[j-1]) {
a[i][j] = a[i-1][j-1]+1;
if(a[i][j] > max) max = a[i][j];
}
}
}
return max;
}
int main()
{
printf("%d\n", f("abcdkkk", "baabcdadabc"));
return 0;
}
笔记
a[i][j]表示前一个字符串的前i位与后一个字符串的前j位的公共字符串长度
第七题:日期问题
问题
小明正在整理一批历史文献。这些历史文献中出现了很多日期。小明知道这些日期都在1960年1月1日至2059年12月31日。令小明头疼的是,这些日期采用的格式非常不统一,有采用年/月/日的,有采用月/日/年的,还有采用日/月/年的。更加麻烦的是,年份也都省略了前两位,使得文献上的一个日期,存在很多可能的日期与其对应。
比如02/03/04,可能是2002年03月04日、2004年02月03日或2004年03月02日。
给出一个文献上的日期,你能帮助小明判断有哪些可能的日期对其对应吗?
输入
一个日期,格式是"AA/BB/CC"。 (0 <= A, B, C <= 9)
输出
输出若干个不相同的日期,每个日期一行,格式是"yyyy-MM-dd"。多个日期按从早到晚排列。
样例输入
02/03/04
样例输出
2002-03-04
2004-02-03
2004-03-02
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
代码
#include
#include
#include
#include
#include
#include
using namespace std;
string s;
struct ppp{
long year, mouth, day;
} e[100];
long tot;
const int od[13] = { 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 };
int get_char(char c)
{
return int(c) - int('0');
}
int cmp(const void *i, const void *j)
{
struct ppp *a = (struct ppp *) i;
struct ppp *b = (struct ppp *) j;
if (a->year != b->year)return a->year > b->year;
if (a->mouth != b->mouth) return a->mouth > b->mouth;
return a->day > b->day;
}
bool pdd(int year, int mouth, int day)
{
int x = 0;
if (!(year % 400) || !(year % 4)) x = 1;
if (mouth > 12) return 0;
if (mouth == 2 && day <= od[2] + x) return 1;
if (day > od[mouth]) return 0;
return 1;
}
void pd(int year, int mouth, int day)
{
if (year < 60) year = 2000 + year;
else year = 1900 + year;
if (pdd(year, mouth, day))
{
++tot;
e[tot].year = year;
e[tot].mouth = mouth;
e[tot].day = day;
}
}
int main()
{
cin >> s;
int x, y, z;
x = get_char(s[0]) * 10 + get_char(s[1]);
y = get_char(s[3]) * 10 + get_char(s[4]);
z = get_char(s[6]) * 10 + get_char(s[7]);
tot = -1;
if (y <= z) swap(y, z);
if (x <= y) swap(x, y);
if (y <= z) swap(y, z);
if (x == y && x == z) pd(x, y, z);
if (x == y && x != z)
{
pd(x, y, z);
pd(z, x, y);
pd(x, z, y);
}
if (z == y && x != z)
{
pd(x, y, z);
pd(z, x, y);
pd(z, y, x);
}
if (x != y && x != z && y != z)
{
pd(x, y, z); pd(x, z, y);
pd(y, x, z); pd(y, z, x);
pd(z, x, y); pd(z, y, x);
}
qsort(e, tot + 1, sizeof(ppp), cmp);
for (int i = 0; i <= tot; i++)
cout << e[i].year << "/" << e[i].mouth << "/" << e[i].day << endl;
system("pause");
}
第八题:包子凑数
问题
小明几乎每天早晨都会在一家包子铺吃早餐。他发现这家包子铺有N种蒸笼,其中第i种蒸笼恰好能放Ai个包子。每种蒸笼都有非常多笼,可以认为是无限笼。
每当有顾客想买X个包子,卖包子的大叔就会迅速选出若干笼包子来,使得这若干笼中恰好一共有X个包子。比如一共有3种蒸笼,分别能放3、4和5个包子。当顾客想买11个包子时,大叔就会选2笼3个的再加1笼5个的(也可能选出1笼3个的再加2笼4个的)。
当然有时包子大叔无论如何也凑不出顾客想买的数量。比如一共有3种蒸笼,分别能放4、5和6个包子。而顾客想买7个包子时,大叔就凑不出来了。
小明想知道一共有多少种数目是包子大叔凑不出来的。
输入
第一行包含一个整数N。(1 <= N <= 100)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100)
输出
一个整数代表答案。如果凑不出的数目有无限多个,输出INF。
例如,
输入:
2
4
5
程序应该输出:
6
再例如,
输入:
2
4
6
程序应该输出:
INF
样例解释:
对于样例1,凑不出的数目包括:1, 2, 3, 6, 7, 11。
对于样例2,所有奇数都凑不出来,所以有无限多个。
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <???>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
代码
#include
#include
#include
#include
#include
#include
#include
#include 第九题:分巧克力
问题
儿童节那天有K位小朋友到小明家做客。小明拿出了珍藏的巧克力招待小朋友们。
小明一共有N块巧克力,其中第i块是Hi x Wi的方格组成的长方形。
为了公平起见,小明需要从这 N 块巧克力中切出K块巧克力分给小朋友们。切出的巧克力需要满足:
1. 形状是正方形,边长是整数
2. 大小相同
例如一块6x5的巧克力可以切出6块2x2的巧克力或者2块3x3的巧克力。
当然小朋友们都希望得到的巧克力尽可能大,你能帮小Hi计算出最大的边长是多少么?
输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含两个整数Hi和Wi。(1 <= Hi, Wi <= 100000)
输入保证每位小朋友至少能获得一块1x1的巧克力。
输出
输出切出的正方形巧克力最大可能的边长。
样例输入:
2 10
6 5
5 6
样例输出:
2
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <???>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
代码
#include
#include
#include
#include
#include
#define zy 100002
using namespace std ;
long n , k , h[ zy ] , w[ zy ] , ans ;
bool pd( long t )
{
long tot = 0 ;
for ( int i = 1 ; i <= n ; i ++ )
tot += ( h[ i ] / t ) * ( w[ i ] / t );
if ( tot >= k ) return 1 ;
return 0 ;
}
void find( long head , long last )
{
if ( head > last ) return ;
long t = (last + head ) >> 1 ;
if ( pd( t ) )
{
ans = max( ans , t ) ;
find( t + 1 , last ) ;
}
else find( head , t - 1 ) ;
}
int main()
{
cin >> n >> k ;
for ( long i = 1 ; i <= n ; i ++ )
cin >> h[ i ]>> w[ i ] ;
ans = 1 ;
find( 1 , zy ) ;
cout << ans ;
return 0 ;
}
第十题:k倍区间
问题
给定一个长度为N的数列,A1, A2, … AN,如果其中一段连续的子序列Ai, Ai+1, … Aj(i <= j)之和是K的倍数,我们就称这个区间[i, j]是K倍区间。
你能求出数列中总共有多少个K倍区间吗?
输入
第一行包含两个整数N和K。(1 <= N, K <= 100000)
以下N行每行包含一个整数Ai。(1 <= Ai <= 100000)
输出
输出一个整数,代表K倍区间的数目。
例如,
输入:
5 2
1
2
3
4
5
程序应该输出:
6
资源约定:
峰值内存消耗(含虚拟机) < 256M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入…” 的多余内容。
注意:
main函数需要返回0;
只使用ANSI C/ANSI C++ 标准;
不要调用依赖于编译环境或操作系统的特殊函数。
所有依赖的函数必须明确地在源文件中 #include <???>
不能通过工程设置而省略常用头文件。
提交程序时,注意选择所期望的语言类型和编译器类型。
代码
#include
long long t[100010]={0};
long long a[100010]={0};
int main()
{
long long k,n;
scanf("%lld%lld",&n,&k);
int i;
for(i = 1; i<=n;i++)
scanf("%lld",&a[i]);
long long sum=0;
for(i=1;i<=n;i++)
a[i] = (a[i]+a[i-1])%k;
for(i=1;i<=n;i++)
sum+=(t[a[i]]++);
sum+=t[0];
printf("%lld\n",sum);
return 0;
}
笔记
首先统计前缀和sum[i] 表示A1+A2+…+Ai.所以对于任意一段区间[l,r]的和就是sum[r]-sum[l-1]。如果要保证这个区间和为K倍数就是:(sum[r]-sum[l-1])%k == 0.变形后就是:sum[r]%k==sum[l-1]%k,所以我们计算前缀和的时候顺带模K,然后统计前缀和中相同的数据就行了。复杂度O(n),注意数据可能会溢出!
